Engineering Physics: Unit I: Mechanics
Moment of inertia of continuous bodies (rigid bodies)
1. Moment of inertia of a thin uniform rod 2. Moment of inertia of thin ring (or hoop) 3. Moment of inertia of a thin circular disc 4. Moment of Inertia of Solid sphere 5. Moment of Inertia of a Solid cylinder
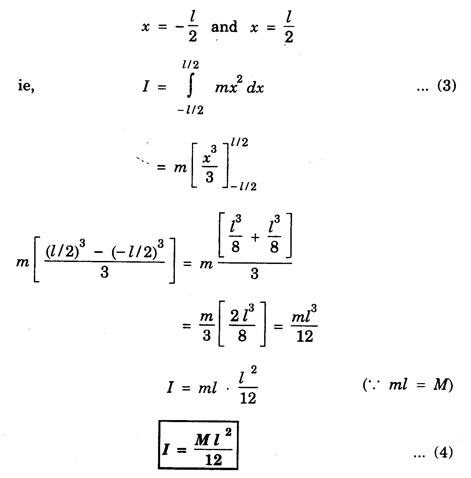
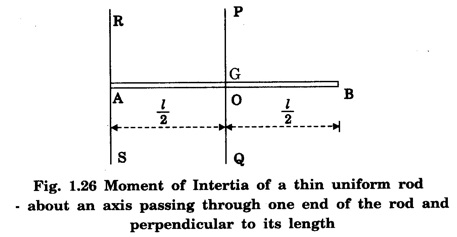
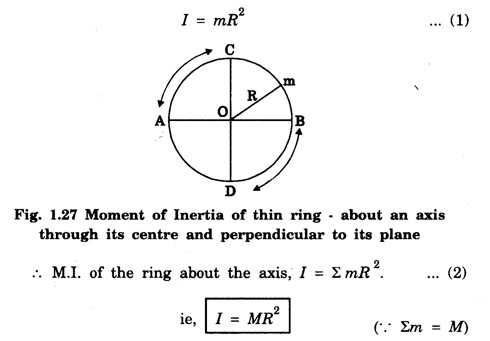
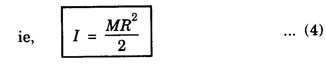
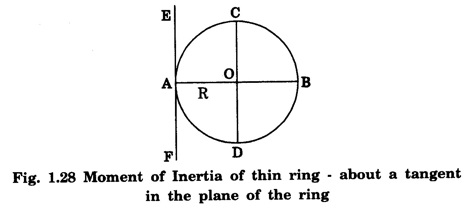
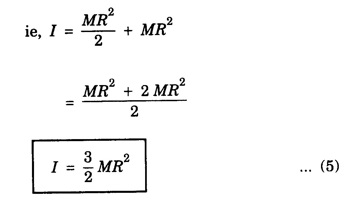
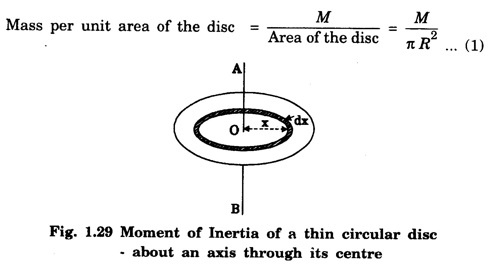
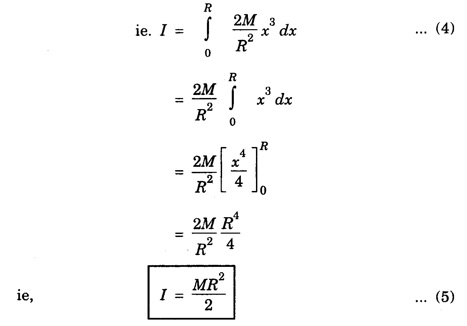
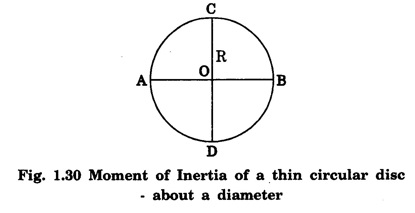
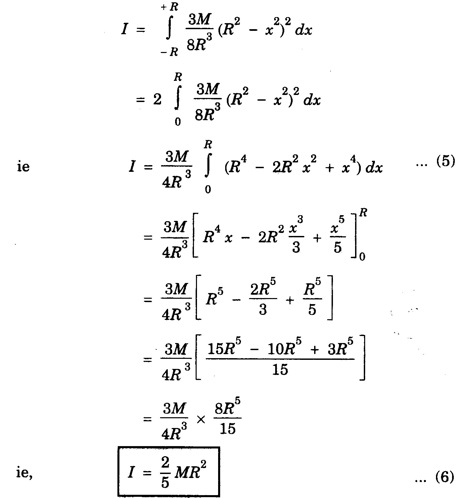
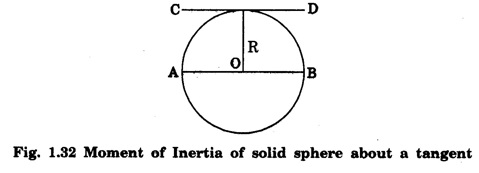
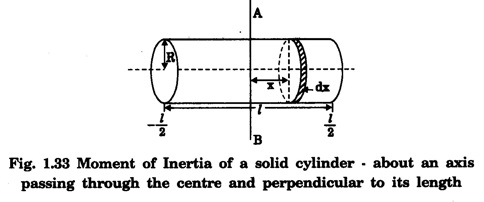
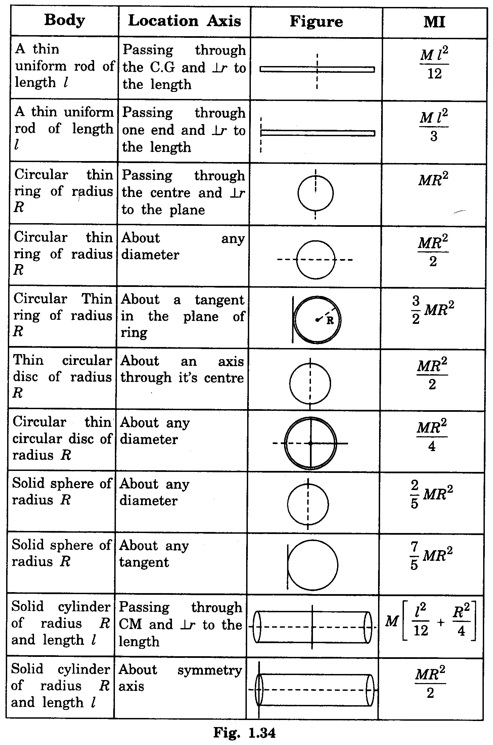
MOMENT OF INERTIA OF CONTINUOUS BODIES (RIGID BODIES) 1. Moment of inertia of a thin uniform rod (a) About an axis through its centre and perpendicular to its length Let AB be a thin uniform rod of length l and mass M. The rod is free to rotate about an axis PQ perpendicular to its length and passing through its centre O. (Fig. 1.25) Mass per unit length (linear density) of the rod, m = M/l ... (1) Consider a small element of length dx of the rod at a distance x, from O. Mass of the element = m . dx M.I. of this element about the axis PQ = mass × (distance)2. = mdx . x2 = mx2 dx ... (2) The rod AB is considered to be made up of a number of such small elements of length dx. Hence the moment of inertia I of the rod about the axis PQ is obtained by integrating the moments of inertia of all such elements lying between the limits (b) About an axis passing through one end of the rod and perpendicular to its length Let AB be a thin uniform rod of length l and mass M. O is its centre. As the rod is uniform, its centre and centre of gravity coincide. PQ is an axis passing through O and perpendicular to the length of the rod. (Fig. 1.26) M.I. of the rod about PQ = Ml2/12 ... (1) Let RS be an axis passing through one end A and perpendicular to the length of the rod. Let I be the moment of inertia of the rod about the axis RS. By the theorem of parallel axes, M.I. of the rod about the axis RS = M.I. of the rod about the axis PQ passing through the centre of gravity + Mass × square of the distance of the axis from the C.G. Therefore, 2. Moment of inertia of thin ring (or hoop) (a) About an axis through its centre and perpendicular to its plane Let M be the mass and R, the radius of a thin circular ring with centre O. Let I be the moment of inertia of the ring about an axis passing through O and perpendicular to the plane of the ring Consider a particle of mass m of the ring. Its moment of inertia about the axis passing through O and perpendicular to the plane of the ring is (b) About a diameter AB and CD represent two mutually perpendicular diameters of the ring. The moment of inertia of the ring about any diameter is the same. (Fig, 1.27) Let I be the moment of inertia about AB. Then about CD also, the moment of inertia is I. By the theorem of perpendicular axes, the moment of inertia of the ring about an axis passing through O and perpendicular to its plane is equal to the sum of the moments of inertia about two mutually perpendicular axes in the plane of the ring. i.e., Iz = Ix + Iy ... (3) But, Iz = MR2 and Ix = Iy = I .: MR2 = I + I or, 2I = MR2 (c) About a tangent in the plane of the ring Let EF be a tangent to the ring at A, in the plane of the ring and also it is parallel to the diameter CD. Let I be the moment of inertia of the ring about the tangent EF. By parallel axis theorem, M.I. about EF = M.I. about CD. + Mass × square of the distance OA (a) About an axis through its centre and perpendicular to its plane Let M be the mass and R, the radius of a thin circular disc. The disc is free to rotate about an axis AB passing through its centre O, and perpendicular to its plane. Consider a narrow circular strip of the disc with centre O and radius x. Let dx be its radial width. Area of the strip = 2 π x dx. Moment of inertia of this circular strip about the axis AB The circular disc is considered to be made up of a large number of such narrow strips, concentric with O and radii ranging from 0 to R. Hence, the moment of inertia I of the disc about the axis AB is obtained by integrating the above expression between limits x = 0 and x = R. (b) About a diameter Let AB and CD be two perpendicular diameters of the disc. The moment of inertia of the disc about any diameter is the same as that about any other diameter. Hence the moments of inertia about AB and CD are equal. Let each of them be I. The moment of inertia of the disc about an axis, through the centre and perpendicular to the plane of the disc is = MR2/2 ... (6) Therefore, by the theorem of perpendicular axes, Iz = Ix + Iy ... (7) But, Iz = MR2/2 and Ix = Iy + I MR2/2 = I + I MR2/2 = 2I I = MR2/2 × 2 (a) About a diameter Let M be the mass of a uniform solid sphere of radius R and centre O. The sphere is free to rotate about its diameter AB. Mass per unit volume (density) of the sphere Consider a thin circular slice (elemental volume) of the sphere at a distance x from O. Let dx be the thickness of the slice. This slice is a thin uniform disc. The radius of this disc is given by y2 = (R2 – x2) (⸪ R2 = x2 + y2) Area of this disc = πy2 = π (R2 – x2) (⸪ y2 = R2 - x2) Volume of the disc = Area × thickness = π (R2 – x2) dx ……….(2) The sphere is considered to be made up of large number of such discs, with x varying from -R to + R. Hence, the moment of inertia I of the sphere is obtained by integrating the above expression between limits x = -R and x = + R. ie, Moment of inertia of the solid sphere about a diameter. (b) About a tangent A tangent drawn to the sphere at any point is parallel to one of its diameter. The distance between the tangent and the diameter is R, the radius of the sphere. (Fig. 1.32) By the theorem of parallel axes, the M.I. of the sphere about the tangent CD, I = M.I. of the sphere about a parallel axis AB passing through the centre + Mass of the sphere × Square of the distance between the axes. (a) About an axis passing through the centre and perpendicular to its length Let M be the mass of a solid cylinder of length l and radius R. The cylinder is free to rotate about an axis. AB passing through the centre and perpendicular to its length. Mass per unit length (linear density) of the cylinder, m = M/l ... (1) The cylinder is imaged to be divided into a large number of thin circular discs with their plane at right angles to the length of the cylinder. Consider one such circular disc of thickness dx at a distance x from the axis AB. Mass of the disc = m dx Moment of inertia of this disc about its own diameter. ∴ Moment of inertia of this disc about the axis AB, parallel to the diameter = Moment of inertia about the diameter + Mass × square of the distance between the axes. (using parallel axes theorem). Therefore, the moment of inertia of the solid cylinder about axis AB, is obtained by integrating the above expression between limits x = -l/2 and x = + l /2. ∴ M.I. of the cylinder about AB, (b) About the axis of the cylinder A solid cylinder is considered to be a thick circular disc. It is composed of a large number of thin circular discs placed one above the other. Let each such elementary disc be of mass m and radius R, equal to the radius of the cylinder. The moment of inertia of each such disc about an axis passing through its centre and perpendicular to its plane = mR2/2 ... (8) ∴ M.I. of the solid cylinder about its axis = ∑ mR2/2 where M is the mass of the cylinder. Moment of Inertia of Certain Rigid Bodies of mass M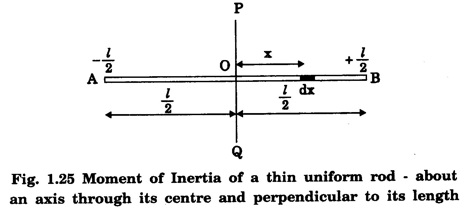
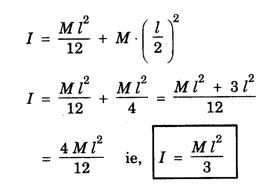
3. Moment of inertia of a thin circular disc
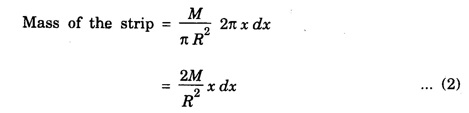
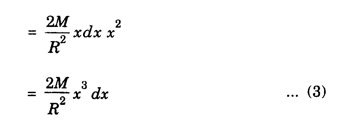
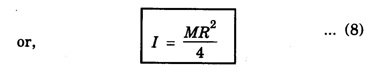
4. Moment of Inertia of Solid sphere
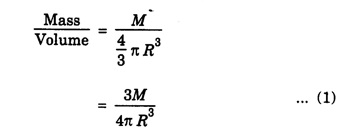

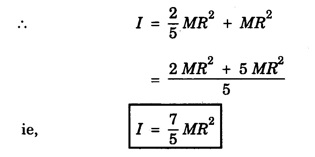
5. Moment of Inertia of a Solid cylinder
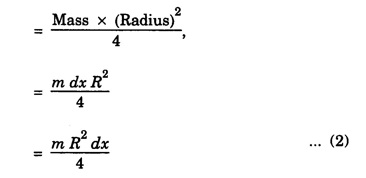
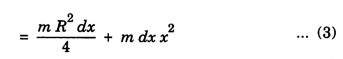


Engineering Physics: Unit I: Mechanics : Tag: : - Moment of inertia of continuous bodies (rigid bodies)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
