Engineering Physics: Unit I: Mechanics
Moment of inertia of a diatomic molecule
A diatomic molecule, in its stable equilibrium position consists two atoms that are at a distance 'R' apart. The distance 'R' is called the bond length between the two atoms.
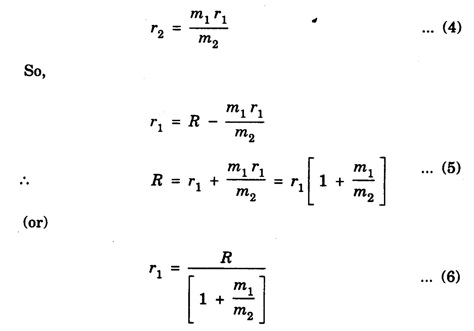
MOMENT OF INERTIA OF A DIATOMIC MOLECULE A diatomic molecule, in its stable equilibrium position consists two atoms that are at a distance 'R' apart. The distance 'R' is called the bond length between the two atoms. Presently we can consider that it consists of two tiny spheres at either end of a thin weightless rigid rod, as shown in fig. 1.35. This kind of arrangement can be called as rigid rotor. Let ‘C" be the center of mass of the molecule and r1 and r2, the respective distances of the two atoms from it. Then r1 + r2 = R .... (1) and m1 r1 = m2 r2 .... (2) where m1 and m2 are the masses of two atoms respectively. From eqn.(1), r1 = R – r2 .... (3) and from eqn.(2), Now, the moment of inertia of the molecule (i.e., of the two atoms) about an axis passing through the center of mass "C" and perpendicular to the bond is given as I = m1 r12 = m2 r22 .... (7) So, I = m1 r1. r1 + m1 r1. r2, [ ⸪ From eqn.(2)] I = m1 r1 (r1 + r2), (or) by using eqn.(1), Substituting eqn.(6) in eqn.(8) gives So where In fig. 1.36, K = R, which is called radius of gyration, so moment of inertia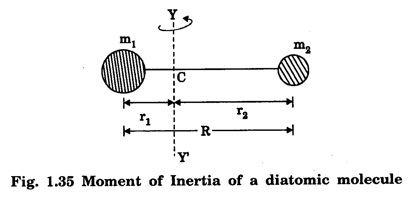

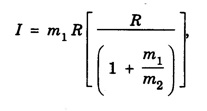
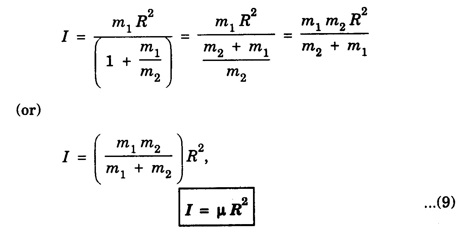
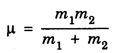 is called as reduced mass of the molecule. Thus the figure 1.35 can also be redrawn as
is called as reduced mass of the molecule. Thus the figure 1.35 can also be redrawn as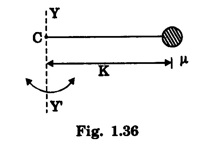

Engineering Physics: Unit I: Mechanics : Tag: : - Moment of inertia of a diatomic molecule
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
