Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies
Moment of Force about a Point
Extend the line of action of given force and draw perpendicular to it from the point about which moment is required.
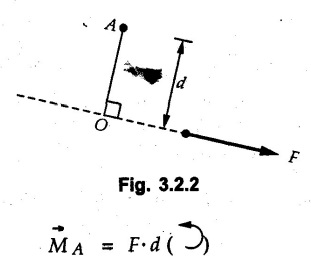
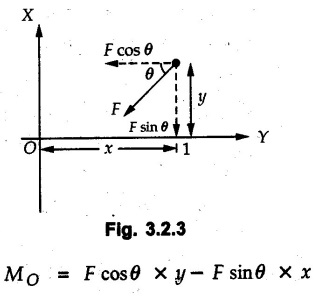
Moment of Force about a Point • Moment of force Where • Note that the moment is a vector quantity which is directed perpendicular to the plane containing • Its direction can be obtained by either using right handed screw rule or right hand rule as discussed in section 1.7.2. • Consider a force Seen from the tip of • The magnitude of moment is • If a perpendicular AB is drawn from A on the line of action of i.e., the magnitude of moment is product of the magnitude of force and perpendicular distance of the force from point A. • For a system of coplanar forces, the direction of moment vector will be either outward from the plane or into the plane. • Throughout this book, the outward direction of • Moment of force can be calculated in the following two ways: 1. Extend the line of action of given force and draw perpendicular to it from the point about which moment is required. The magnitude of moment will be the product of magnitude of force and the perpendicular distance. e.g. the moment of force F shown in Fig. 3.2.2 about A is, 2. Resolve the force into two mutually perpendicular components at a point on its line of action where the pependicular distances are known for the components. Then find the total moment due to the two components. e.g., for the force F shown in Fig. 3.2.3., the moment of force F about O is This method involves the use of Varignon's theorem which is discussed in the next article. • Note that the X-component of F is towards left but the corresponding term in the moment equation is positive as it produces anticlockwise moment. • While writing moment, the sign convention is not for force. It is for the clockwise or anticlockwise moment that it produces. • Sometimes, it is desired to produce maximum moment with a given amount of force. For example, while opening a wooden door which has got jammed in rainy season. As, M = r Fsin θ, for maximum M, r and sin θ have to be maximum i.e. force has to be applied at maximum distance from the point about which moment is taken and (sinθ)max = 1 hence θ = 90°, i.e., force has to be applied perpendicular to the line joining the point about which moment is taken and the point of application of force. • To produce some given moment with minimum force, the conditions remain same.. for minimum F, r and sin θ have to be maximum. Note: If force is passing through a point about which moment is taken, then its moment about that point is zero. Refer Fig. 3.2.4. • Geometrically, force is represented by directed line segment, the length of the line being proportional to the magnitude of force. • Consider a force • The moment about point C is given by MC = F d. Where d is the perpendicular distance of force • If a triangle is drawn by joining end points of the line segment AB to point C, the area of the triangle so formed is • Thus moment of force = Twice the area of triangle formed by joining the end points of force to the point about which moment is taken.![]() about a point A is given by
about a point A is given by
![]() is a vector drawn from A to any point on the line of action of
is a vector drawn from A to any point on the line of action of ![]() .
.![]() and
and ![]() .
.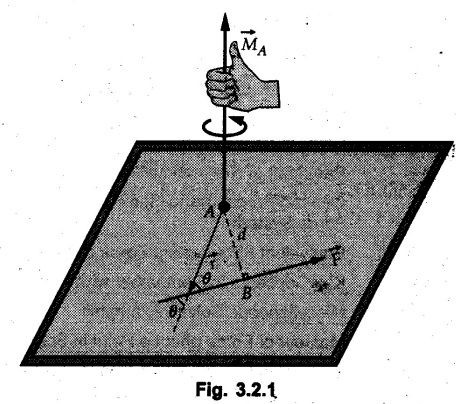
![]() in the plane of paper as shown in Fig. 3.2.1. Its moment about A will be outward (in the direction of the thumb) as shown using right hand rule. The curl of the fingers around the moment axis at A gives the sense of rotation of the moment.
in the plane of paper as shown in Fig. 3.2.1. Its moment about A will be outward (in the direction of the thumb) as shown using right hand rule. The curl of the fingers around the moment axis at A gives the sense of rotation of the moment. ![]() towards A, this sense of rotation is anticlockwise.
towards A, this sense of rotation is anticlockwise.
![]() as shown in Fig. 3.2.1. then,
as shown in Fig. 3.2.1. then,
![]() corresponding to anticlockwise sense of rotation will be taken as positive and the clockwise sense of rotation as negative.
corresponding to anticlockwise sense of rotation will be taken as positive and the clockwise sense of rotation as negative. 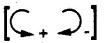
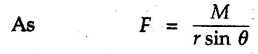
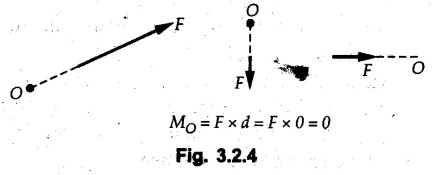
Geometrical interpretation of moment
![]() represented by the line segment AB as shown in Fig. 3.2.5.
represented by the line segment AB as shown in Fig. 3.2.5.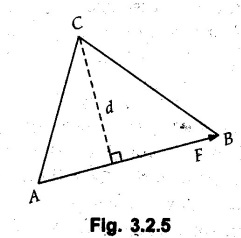
![]() from C.
from C.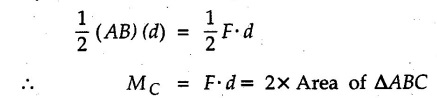
Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies : Tag: : - Moment of Force about a Point
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
