Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Mixtures of Real Gases
with Solved Example Problems | Thermodynamics
To analyze the mixture of real gases, PVT relationships are used. According to Dalton law, the pressure of mixture of gases is equal to the sum of the pressure of individual gas.
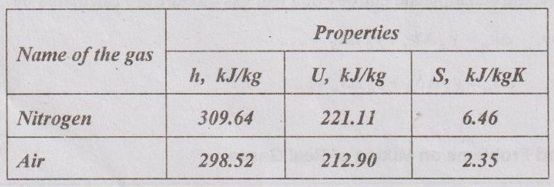
MIXTURES OF REAL GASES To analyze the mixture of real gases, PVT relationships are used. According to Dalton law, the pressure of mixture of gases is equal to the sum of the pressure of individual gas. For example, if three gases are mixed, the mixture pressure becomes pm = pA + pB + pC ……..(5.135) But, the pressure is the function of mole fraction, temperature and volume of gases. So, equation (5.135) can be written as pm = pA (NA, Tm, Vm) + pB (NB, Tm, Vm) + pC (NC, Tm, Vm) where Tm and Vm = Temperature and volume of mixture gas respectively NA, NB and NC = Number of moles of gas A, B and C respectively. Similarly, volume can be written as Vm = VA (NA, pm, Tm) + VB (NB, pm, Tm) + VC (NC, pm, Tm) Here, volume is the function of number of moles, pressure and temperature. It is the second method based on Amagat's law The third method uses a compressibility factor to analyse the mixture of real gases. It is given by Problem 5.9 Air contains 21% of oxygen and 79% of nitrogen by volume. Determine the molecular weight of air, R and density at STP. Given data: The pressure and temperature at STP are 1 bar and 23°C respectively. Solution: Problem 5.10 An ideal gas mixture consisting of 3 kg of air and 7 kg of nitrogen at a temperature of 25°C occupies a volume of 1 m3. Determine the partial pressure, specific volume, specific enthalpy, specific internal energy and specific entropy of the mixture. Assume that air and nitrogen are ideal gases. Take R for air is 0.287 kJ/kgK and for nitrogen is 0.297 kJ/kgK. The other properties of air and nitrogen are given below. Given data: For air: Mass, ma = 3 kg Temperature, Ta =25°C + 273 = 298 K Volume, Va = 1 m3 Gas constant, Ra = 0.287 kJ/kgK Enthalpy, ha = 298.52 kJ/kg Internal energy, ua = 212.90 kJ/kg Entropy, Sa = 2.35 kJ/kgK For Nitrogen: Mass, mN2 = 7 kg Temperature, TN2 = 298 K Volume, VN2 = 1 m3 RN2 = 0.297 kJ/kgK hN2 = 309.64 kJ/kg uN2 = 221.11 kJ/kg sN2 = 6.46 kJ/kgK To find: h, u and s Solution: Problem 5.11 A mixture of ideal gases consists of 5 kg nitrogen and 10 kg of carbon dioxide at a pressure 250 kPa and a temperature of 25°C. Find the (i) mole fraction of each constituent (ii) equivalent molecular weight of the mixture (iii) equivalent gas constant of the mixture (iv) volume and density of the mixture and (v) Cp and Cv of the mixture. If the mixture is heated at constant volume to 50°C, find the change in internal energy, enthalpy and entropy of the mixture. Find the same properties of the mixture if the heating is carried out at constant pressure to 60°C. Take γ for N2 and CO2 as 1.4 and 1.286. Given data: mN2 = 5 kg mCO2 = 10 kg pm = 250 kPa Tm = 25°C = 25 + 273 = 298 K = T1 Case (i): Constant volume process, T2 = 50°C = 50 + 273 = 323 K Case (ii): Constant pressure process, T2 = 60°C = 60 + 273 = 333 K (i) If the mixture is heated at constant volume, (ii) If the mixture is heated at constant pressure, Problem 5.12 Find the increase in entropy when 5 kg of oxygen at 60°C are mixed with 7.5 kg of nitrogen at the same temperature. The initial pressure of each constituent is 103 kPa and is the same as that of mixture. Given data: Mass of oxygen, mo2 = 5 kg Temperature, To2 = TN2 = 60°C = 273 + 60 = 333 K Mass of nitrogen, mN2 = 7.5 kg Pressure, pm = 103 kPa To find: ΔS Solution: Problem 5.13 A vessel is divided into three compartments (a), (b) and (c) by two partitions. Part (a) contains oxygen and has a volume of 0.1 m3, (b) has a volume of 0.2 m3 and contains nitrogen, while (c) is 0.05 m3 and holds CO2. All three parts are at a pressure of 2 bar and a temperature of 13°C. When the partitions are removed and the gases mix, determine the change in entropy of each constituent, the final pressure in the vessel and the partial pressure of each gas. The vessel may be taken as being completely isolated from its surroundings. Given data: pm = 2 bar = 200 kPa Tm = To2 = Tco2 = TN2 = 13°C = 273 + 13 = 286 K Vo2 = 0.1 m3 VN2 = 0.2 m3 Vco2 = 0.05 m3 Solution: Problem 5.14 A closed rigid cylinder is divided by a diaphragm into two equal compartments, each of volume 0.1 m3. Each compartment contains air at a temperature of 20°C. The pressure in one compartment is 2.5 MPa and in the other compartment is 1 MPa. The diaphragm is ruptured so that the air in both the compartments mixes to bring the pressure to a uniform value throughout the cylinder which is insulated. Find the net change of entropy for the mixing process. Given data: V1 = VB = 0.1 m3 TA = TB = 20°C = 20 + 273 = 293 K pA = 2.5 MPa = 2500 kPa pB = 1 MPa = 1000 kPa Solution: Problem 5.15 A mixture of gases contains 50% N2, 40% O2 and 10% CO2 by mass. 2 kg of the mixture is compressed from 200 kPa and 293 K to 400 kPa polytropically which follows the pV1.2 = C. Determine the work done, heat transferred and change in entropy. Take (Cp)N2 = 1.04 kJ/kgK, (Cp)o2 = 0.918 kJ/kgK (Cp)co2 = 0.846 kJ/kgK. Given data: xN2 = 50% = 0.5 xO2 = 40% = 0.4 xCO2= 10% = 0.1 mm = 2 kg p1 = 200 kPa T1 = 293 K p2 = 400 kPa pV1.25 = C CpN2 = 1.04 kJ/kgK CpO2 = 0.918 kJ/kgK Cpco2 = 0.846 kJ/kgK Solution: We know that Problem 5.16 A tank of 1 m3 capacity originally contains O2 at a pressure of 5 bar and 350 K. Nitrogen is introduced without change in temperature until the pressure in the tank becomes 12 bar. Determine the mass of each gas in the tank and partial volume of each gas. Given data: Vm = 1 m3 po2 = 5 bar = 500 kPa To2 = 350 K = TN2 = Tm pm = 12 bar = 1200 kPa Solution: Problem 5.17 A mixture of perfect gases at 23°C contains 60% N2, 15% O2 and 25% CH4 by volume. If the partial of CH4 is 60 kPa, determine the (a) partial pressure of N2 and O2, (b) mass proportion of mixture, (c) gas constant for the mixture and (d) volume per mole of mixture. Given data: Tm = 23°C = 23 + 273 = 296 K yN2 = 60% = 0.6 yO2 = 15% = 0.15 yCH4 = 25% = 0.25 pCH4 = 60 kPa Solution: Problem 5.18 A mixture of 5 kg of N2 and 8 kg of O2 at a pressure of 100 kPa and 303 K is compressed reversibly and adiabatically to a pressure of 500 kPa. Determine the (a) initial and final pressure of each component (b) final temperature (c) change in internal energy, enthalpy (d) entropy and (e) work done on the mixture. Take (Cp)N2 = 1.04 kJ/kgK, (Cp)O2 = 0.914 kJ/kgK. Given data: mN2 = 5 kg mo2 = 8 kg p1 = 100 kPa T1 = 303 K p2 = 500 kPa (Cp)N2 = 1.04 kJ/kgK (Cp)o2 = 0.914 kJ/kgK Solution: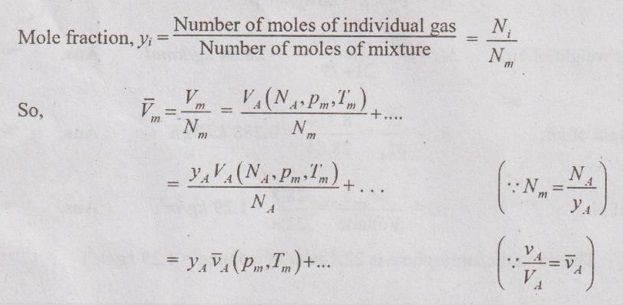
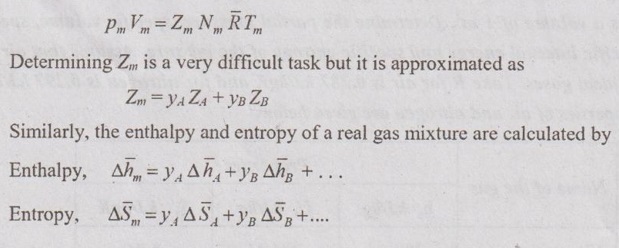
1. Solved Problems on Mixing of Real Gases
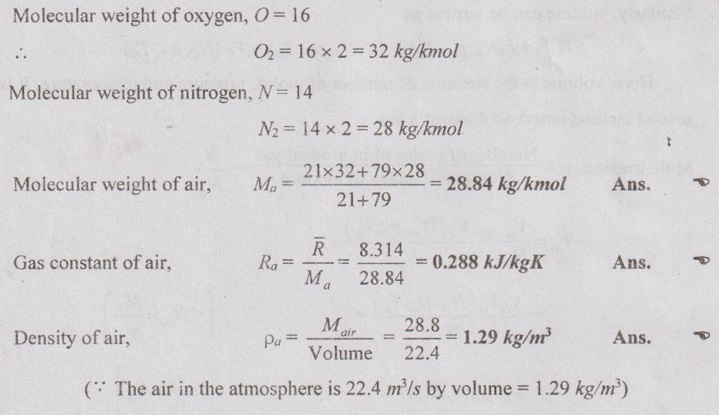


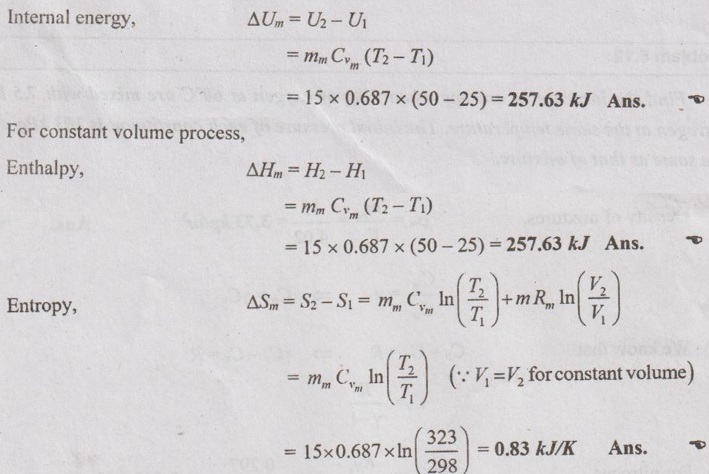


 As per Dalton's law, the final pressure,
As per Dalton's law, the final pressure,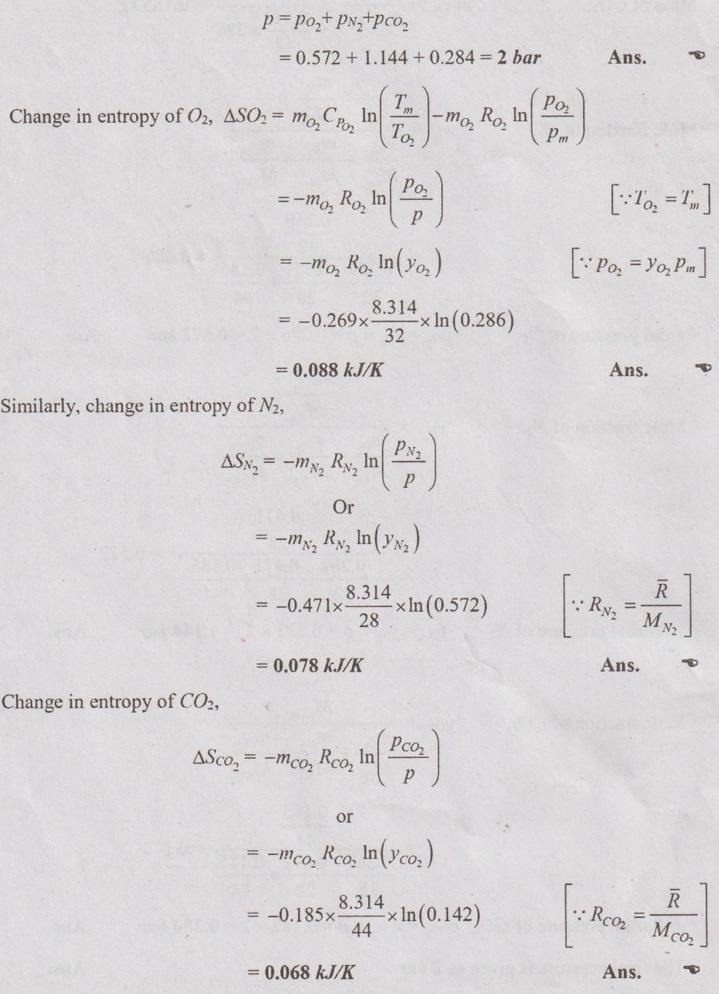

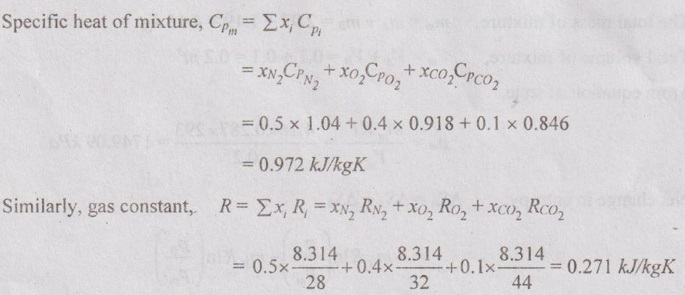

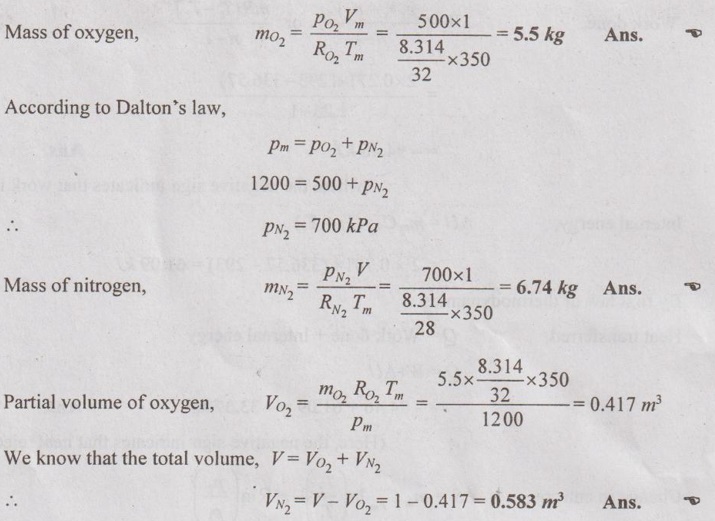


Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : with Solved Example Problems | Thermodynamics - Mixtures of Real Gases
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
