Theory of Machines: Unit II: Gears and Gear Trains
minimum number of teeth to avoid interference
Gears and Gear Trains - Theory of Machines
Now let us derive the relation for minimum number of teeth required on pinion to avoid interference with gear.
MINIMUM NUMBER OF TEETH TO AVOID INTERFERENCE • As explained in Section 4.15.2, in order to avoid interference the path of contact should not extend beyond the interference points M and N. In other words, the addendum circle of pinion or gear must not intersect line of action outside the points of tangency to the two base circles. • For the limiting conditions, we can write Maximum length of path of approach, MP = r sin ϕ and Maximum length of path of recess, PN = R sin ϕ • Since pinion is smaller of the two gears (i.e., r < R), therefore Maximum length of path of approach ≤ Maximum length of path of recess • Since addenda of pinion and gear of standard portions are equal, while increasing addenda is reached first by the addendum circle of gear wheel. Therefore if interference occurs, the interference will occur first between the tip of gear tooth and flank of pinion tooth. • Alternate method: Length of path of contact, KL = KP + PL • To sum up, since limiting condition of interference with standard module is reached first on the flank of pinion teeth, therefore it is necessary to use relation for minimum number of teeth on gear first and then to find out limiting number of teeth on pinion. Now let us derive the relation for minimum number of teeth required on pinion to avoid interference with gear. The maximum value of the addendum radius of gear wheel to avoid interference can be upto O2M, as shown in Fig.4.26. Let ТP = Number of teeth on pinion, TG = Number of teeth on gear wheel, m = Module of the teeth, ϕ = Pressure angle (or angle of obliquity) From triangle O2MP in Fig.4.26, we can write Taking square root on both sides, we get The equation (4.21) gives the limiting or maximum radius of addendum circle of wheel to avoid interference. Let aW = Maximum standard addendum of gear wheel to avoid interference The value of aW is given by aW = AW • m where AW = Addendum coefficient of gear wheel The maximum standard addendum of gear wheel (aW) is also given by In terms of gear ratio G, the above equation can be written as The equation (4.22) gives the minimum number of teeth required on the gear wheel in order to avoid interference. The number of teeth required on pinion in order to avoid interference can be obtained as below. The equation (4.23) gives the minimum number of teeth required on pinion in order to avoid interference. Note 1. Since limiting condition of interference with standard module is reached first on the pinion teeth, therefore first find the minimum number of teeth on gear wheel (using equation (4.22)). and then find the minimum number of teeth on pinion (using the relation TP = TG(min) / G) 2. If the pinion and gear wheel have equal teeth, i.e., G = 1, then equation (4.22) becomes 3. The relation for minimum number of teeth required on pinion to avoid interference in terms of addendum coefficient of pinion (ap) can be derived in similar manner as that for gear wheel (equation (4.23)) and the relation is given by 4. Don't be confused with terms aP & AP, and aW & AW⋅ aP and aW =Addendum of pinion and gear wheel respectively, and AP and AW = Addendum coefficient of pinion and gear wheel respectively. Also aP = AP • m and aW = AW • m Example 4.10 Two gear wheels mesh externally to give a velocity ratio of 3 to 1. The involute teeth has 6 mm module and 20° pressure angle. Addendum is equal to one module. Determine the number of teeth on pinion to avoid interference and the corresponding number on the wheel. Given data: G = TG/TP = 3; m = 6 mm; ϕ = 20°; aP = aW = 1 module Solution: We know that, aW = AW • m (or aP = AP • m) Given that, Mechanics of Machines aW = 1 × module (or aP = 1 × module) ⸫ Addendum coefficient, AW = AP = 1 As discussed already, since limiting condition of interference with standard module is reached first on the flank of pinion teeth, therefore first find TG (min) using equation (4.22) and We know that number of minimum number of teeth on wheel to avoid interference, Now the number of teeth on pinion is given by Example 4.11 In Example 4.10, determine the minimum number on pinion to avoid interference if pinion is meshed with an equal gear wheel. Given data: Refer Example 4.10, ϕ = 20°; m = 6 m; AW = 1. Solution: Given that, TP = TG i.e., G = 1. We know that the number of teeth on gear wheel to avoid interference, when number of teeth on pinion and wheel are equal, Since TW = TP, therefore Number of teeth on pinion to avoid interference, TP = 13 Ans. Example 4.12 Two gear wheels mesh externally and are to give a velocity ratio of 3. The teeth are of involute form of module 6. The standard addendum is 1 module. If the pressure angle is 20° and pinion rotates at 90 rpm, find: (i) the number of teeth on each wheel so that interference is just avoided, (ii) the length of the path of contact, and (iii) the maximum velocity of sliding between the teeth. Given data: Solution: We know that, aW = AW • m Given that, aW = 1 × Module ⸫ Addendum coefficient, AW = AP = 1 (i) Number of teeth on each wheel so that interference is just avoided: We know that minimum number of teeth required on wheel to avoid interference, Now the number of teeth on pinion is given by (ii) Length of path of contact: Pitch circle radii of pinion and gear wheel are given by Addendum circle radii of pinion and gear wheel are given by (iii) Maximum velocity of sliding between the teeth: We know that maximum velocity of sliding between teeth, Example 4.13 A pair of involute spur gears with 20° pressure angle and pitch of module 6 mm is in mesh. The number of teeth in pinion is 16 and its rotational speed is 240 rpm. The gear ratio is 1.75. In order to avoid the interference, determine: (i) addenda on pinion and wheel; (ii) length of path of contact; and (iii) maximum velocity of sliding on either side of pitch point. Given data: ϕ = 20°; m = 6 mm; TP = 16; NP = 240 rpm; G = 1.75 Solution: We know that, Gear ratio, G = TG/TP = 1.75 or Number of teeth on gear wheel, TG = TP × G = 16 × 1.75 = 28 (i) Addenda on pinion and wheel (aP and aW): Addendum on pinion (aP): We know that minimum number of teeth on pinion to avoid interference, Addendum on gear wheel (aW): We know that minimum number of teeth on gear wheel to avoid interference, (ii) Length of path of contact: Pitch circle radii of pinion and gear wheel are given by Addendum radii of pinion and gear wheel are given by (iii) Maximum velocity of sliding on either side of pitch point: Maximum velocity of sliding during approach, Similarly, maximum velocity of sliding during recess, Example 4.14 A pair of spur gears with involute teeth is to give a gear ratio of 3:1. The arc of approach is not to be less than the circular pitch and smaller wheel is the driver, The angle of pressure is 20°. (i) What is the least number of teeth that can be used on each wheel? (ii) What is the addendum of the wheel in terms of circular pitch? Given data: Solution: (i) Least number of teeth on each wheel: Given that the arc of approach is not to be less than the circular pitch. Therefore, (ii) Addendum of the gear wheel in terms of circular pitch: We know that the minimum number of teeth on gear wheel to avoid interference, Example 4.15 Two 20° involute spur gear have a module of 10 mm. The addendum is equal to one module. The larger gear has 40 teeth while the pinion has 20 teeth. Will the gear interfere with the pinion? Given data: ϕ = 20°; m = 10 mm; aP = aW = 1 module = 10 mm; TG = 40; TP = 20 Solution: Pitch circle radii of pinion and gear wheel are given by Addendum circle radii of pinion and gear wheel are given by Length of path of approach is given by To avoid interference, the maximum length of the path of approach is given by MP = r sin ϕ = 100 sin 20° = 34.2 mm We know that the condition to check whether interference occurs or not, Length of path of approach ≤ Maximum length of path of approach i.e., KP ≤ MP i.e., Since KP < MP (i.e., 25.3 mm ≤ 34.2 mm), therefore no interference occurs. Ans. Note The above problem can also be solved by using the following conditions. To check whether interference occurs or not, the alternative conditions are: (i) Length of recess (PL) ≤ Maximum length of path of recess (PN) (ii) Length of path of contact (KL) ≤ Maximum length of path of contact (MN) Example 4.16 Two 20° involute spur gears have a module of 10 mm. The addendum is one module. The larger gear has 50 teeth and the pinion 13 teeth. Does the interference occur? If it occurs, to what value should the pressure angle be changed to eliminate interference. Given data: ϕ = 20°; m = 10 mm; aP = aW = 1 module = 10 mm; TG = 50; TP = 13. Solution: (i) To check whether interference occurs or not: Pitch circle radii of pinion and gear wheel are given by Addendum circle radii of pinion and gear wheel are given by Length of path of approach is given by To avoid interference, the maximum length of path of approach is given by MP = r sin ϕ = 65 sin 20° = 22.23 mm We know that the condition to check whether interference occurs or not, Length of path of path of contact (KP) ≤ Maximum length of path of contact (MP) Since KP > MP (i.e., 25.9 mm > 22.23 mm), therefore interference occurs. Ans. (ii) New value of pressure angle to eliminate interference: Let ϕ = New value of pressure angle to eliminate interference. The interference will not occur, when the length of path of contact atleast is equal to the maximum length of path of contact. i.e.. For no interference, KP = MP Squaring on both sides, we get Thus, if the pressure angle is increased from 20° to 21.88°, the interference can be avoided.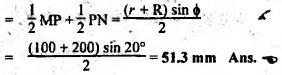
1. Minimum Number of Teeth on Gear Wheel to Avoid Interference

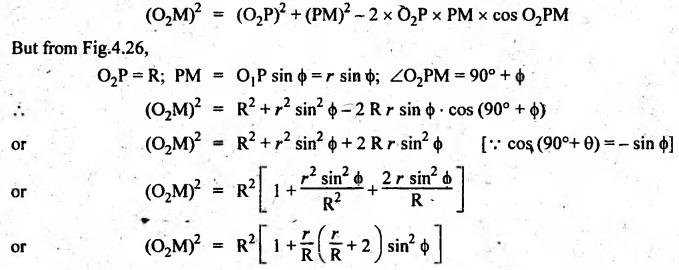
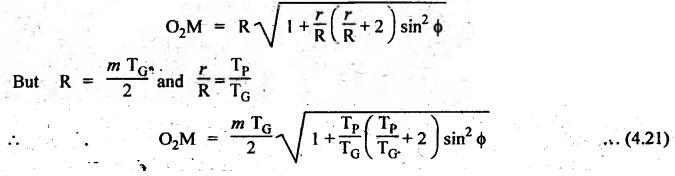

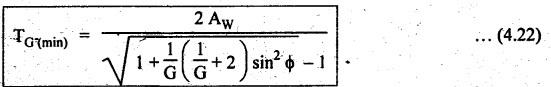
2. Minimum Number of Teeth on Pinion to Avoid Interference



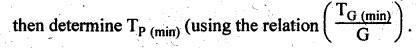

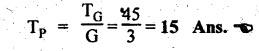
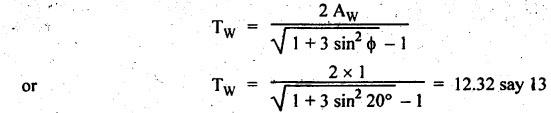
![]()
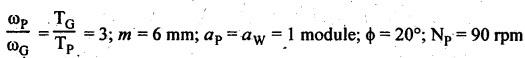
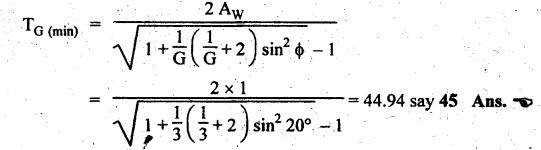

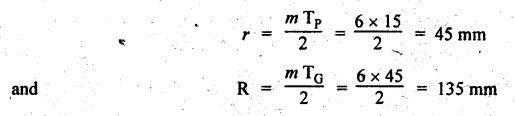

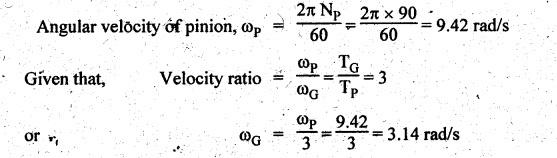
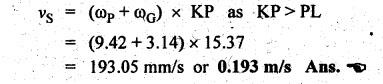
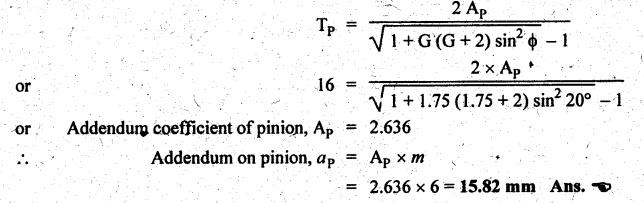
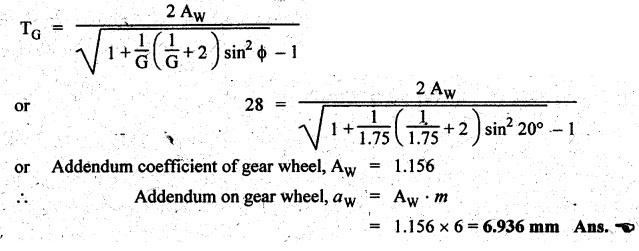
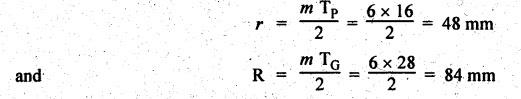

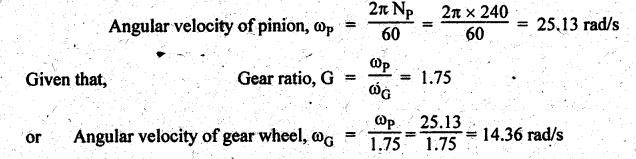

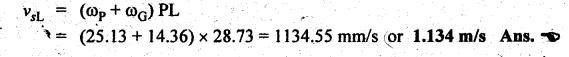
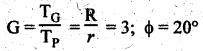

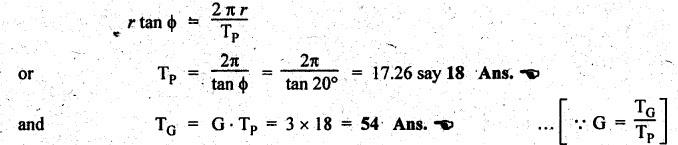

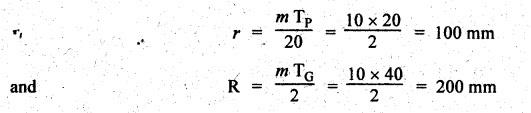
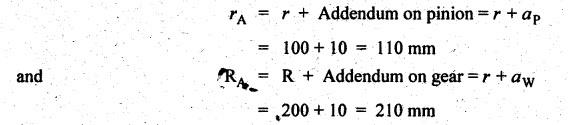
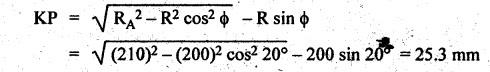
![]()
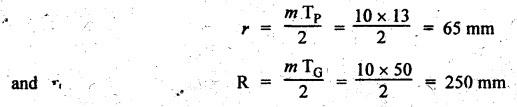


![]()
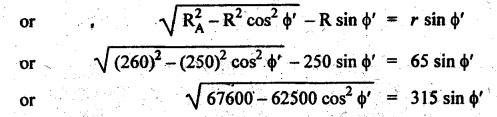
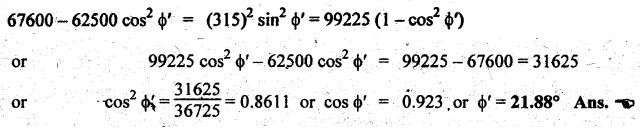
Theory of Machines: Unit II: Gears and Gear Trains : Tag: : Gears and Gear Trains - Theory of Machines - minimum number of teeth to avoid interference
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
