Basic Electrical and Electronics Engineering: Unit IV: Digital Electronics
Minimisation of Boolean Functions
with solved example problems
Boolean algebra and theorems are used for the manipulates of logical expressions.
MINIMISATION OF BOOLEAN FUNCTIONS Boolean algebra and theorems are used for the manipulates of logical expressions. It has also been seen that a logical expression can be realized by using the logic gates. The number of gates required and the number of input terminals for the gates for the implementation of a logical expression, in general, get reduced considerably if the expression can be simplified. Therefore, the simplification of logical expression is very important as it saves the hardware required to design a specific system. We know that logical expressions are implemented by connecting specific logic gates. These logic gates produce a specific output for certain specified combinations of input variables, with no storage involved. These circuits are commonly known as combinational circuits. In combinational circuits, the output level is always dependent on the combinations of the input levels. The combinational circuits can be specified in one of the following ways: ● A set of statements, ● Boolean expression, and ● Truth table To implement a Boolean function with a less number of gates we have to minimize literals and the number of terms. Usually, literals (Boolean variables in complemented or uncomplemented form) and terms are arranged in one of the two standard forms of switching equations : ● Sum of product form (SOP) and ● Product of sum form (POS) The words sum and product are derived from the symbolic representations of the OR and AND functions by + and (addition and multiplication), respectively. But we realize that these are not arithmetic operators in the usual sense. A product term is any group of literals that are ANDed together. For example, ABC, XY and so on. A sum term is any group of literals that are ORed together such as A + B + C, X + Y and so on. A sum of products (SOP) is a group of product terms ORed together. Some examples of this form are: Each of these sum of products expressions consist of two or more product terms (AND) that are ORed together. Each product term consists of one or more literals appearing in either complemented or uncomplemented form. For example, in the sum of products expression ABC + A product of sums is any groups of sum terms ANDed together. Some examples of this form are Each of these product of sums expressions consist of two or more sum terms (OR) that are ANDed together. Each sum term consists of one or more literals appearing in either complemented or uncomplemented form. 3. Canonical Logic Forms We can realize that in the SOP form and in the POS form, all the individual terms to not involved all literals. For example, in expression AB + Let us see one standard sum of products expression : Here, the original expression is standard sum of products, but the simplified expression is not a standard sum of products. It is only sum of products. Similarly, we can say that a product of sums is a canonical (standard) product of sums is every sum terms involves every literal or its complement. For example, Y = (A + B + C) (A + Sum of products form can be converted to standard sum of products by ANDing the terms in the expression with terms formed by ORing the literal and its complement which are not present in that term. For example for a three literal expression with literals A, B and C, if there is a term AB, where C is missing, then we form term (C + Problem 4.31 Convert the given expression in Canonical SOP form: Y = AC + AB + BC Solution: Y = AC + AB + BC Problem 4.32 Convert the given expression in Canonical SOP form: Y = A + AB + ABC Solution: Similarly product of sums form can be converted to standard product of sums by ORing the terms in the expression with terms formed by ANDing the variable and its complement which are not present in that term. For example for a three literal expression with literals A, B and C if there is a term A + B where literal C is missing, then form term C. Problem 4.33 Convert the given expression in Canonical POS form : Y = (A + B) (B + C) (A + C) Solution : Problem 4.34 Convert the given expression in Canonical POS form : Y = A (A + B) (A + B + C) Solution : Each individual term in canonical SOP form is called minterm and each individual term in canonical POS form is called maxterm. The concept of minterms and maxterms allows us to introduce a very convenient shorthand notations to express logical functions. Table 4.7 gives the minterms and maxterms for a three literal/variable logical function where the number of minterms as well as maxterms is 23 = 8. In general, for an n- variable logical function there are 2n minterms and an equal number of maxterms. As shown in table 4.7 each minterm is represented by mi and each maxterm is represented by Mi, where the subscript i is the decimal number equivalent of the natural binary number. With the shorthand notations logical function can be represented follows: where Σ denotes sum of product while π denotes product of sum. We know that logical expression can be represented in the truth table form. It is possible to write logic expression in canonical SOP or POS form corresponding to a given truth table. The logic expression corresponding to a given truth table can be written in a canonical sum of products form by writing one product term for each input combination that produces an output of 1. These product terms are ORed together to create the canonical sum of products. Consider, for example, the following truth table: We can note that Y is 1 when A = 0, B 1 and C = 0, so this particular combination makes the output of an AND gate equal to 1 when The logic expression corresponding to a truth table can also be written in a canonical product of sums form by writing one sum term for each output 0. The sum terms are expressed by writing complement of a variable when it appears as an input 1, and the variable itself when it appears as an input 0. Consider, for example, the following truth table : The sum corresponding to input combinations 010 is A + A product of sums form derived from a truth table is logically equivalent to a sum of products form derived from the same truth table. Let us write the standard SOP and POS from the previous truth table : Now by simplifying equation in the POS form we have, Converting to standard sum of products we have, Therefore, we can say that POS and SOP derived from the same truth table are logically equivalent. In terms of minterms and maxterms we can then write Y = m0 + m1 + m2 + m4 + m6 + m7 = M2 + M5 = Σ m (0, 1, 3, 4, 6, 7) = л M (2, 5) From the above expressions we can easily notice thate there is a complementary type of relationship between a function expressed in terms of maxterms. Using this complementary relationship we can find logical function in terms of maxterms if function in minterms is known or vice-versa. For example, for a four variables if Y = Σ m (0, 2, 4, 6, 8, 10, 12, 14) Then Y = π M (1, 3, 5, 7, 9, 11, 13, 15)1. Introduction
2. Boolean Functions
1. Sum of Product Form
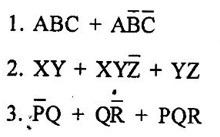
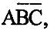 the first product term contains literals A, B and C in their uncomplemented form. The second product term contains B and C in their complemented (inverted) form.
the first product term contains literals A, B and C in their uncomplemented form. The second product term contains B and C in their complemented (inverted) form.2. Product of Sum Form
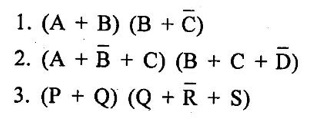
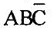 the first product term does not contain literal C. If each term in SOP and POS forms contain all the literals then these are known as canonical (standard) SOP and POS, respectively. For example, in expression
the first product term does not contain literal C. If each term in SOP and POS forms contain all the literals then these are known as canonical (standard) SOP and POS, respectively. For example, in expression 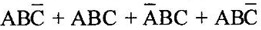 all the literals are present in each product term. In other words we can say that a sum of products is a canonical (standard) sum of products if every product term involves every literal or its complement.
all the literals are present in each product term. In other words we can say that a sum of products is a canonical (standard) sum of products if every product term involves every literal or its complement.
![]() + C)
+ C)4. Converting Expressions in Canonical SOP or POS forms
![]() ) and AND it with AB. Therefore, we get AB (C +
) and AND it with AB. Therefore, we get AB (C + ![]() ) = ABC + AB
) = ABC + AB![]() .
.

![]() and A + B with it. Therefore, we get,
and A + B with it. Therefore, we get,


5. Minterms and Maxterms


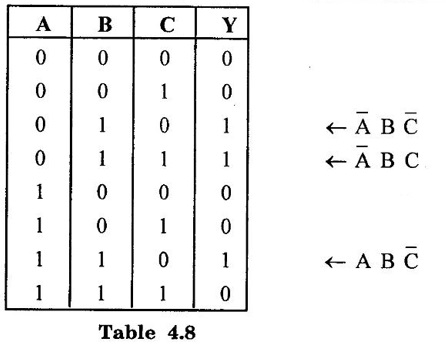
![]() and B and
and B and ![]() are equal to 1. Thus
are equal to 1. Thus 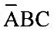 is one product term. Similarly, the other two product terms are
is one product term. Similarly, the other two product terms are 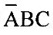 and
and 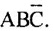 Thus, the canonical sum of products form is
Thus, the canonical sum of products form is
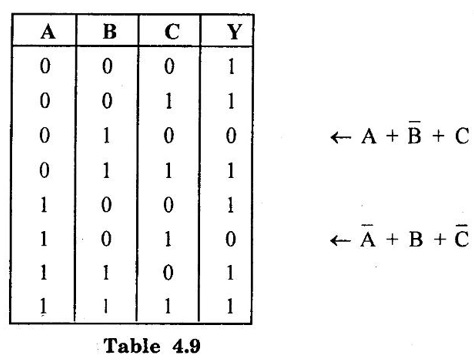
![]() + C, and the sum corresponding to input 101 is
+ C, and the sum corresponding to input 101 is 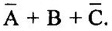 Thus, the standard product of sums form is:
Thus, the standard product of sums form is: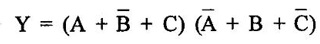



Basic Electrical and Electronics Engineering: Unit IV: Digital Electronics : Tag: : with solved example problems - Minimisation of Boolean Functions
Related Topics
Related Subjects
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation

