Engineering Physics: Unit I: Mechanics
Mechanics: Linear and Rotational motion
Examples with Definition, Formula, Unit
Inertia is the reluctance of the system to change its state of rest or of uniform motion. In case of linear motion mass is the inertia of the system
1. Mechanics Multiparticle dynamics: Center of mass (CM) - CM of continuous bodies - motion of the CM - kinetic energy of system of particles. Rotation of rigid bodies: Rotational kinematics – rotational kinetic energy and moment of inertia – theorems of M.I – moment of inertia of continuous bodies - M.I of a diatomic molecule - torque - rotational dynamics of rigid bodies - conservation of angular momentum - rotational energy state of a rigid diatomic molecule - gyroscope torsional pendulum - double pendulum - Introduction to non-linear oscillations. Introduction • Inertia is the reluctance of the system to change its state of rest or of uniform motion. In case of linear motion mass is the inertia of the system. • But in the case of rotational motion inertia of rigid body plays a very important role in the industrial applications where both rotational and translational operations are to be coupled. • Its principle is also used widely in the design, fabrication and working of several machines of common use namely cranes, motors, lathes, lifting devices, soil testing machines, hydraulic systems, in the design of and fixing the position of huge reactors, etc. • Thus, being the student of technology one should understand the role of moment of inertia in rotational motion as well as the relation between translational and rotational motion of a rigid body. • Many equations of rotational motion could be written by simply replacing the parameters in the equations of linear motion with the appropriate analogous parameters in the rotational motion. Some of the pairs of analogous parameters are given below, followed by their definitions. Definition of Terminology in Linear Motion Displacement: The change of position of a particle in a particular direction is called displacement. If the direction is along x-axis, then the displacement is x. It is measured in metre (m). Velocity (v): The rate of change cf displacement is called velocity. It is given by, S.I unit of velocity is m/s or ms-1 Acceleration S.I unit of acceleration is m/s2 (or) ms-2 Momentum Force (F): The product of mass and acceleration of a particle or a body is called force. It is given by, S.I unit is kgms-2 (or) newton (or) N Definition of terminology in rotational motion Angular displacement (θ): The angle described by a rigid body from its rest position in given time is called angular displacement. Its unit is radian. Angular velocity (ω): The rate of change of angular displacement is called angular velocity. It is given by S.I unit of angular velocity is radian/s Angular acceleration (α): The rate of change of angular velocity is called angular acceleration. It is given by S.I unit of angular acceleration is radian / s2 Angular momentum (L): The moment of momentum is called angular momentum. It is given by It's is unit is kgm2 s-1 Torque (τ): The moment of the applied force about the axis of rotation is called torque. It is given by S.I. unit is Nm (i) Relation between linear velocity and angular velocity (ii) Relation between linear acceleration and angular acceleration ( The linear acceleration is given by
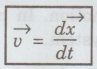
 The rate of change of velocity is called acceleration.
The rate of change of velocity is called acceleration.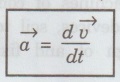
![]() : The product of mass and velocity of the particle or of a body is called momentum. It is given by
: The product of mass and velocity of the particle or of a body is called momentum. It is given by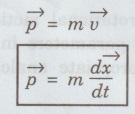
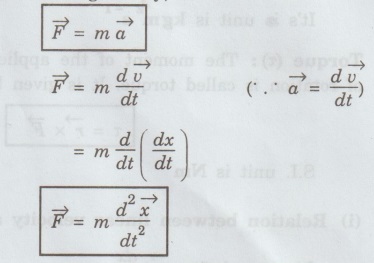
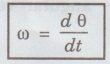
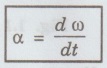
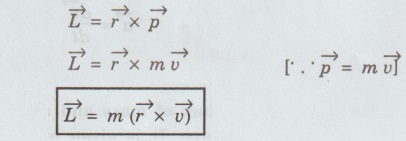
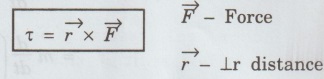

![]() and α)
and α) 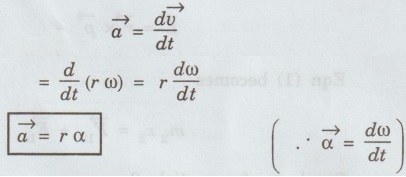
Engineering Physics: Unit I: Mechanics : Tag: : Examples with Definition, Formula, Unit - Mechanics: Linear and Rotational motion
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
