Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Maxwell's Equations
Thermodynamics
Maxwell's equations relate the entropy to the three directly measurable properties such as p, v and T for pure simple compressible substances.
MAXWELL'S EQUATIONS Maxwell's equations relate the entropy to the three directly measurable properties such as p, v and T for pure simple compressible substances. From first law of thermodynamics, Q = W + ΔU Rearranging the parameters, Q = ΔU + W Tds = du + pdv [⸪ Q = Tds and W = pdv] So, du equation becomes, dh = Tds - pdv + vdp + pdv = Tds + vdp …. (5.50) By Helmotz's function, a = u - Ts ⸫ da = du - d(Ts) = du – Tds - sdT ….. (5.51) Substituting the value of du (5.48) in equation (5.51), da = Tds - pdv - Tds - sdT=-pdv – sdT ... (5.52) By Gibbs functions G = h - Ts Dg = dh - d(Ts) = dh - Tds – sdT ... (5.53) Substituting the value of dh (5.50) in equation (5.53), So, dg becomes dg= Tds + vdp – Tds – sdT (⸪ dh = Tds + vdp) dg = vdp – sdT ... (5.54) By inverse exact differential, it can be written the equation (5.48) as du = Tds – pdv ... (5.55) These equations (5.58), (5.59), (5.60) and (5.61) are Maxwell's equation.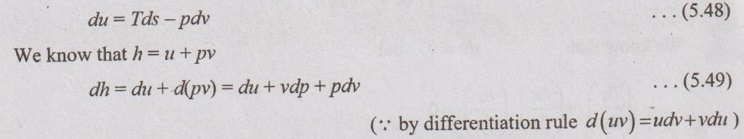 Substituting the value du in equation (5.49),
Substituting the value du in equation (5.49), Similarly, the equation (5.54) can be written as
Similarly, the equation (5.54) can be written as
Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : Thermodynamics - Maxwell's Equations
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
