Matrices and Calculus: Unit II: Differential Calculus
Maxima and Minima of a Function of one variable
Definition, Theorem, Geometrical Meaning, Tests, Worked Examples, Exercise with Answers | Differential Calculus
We have already seen the applications of derivative in problems of tangent and normal, in deciding increasing and decreasing nature of a function in an interval.
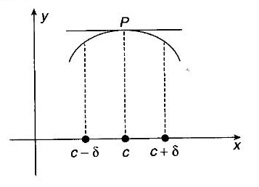
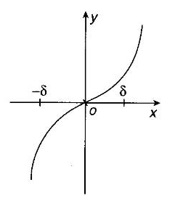
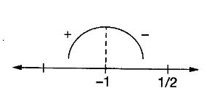
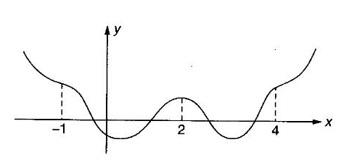
MAXIMA AND MINIMA OF A FUNCTION OF ONE VARIABLE We have already seen the applications of derivative in problems of tangent and normal, in deciding increasing and decreasing nature of a function in an interval. We shall now use it to locate maxima and minima of a function. In calculus the term "maximum" is used in two senses “absolute” maximum and "relative" maximum. Similarly, absolute minimum and relative minimum. Definition 2.21 Let f be the function defined on [a, b] and let c ∈ (a, b). Then (i) f is said to have a relative maximum (or local maximum) at c, if there is a neighbourhood (c - δ, c + δ) of c such that f(x) < f(c) ∀x ∈ (c - δ, c + δ), x ≠ c. That is f(c) is the greatest value in a neighbourhood of c. (ii) f is said to have a relative minimum (or local minimum) at c, if there is a neighbourhood (c - δ, c + δ) of c suchthat f(x) > f(c) ∀x ∈ (c - δ, c + δ), x ≠ c. That is f(c) is the least value in a neighbourhood of c. Note (1) If f(c) is a relative maximum or relative minimum, then f(c) is called an extreme value of ƒ at c or extremum of f at c. Definition 2.22 Let f be defined on [a, b]. f is said to have an absolute maximum (or global maximum) on [a, b] if there is at least one point c ∈ [a, b] such that f(x) ≤ ƒ(c) ∀x ∈ [a, b]. In otherwords, the largest value of ƒ on [a, b] is called the absolute maximum Definition 2.23 Let f be defined on [a, b]. f is said to have an absolute minimum (or global minimum) on [a, b] if there is at least one point c ∈ [a, b] such that f(x) ≥ ƒ(c) ∀x ∈ [a, b]. That is the least value of ƒ on [a, b] is called the absolute minimum (or global minimum). Note 1. Given a function f defined on [a, b], the absolute maximum and the absolute minimum need not exist. Then ƒ has no absolute maximum on [0, 1]. However, if f is continuous on a closed and bounded interval [a, b], then absolute maximum and absolute minimum exist at some points c, d in [a, b]. 2. From the definition of maximum and minimum it is obvious that ƒ(c) is an extreme value of ƒ at c, iff f(x) – f(c) keeps the same sign for all x, other than c, in some neighbourhood of c. Theorem 2.11 A necessary condition for the existence of an extremum at an interior point Let f be a function defined on the interval [a, b] and c ∈ (a, b). If f(c) is an extremum at c and if f'(c) exists, then f'(c) = 0. This theorem is known as Fermat's theorem. Let y = f(x) be the graph of ƒ on [a, b], then P(c, f(c)) is a point on the curve y = ƒ(x). If f(c) is a maximum value, then in (c - δ, c] the curve is increasing and so f'(x) > 0 in (c - δ, c) and decreasing in (c, c + δ). That is f'(x) < 0 in (c, c + δ). If f'(c) exists, then f'(c) must be zero. That is the tangent is parallel to the x-axis, because it is increasing up to the point P and momentarily at rest at P and then decreasing. Similarly, if f(c) is a minimum value, then f'(c) = 0. Note 1. The points where f'(x) = 0 are called stationary points of f. 2. The converse of the above theorem is not true. Similarly, if f'(c) = 0, then f(c) is not an extremum. For example: Consider f(x) = x3. f'(x) = 3x2 ⸫ ƒ'(0) = 0. But f(0) is neither a maximum nor a minimum because there is no neighbourhood of 0 in which ƒ(x) – ƒ(0) keeps the same sign for x ≠ 0. 3. It is possible that f(c) is an extreme value of f even if f'(c) does not exist. For example: Consider We know that f'(0) does not exist. But f(0) is a minimum value of ƒ(x). In fact, ƒ(0) is the absolute minimum. Definition 2.24 Critical Points Let f be a function defined on [a, b]. The points x ∈ (a, b) at which f' (x)=0 or f'(x) does not exist are called critical points of f. For f(x) = |x|, x = 0 is a critical point but not a stationary point. (1) Second Derivative Test Let f be a function defined on [a, b] and let ƒ be twice differentiable in a neighbourhood (c − δ, c + δ) of c ∈ (a, b) and f'(c) = 0. Suppose ƒ"(c) ≠ 0, then 1. f(c) is a maximum if ƒ"(c) < 0 and 2. f(c) is a minimum if ƒ"(c) > 0. Note If ƒ"(c) = 0, then the second derivative test cannot be applied. In this case, we use the following general test involving higher derivatives or the first derivative test. (2) General Test Let f be differentiable n times and f'(c) = 0, ƒ"(c) = 0,..., f(n-1) (c) = 0 and f(n)((c) ≠ 0. If n is even, then 1. f(c) is a maximum if f" (c) < 0 2. f(c) is a minimum if f"(c) > 0. If n is odd, then f(c) is neither a maximum nor a minimum. (3) First Derivative Test Let f be defined on [a,b] and c ∈ (a,b). Let f be differentiable in a neighbourhood (c - δ, c + δ) of c, except possibly at c. (i) If f'(x) > 0 for x < c and f'(x) < 0 for x > c in the neighbourhood of c, then f(c) is a maximum value. That is, f'(x) changes from positive to negative in the neighbourhood of c as x increases. (ii) If f'(x) < 0 for x < c and f'(x) > 0 for x > c in the neighbourhood of c, then f(c) is a minimum value. That is, f'(x) changes from negative to positive in the neighbourhood of c as x increases. Example 1 Find the absolute maximum and minimum of the function Solution Given Since f(x) is a polynomial, it is continuous and differentiable in the closed interval (-1/2, 4). So absolute maximum and minimum will occur at a critical point or at the end points. Differentiate (1) w. r to x we get f'(x) = 3x2 - 6x, Since there is no point where f is not differentiable, all the critical points are given by f'(x) = 0 The largest value is 17 and so it is the absolute maximum and it occurs at the end point x = 4. The smallest value is -3 and so it is the absolute minimum and it occurs at the critical point x = 2 Example 2 Find the absolute maximum and minimum of Solution Since the internal (1, 3) is open, absolute maximum or absolute minimum can occur only at the critical points. So, f has an absolute minimum at x = 4/3 There is no absolute maximum Example 3 Find the local maximum and minimum of the function f(x) = x + 2 sin x, 0 ≤ x ≤ 2π. Solution Given f(x) = x + 2 sin x, 0 ≤ x ≤ 2π Example 4 Investigate the maximum and minimum values of the function Solution Given ⸫ the only critical points x = -1, 1 II Derivative Test We have ⸫ y is minimum when x = -1 Example 5 f(x) is a cubic polynomial attaining the maximum and minimum values 10 and -5/2 at x = -3 and x = 2 respectively. Find f(x). Solution Given f(x) is a cubic polynomial ⸫ f'(x) is a quadratic Given at x = -3, x = 2 maximum and minimum occurs ⸫ they are roots of the quadratic ƒ'(x) = 0 ƒ'(x) = a(x + 3) (x − 2) = a(x2 + x - 6) We want to find f(x) and so integrate f'(x) Example 6 Find the maxima and minima of the function 10x6 - 24x5 +15x4 − 40x3 + 108. Solution. Let ƒ(x) = 10x6 - 24x5 +15x4 − 40x3 + 108. Example 7 Find the maxima and minima of the function x5 - 5x4 + 5x3 + 10 Solution Example 8 Find the area of the largest rectangle with lower base on x-axis and upper vertices on the curve y = 12 - x2 Solution Given curve is y = 12 – x2 Since the curve is symmetric about y-axis, the rectangle must be symmetrical about the y-axis Let S be the area of the rectangle. Example 9 Find two positive numbers such that their sum is 4 and the sum of the square of one and the cube of the other is a maximum Solution Let x and y be numbers such that x + y = 4 ⇒ y = 4 - x But 6 ∉ (0, 4) Example 10 What is the maximum slope of the curve y = -x3 + 3x2 + 9x - 27 and at what points is it? Solution The given curve is y = -x3 + 3x2 + 9x - 27. (1) The slope of a curve at a point on it is the same as the slope of the tangent at that point. Differentiating with respect to x, we get We have to maximize m. ⸫ when x = 1, m is maximum. Then y = -1 + 3⸱1 + 9⸱1 – 27 = -16 ⸫ the point at which maximum slope occurs is (1, −16) and the maximum slope = 12. Example 11 Find the maximum and minimum values of f(x) = |4 - x2|, x ∈ [−4, 4]. Also find the absolute maximum and absolute minimum, if they exist. Solution Let f(x) = |4 - x2|, x ∈ [−4, 4] We know At x = -2, 2, f'(x) does not exist. [Since, ƒ is continuous at x = 2 and ƒ'(2−) = −4, ƒ'(2+) = 4 ⸫ f'(2) does not exist. Similarly, f' (-2), does not exist] The critical points are x = 0, - 2, 2. When x = 0, ƒ"(0) = −2 < 0. ⸫ f(x) has a maximum at x = 0 and the maximum value = 4. Since f'(x) does not exist at x = -2, x = 2, we use the first derivative test. In a neighbourhood of -2, f'(x) < 0 if x < -2 and f'(x) > 0 if x > -2. i.e., f'(x) changes from -ve to +ve as x increases in the ngd. of -2 So, f(-2) is a minimum and the minimum value = 4. Similarly, in a neighbourhood of 2, f'(x) < 0 if x < 2 and f'(x) > 0 if x > 2. So, ƒ(2) is a minimum and the minimum value is zero. The least value of f(x) in [−4, 4] is 0. ⸫ the absolute minimum = 0. Though ƒ(0) = 4 is a relative maximum, it is not the absolute maximum. Absolute maximum occur at the end points x = 4 or x = -4 and the value is ƒ(4) = |4 - 42| = |4 - 16| = |-12| = 12. Example 12 In a submarine cable the speed of signalling varies as Solution Let S be the speed of signalling in a submarine cable. Then Example 13 Find the local maximum and minimum values of Solution Example 14 Find the local maxima and minima of the function f(x) = 4x3 + 3x2 - 6x + 10 using first derivative test. Solution Given f(x) = 4x3 + 3x2 - 6x + 10 f'(x) = 12x2 + 6x - 10 = 6(2x2 + x - 1) = 6(2x - 1) (x + 1) The critical points are given by f'(x) = 0 ⇒ 6(2x − 1) (x + 1) = 0 ⇒ x = 1/2 or - 1 Now we find maximum or minimum using first derivative test we study the change of sign of derivative in a neighborhood, of critical points. In a neighborhood of x = -1, f'(x) changes from positive to negative and so, at x = -1, f(x) has a local maximum The maximum value is ƒ(−1) = 4 (−1)3 + 3(−1)2 − 6(−1) + 10 = 4 + 3 + 6 + 10 = 15 In a neighborhood of x = 1/2, Example 15 Find the local maxima and minima of the function f(x) = 2x3 + 3x2 - 36x + 5, using (i) first derivative test (ii) Second derivative test Solution Given f(x) = 2x3 + 3x2 - 36x + 5 ƒ'(x) = 6x2 + 6x – 36 (1) = 6(x2 + x − 6) = 6(x + 3) (x − 2) The critical points are given by f'(x) = 0 ⇒ 6(x + 3)(x - 2) = 0 (i) By First derivative test we have f'(x) = 6(x + 3)(x - 2) We study change of derivative f'(x), in a neighborhood of the critical points. ⸫ f'(x) changes from positive to negative and so at x = -3, f(x) has a local maximum The maximum value is f(−3) = 2 (−3)+ + 3(−3)2 − 36(−3) + 5 = 86 In a neighborhood of 2, ⸫ f'(x) changes from negative to positive and so at x = 2, f(x) has a local minimum The minimum value is f(2) = 2⸱23 +3⸱22 - 36·2 + 5 = -39 (ii) By second derivative test we have by (1), ƒ'(x) = 6x2 + 6x – 36 ⸫ ƒ"(x) = 12x + 6 when x = -3, f" (-3)= 12(-3) + 6 = −30 < 0 ⸫ f(x) is a maximum at x = -3 and maximum value is f(-3) = 86 when x = 2, ƒ"(2) = 12(3) + 6 = 42 > 0 ⸫ f(x) is a minimum at x = 2 and the minimum value is f(2) = −39 Example 16 Find the local maxima and minima of the function f(x) = x2 – x -In x, x > 0, by using the first derivative test. Solution Given f(x) = x2 – x - ln x; x > 0 is the domain To find critical points, solve ƒ'(x) = 0 ⸫ f'(x) changes from negative to positive and so at x = 1, f(x) has a minimum The minimum value is f(1) = 12 - 1 – ln l = 0 Example 17 Suppose the derivative of a function ƒ is ƒ'(x) = (x + 1)2 (x − 2)3 (x − 4)4, find (i) the intervals in which f is increasing or decreasing. and (ii) the points where f(x) is a maximum or minimum Solution Given ƒ'(x) = (x + 1)2 (x − 2)3 (x − 4)4 To find critical points, solve f'(x) = 0 ⇒ (x + 1)2 (x − 2)3 (x − 4)4 = 0 ⇒ x = -1, 2 or 4 The critical points divided the domain of the function, (-∞, ∞) into subintervals (-∞, -1), (1, 2), (2, 4), (4, ∞) where the function is either increasing or decreasing. Note We know maxima or minima occurs only at the critical points. But it is not necessary that at a critical point maximum or minimum should occur. In example 17 above we find at the critical points x = -1, x = 4, there is no maximum or minimum. The situation can be visualized from the diagram given below. 1. Find the maximum and minimum values of x5 -5x + 5x3 −1. 2. Find maxima and minima of 2x3 - 3x2 - 36x + 10. 3. Find the maximum and minimum values of a2 sin2 x + b2 cos2x 4. If xy = 4, find the maximum and minimum values of 4x + 9y. 5. Find the maximum and minimum values of | x - x2 | on [2,2]. 6. Show that maximum value of 7. A cubic function f(x) has turning points x = 1, x = -3/2. It vanishes when x = 0, and its value is 4 when x = 2, find the function 8. Find maxima and minima of 9. Find maxima and minima of the function 10. f(x) = a/x + bx has an extremum at x = 2 and f(2) = 1. Determine the values of a and b. Is the point (2, 1) a point of maximum or minimum? 11. Find the maximum possible slope for a tangent line to the curve 12. If 2x + y = 5 find the maximum value of x2 + 3xy + y2. 13. Divide 64 into two numbers such that the sum of their cubes is a minimum 14. Show that the area of a rectangle of given perimeter 20 m is maximum when it is a square? ANSWERS TO EXERCISE 2.11 1. Maximum at x = 2, maximum value = -9 Minimum at x = 3, minimum value = -28 x = 0, is neither maximum or minimum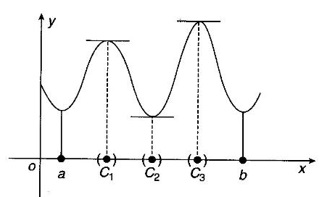
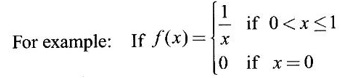
1. Geometrical Meaning
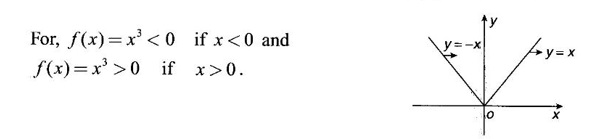
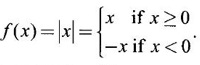
2. Tests for Maxima and Minima
WORKED EXAMPLES
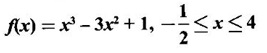
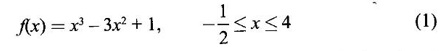
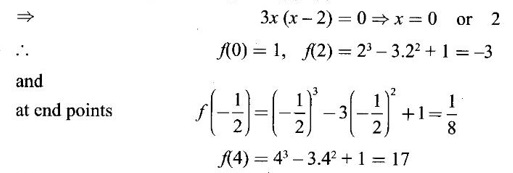
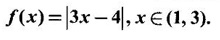


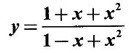

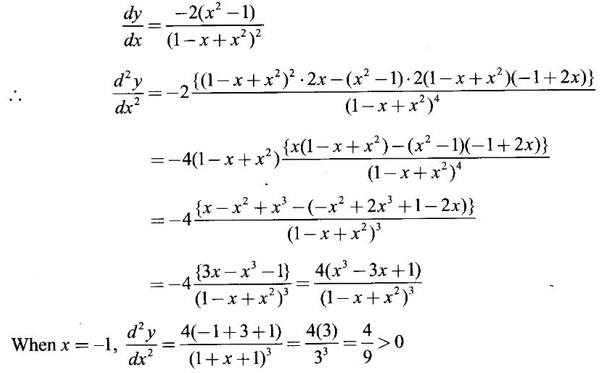
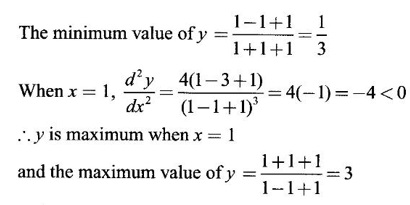







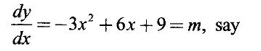
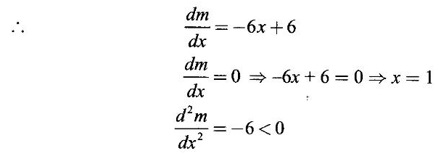

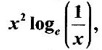 where x is the ratio of the radius of the core to that of the covering. Find the values of x for which the speed of signaling is maximum.
where x is the ratio of the radius of the core to that of the covering. Find the values of x for which the speed of signaling is maximum.
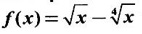 using both first and second derivative tests
using both first and second derivative tests
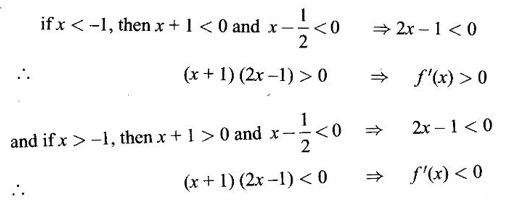
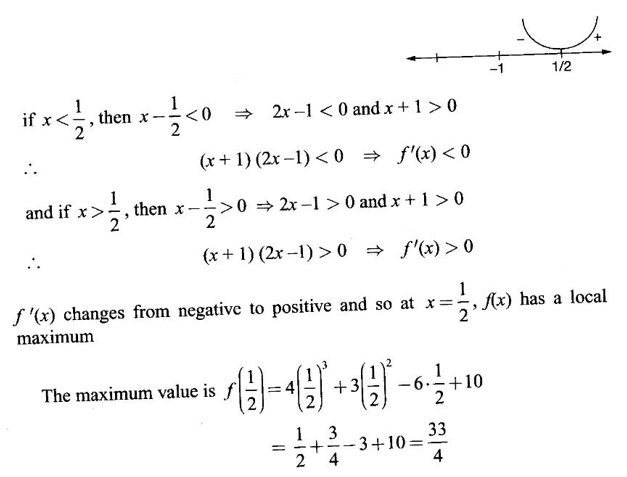
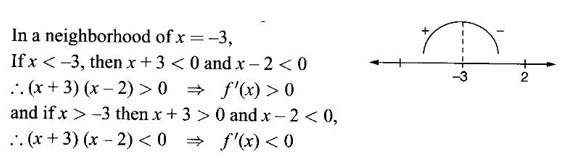
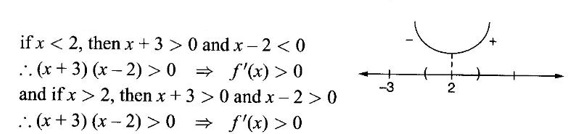
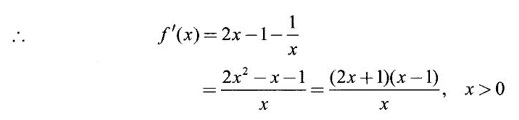


EXERCISE 2.11
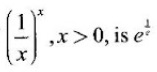
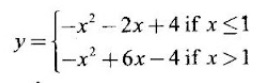
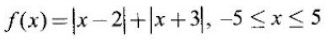
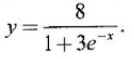

Matrices and Calculus: Unit II: Differential Calculus : Tag: : Definition, Theorem, Geometrical Meaning, Tests, Worked Examples, Exercise with Answers | Differential Calculus - Maxima and Minima of a Function of one variable
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
