Matrices and Calculus: Unit I: Matrices
Matrices: Vector
Worked Solved Examples
The concept of matrices and their basic operations were introduced by the British mathematician Arthur Cayley in the year 1858.
Matrices The concept of matrices and their basic operations were introduced by the British mathematician Arthur Cayley in the year 1858. He wondered whether this part of mathematics will ever be used. However, after 67 years, in 1925, the German physicist Heisenberg used the algebra of matrices in his revolutionary theory of quantum mechanics. Over the years, matrices have been found as an elegant and powerful tool in almost all branches of Science and Engineering like electrical networks, graph theory, optimisation techniques, system of differential equations, stochastic processes, computer graphics, etc. Because of the digital computers, usage of matrix methods have become greatly fruitful. Here we study certain numbers associated with a square matrix, called eigen values and certain vectors associated with them, called eigen vectors. These are useful in the study of canonical forms of a matrix such as diagonalisation and in the study of quadratic forms. The problem of determining eigen values and eigen vectors of a square matrix is called an eigen value problem. We shall now introduce some basic concepts. The vector Definition 1.1.1 An ordered n-tuple (x1, x2, ...,xn) of numbers x1, x2, ...,xn is called an n-dimensional vector. For example the triplet (2, 3,-4) is a 3-dimensional vector. (1, 0, −2, 3) is a 4-dimensional vector. A row matrix is also called a row vector and a column matrix is called a column vector. Definition 1.1.2 If X1 (a1, a2,... an), X2 = (b1, b2, ,... bn) be two n-dimensional vectors, then their sum and scalar multiplications are Definition 1.1.3 Linear combination If X1, X2,… Xr are r vectors of n-dimension and if α1, α2, ..., αr are numbers, then α1X1 + α2X2 + …. + αrXr is called a linear combination of the vectors X1, X2,… Xr. Definition 1.1.4 Linearly dependent and independent vectors (a) The set of vectors X1, X2,… Xr is said to be linearly dependent if there exist numbers α1, α2, ..., αr, not all zero, such that α1X1 + α2X2 + …. + αrXr = 0 (b) The set of vectors X1, X2,… Xr is said to be linearly independent if any relation of the form α1X1 + α2X2 + …. + αrXr = 0 ⇒ α1 = 0, α2 = 0, ..., αr = 0 Note (i) If X1, X2,… Xr are linearly dependent, then some vector is a linear combination of others. (ii) In a plane or 2-dimensional space, non-collinear vectors are linearly independent vectors whereas collinear vectors are dependent vectors. In 3-dimesional space, non-coplanar vectors are linearly independent vectors whereas coplanar vectors are dependent vectors. e.g., (iii) Any set of vectors containing zero vector 0 is a linearly dependent set. (iv) Rank of an m × n matrix A is equal to the maximum number of independent column vectors or row vectors of A. (v) A useful result to test linear independence: Let X1, X2,… Xn be n vectors of n-dimensional space. Let A be the matrix having these n-vectors as columns (or rows). Then A is a square matrix of order n. Example 1 Show that the vectors (1, 2, 3), (3, −2, 1), (1, −6, −5) are linearly dependent. Solution = 1 · (10+6)-3(-10+18)+1·(2+6) = 16 – 24 + 8 = 0 ⸫ the vectors (1, 2, 3), (3, -2, 1) and (1, -6, -5) are linearly dependent. Example 2 Show that the vectors X1 = (1, 2, 3, 4), X2 = (3, 1, 2, 1), X3 =(1, −5, 8, −7) are linearly dependent and find the relation between them. Solution We shall use elementary row operations. Since the maximum number of non-zero rows is 2, which is less than the number of vectors, the given vectors are linearly dependent. The relation between them is obtained as below. Since the rows are vectors, we get X3 - X2 + 2X1 = 0 which is the relation between the vectors. Note The rows of the matrix are the given vectors. So, only row operations must be used to find the relationship between the vectors.INTRODUCTION
1. VECTOR
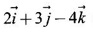 can be regarded as the triplet (2, 3, -4).
can be regarded as the triplet (2, 3, -4).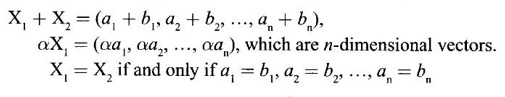
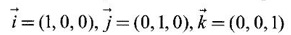 are linearly independent vectors.
are linearly independent vectors.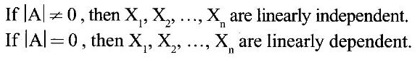
WORKED EXAMPLES
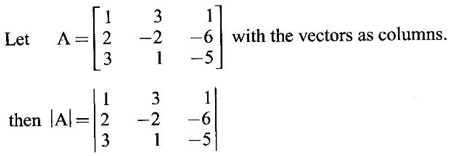
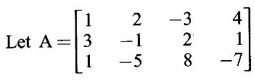 with the vectors as rows.
with the vectors as rows.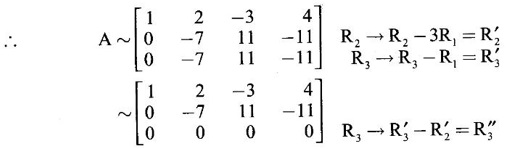
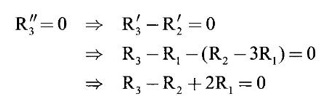
Matrices and Calculus: Unit I: Matrices : Tag: : Worked Solved Examples - Matrices: Vector
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
