Transforms and Partial Differential Equations: Unit I: Partial Differential Equations
Linear partial differential equations of second and higher order with constant coefficients of both homogeneous and non-homogeneous types
Solved Example Problems
Linear partial differential equations of higher order with constant co-efficients may be divided into two categories as given below.
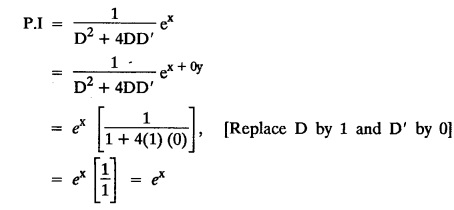
LINEAR PARTIAL DIFFERENTIAL EQUATIONS OF SECOND AND HIGHER ORDER WITH CONSTANT COEFFICIENTS OF BOTH HOMOGENEOUS AND NON-HOMOGENEOUS TYPES Linear partial differential equations of higher order with constant co-efficients may be divided into two categories as given below. (i) homogeneous p.d.e. with constant co-efficients. (ii) non-homogeneous p.d.e. with constant co-efficients. Definition : A linear p.d.e. with constant co-efficients in which all the partial derivatives are of the same order is called homogeneous; otherwise it is called non-homogeneous. A homogeneous linear partial differential equation of nth order with constant co-efficients is of the form equation (i) can be written as Method of finding C.F. 1. To get the auxiliary equation of f(D, D') = F(x, y) put D = m and D' = 1. 2. The auxiliary equation is f(D,D') = 0 i.e., f(m, 1) = 0 To find the complementary functions: Note: To find : Problems based on Homogeneous equations Example 1.5.1: Solve (D2 – 4DD' + 3D'2) z = 0. Solution: Given [D2 - 4DD' + 3D'2] z = 0 The auxiliary equation is m2 - 4m +3 = 0 [Replace D by m and D' by 1] Solving, m2 - 3m - m + 3 m (m - 3) - 1 (m − 3) = 0 (m − 1) (m − 3) = 0 m = 1, m = 3 Here, the roots are distinct Since, R.H.S. is zero, there is no particular integral Hence, the general solution is z = C.F. Example 1.5.2: Solve [D2 - 2DD' + D'2] z = 0. Solution : [D2 - 2DD' + D'2]z = 0. The auxiliary equation is m2 − 2m + 1 = 0 [Replace D by m and D' by 1] i.e., (m − 1)2 = 0 m = 1, 1 Here, the roots are equal Since R.H.S. is zero, there is no particular integral Hence, the general solution is z = C.F Example 1.5.3: Solve [D3 + DD′2 – D2 D′ – D'3] z = 0 Solution: Given [D3 + DD'2 – D2 D' - D'3]z = 0 The auxiliary equation is m3 - m2 + m −1 = 0 [Replace D by m and D' by 1] Here, the roots are distinct Since R.H.S. is zero, there is no particular integral Hence, the general solution is Example 1.5.4: Solve 2r+ 5s - 3t = 0. Solution: The given differential equation can be written as The auxiliary equation is 2m2 + 5m - 3 = 0 [Replace D by m and D' by 1] 2m2 + 6m - m −3 = 0 2m (m + 3) - 1 (m + 3) = 0 (m + 3) (2m − 1) = 0 Here the roots are distinct. Since R.H.S. is zero, there is no particular integral Hence, the general solution is Example 1.5.5 : Solve (D4 – D'4) z = 0 Solution: Here, the roots are distinct Since R.H.S. is zero, there is no particular integral ⸫ Hence, the general solution is I. Solve : [R.H.S = 0, unequal roots] II. Solve [R.H.S = 0, unequal roots of Higher order]. III. Solve : [R.H.S = 0, equal roots] IV. Solve : [R.H.S= 0, different types of roots] Note: To solve [DD' – D'2]z = 0 R.H.S eax+by Replace D by a and D' by b Example 1.5.6 : Solve : Solution: Example 1.5.7: Find the P.I of [D2 + 4DD'] z = ex. Solution: Example 1.5.8 : Solve Solution: Example 1.5.9: Solve (D + D')2 z = ex-y Solution: Given: (D+D')2z = ex-y The auxiliary equation is Example 1.5.10: Find the P.I of (D2 + DD') z = ex-y Solution: Example 1.5.11: Solve (D3 – 3DD'2 + 2D'3) z = e2x − y + ex+y Solution: Hence, the general solution is Find the P.I of the following : R.H.S = x2 y2 Example 1.5.12: Solve [D2 - 7DD' + 6D'2] z = xy Solution : Given: [D2 - 7 DD' + 6D'2]z = xy The auxiliary equation is Example 1.5.13 : Solve [D2 + 3 DD' + 2D'2] z = x + y Solution: Given: [D2 + 3 DD' + 2D'2] z = x + y The auxiliary equation is Example 1.5.14: Solve [D2 + 4DD' - 5D'2] z = x + y2 + π Solution: Given: [D2 + 4DD' - 5D'2]z = x + у2 + π The auxiliary equation is Find the Particular Integral of R.H.S = eax+by + xrys Example 1.5.15 : Solve: [D2 - DD' – 6D'2] z = x2y + e3x + y. Solution: Example 1.5.16: Solve (D2 + DD' - 6D'2) z = x2y + e3x+y. Solution : Example 1.5.17 : Solve (D2 – 6DD' + 5D'2 ) z = ex sinh y + xy Solution: Example 1.5.18: Solve (D2 + 2DD' + D'2) z = x2y + ex-y Solution : EXERCISES Find the Particular Integral of the following : R.H.S = sin (ax + by) or cos (ax + by) Replace D2 by - a2, DD' by - ab, D'2 by - b2 Formulae Example 1.5.19 : Solve [D2 - 2DD' + 2D'2] z = sin (x − y). Solution: Example 1.5.20: Solve [D3 - 4D2D' + 4DD'2] z = 6 sin (3x + 6y). Solution : Given: [D3 - 4D2 D' + 4DD'2] z = 6 sin (3x + 6y) The auxiliary equation is m3 - 4m2 + 4i = 0 Example 1.5.21 : Solve [D2 – 2DD' + D'2] z = cos (x − 3y). Solution: Given: [D2 − 2DD' + D'2]z = cos (x - 3y) Example 1.5 22 : Solve Solution: Example 1.5.23: Solve [D2 – 3DD' + 2D'2] z = sin x cos y Solution : Given: [D2 - 3DD' + 2D'2] z = sin x cos y The auxiliary equation is m2 - 3m + 2 = 0 m = 1, 2 Example 1.5.24: Solve (D2 - DD') z = sin x sin 2y Solution: Given: (D2 - DD')z = sinx sin 2y The auxiliary equation is m2 - m = 0 Find the P.I of the following: R.H.S= sin (ax + by) + eax+by Example 1.5.25: Solve (D3 - 7DD'2 – 6D'3) z = sin(x+2y) + e3x+y. Solution: Example 1.5.26 : Solve : Sol. EXERCISES Find the P.I. of the following: R.H.S = xr ys + sin (ax + by) or cos (ax + by) Example 1.5.27: Solve (D2 + 3DD' – 4 (D')2) z = x + sin y Solution: Example 1.5.28: Solve the equation [D3 – 7 DD'2 – 6 D'3] z = cos (x + 2y) + x Solution: R.H.S = eax+by ϕ(x, y) Replace D by D+a, D' by D'+b Example 1.5.29 : Solve [D2 − 2DD' + D'2] z = x2 y2 ex + y. Solution : Example 1.5.30 : Solve (D3 + D2 D' - DD'2 – D'3) z = excos 2y. Solution: The general solution is z = C.F + P.I R.H.S. = sin ax sin by (or) cos ax cos by Example 1.5.31: Solve [D2 - D'2] z = sin 2x sin 3y Solution: R.H.S = y cos.x (or) y sin x Example 1.5.32 : Solve [D2 + DD' - 6D'2] z = y cos x. (or) (r+ s − 6t) = y cos x Solution: Aliter: To find P.I 3. Non-homogeneous linear equation The linear differential equations which are not homogeneous, are called Non-homogeneous linear equations. Complementary function : Let the non-homogeneous equation be (D – mD' — a) z = 0 Similarly, the solution of (D - mD' - a)2 z = 0 is Working rule Problems based on Non-homogeneous linear equation Example 1.5.34: Solve (D + D' - 2) z = 0 Solution : Given : (D + D' − 2) z = 0 i.e., (D − (−1) D' − 2] z = 0 We know that, working rule case (i) is If (D - m D' - c) z = 0, then z = ecx f(y+mx) where ƒ is arbitrary. Example 1.5.35 : Solve (D + D′ − 2) (D + 4 D' − 3 ) z = 0 Solution: Given: (D + D' - 2) (D + 4D' − 3) z = 0 i.e., [D − (−1) D' − 2 ] [ D − (−4) D' — 3] z = 0 We know that, working rule case (ii) is Example 1.5.36 : Solve : (D2 – DD' + D' − 1) z′ = 0 Solution : Another method : Example 1.5.37 : Solve : (2 DD' + D'2 – 3D′) z = 3 cos (3x — 2y) Solution : To find the complementary function Another method to find C.F. Example 1.5.38 : Solve (D − D' − 1) (D − D' − 2) z = e2x−y Solution : To find C.F. take (D − D' − 1) (D − D' − 2) z = 0 by working rule case (ii) Example 1.5.39: Solve (D − D' − 1) (D − D' — 2) z = e2x+y Solution: Given: (D − D' − 1) (D − D' - 2) z = e2x+y To find C.F. (D − D' − 1) (D − D' – 2) z = 0 by working rule case (ii) Example 1.5.40 : Solve (D + D' − 1) (D + 2D' − 3) z = 4 + 3x + 6y. Solution : Given (D + D' − 1) (D + 2D' - 3) z = 4 + 3x + 6y To find C.F. (D + D' − 1) (D + 2D' - 3) z = 0 (D − (−1) D' − 1) (D − (−2) D' - 3) z = 0 by working rule case (ii) Example 1.5.41: Solve (D + 3D' + 4)2 z = 0 Solution: Given: (D + 3D' + 4)2 z = 0 (D − (−3) D' − (−4)]2 z = 0 by working rule case (iii) Example 1.5.42 : Find the general solution of (D2 - 3DD' + 2D'2 + 2D − 2D') z = sin (2x + y) Solution: Given: (D2 – 3DD' + 2D'2 + 2D - 2D') z = sin (2x+y) EXERCISES Answers:1. Partial differential equation of Higher order

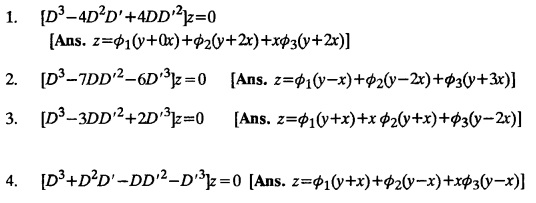 2. Homogeneous linear equation
2. Homogeneous linear equation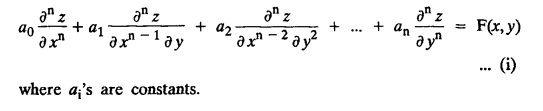



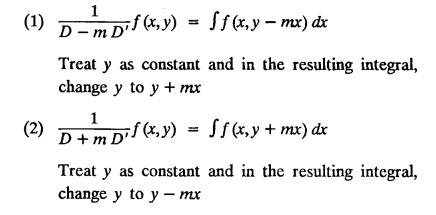
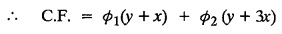
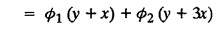
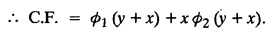
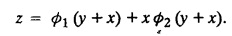
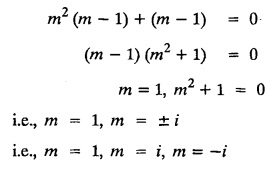
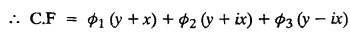
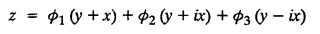
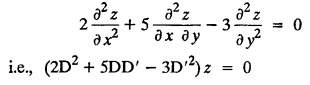
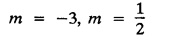
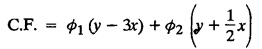
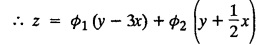
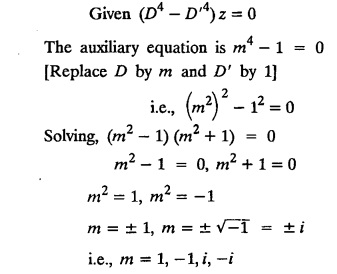
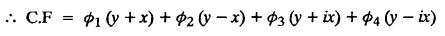
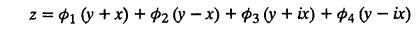
EXERCISES

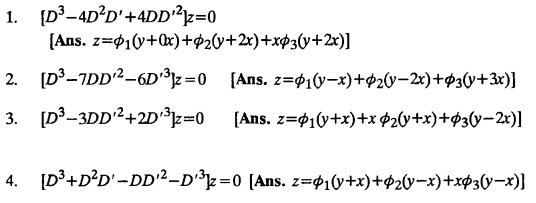
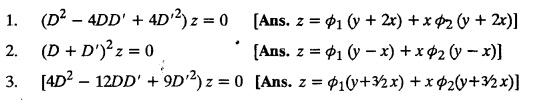
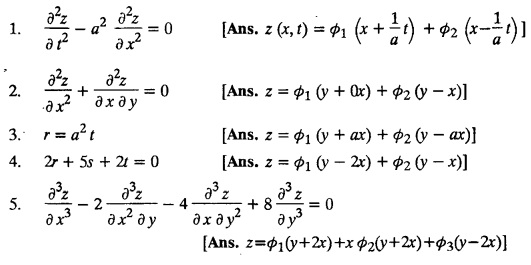
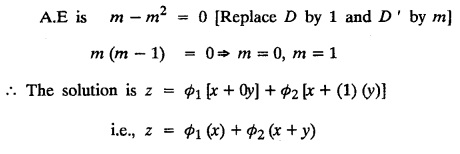
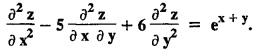
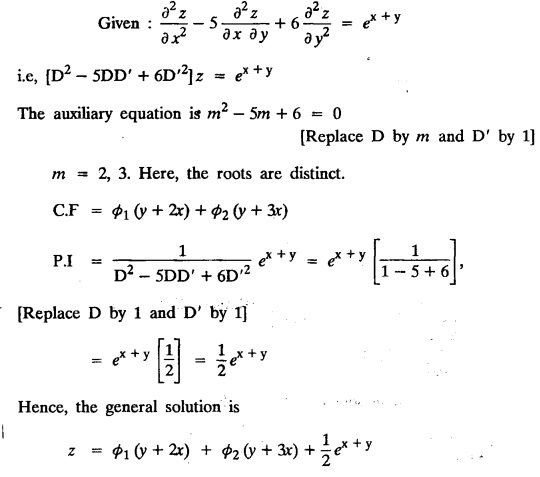
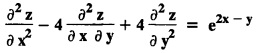
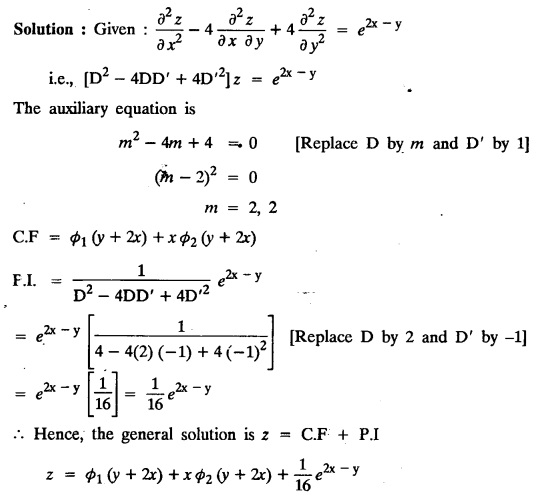


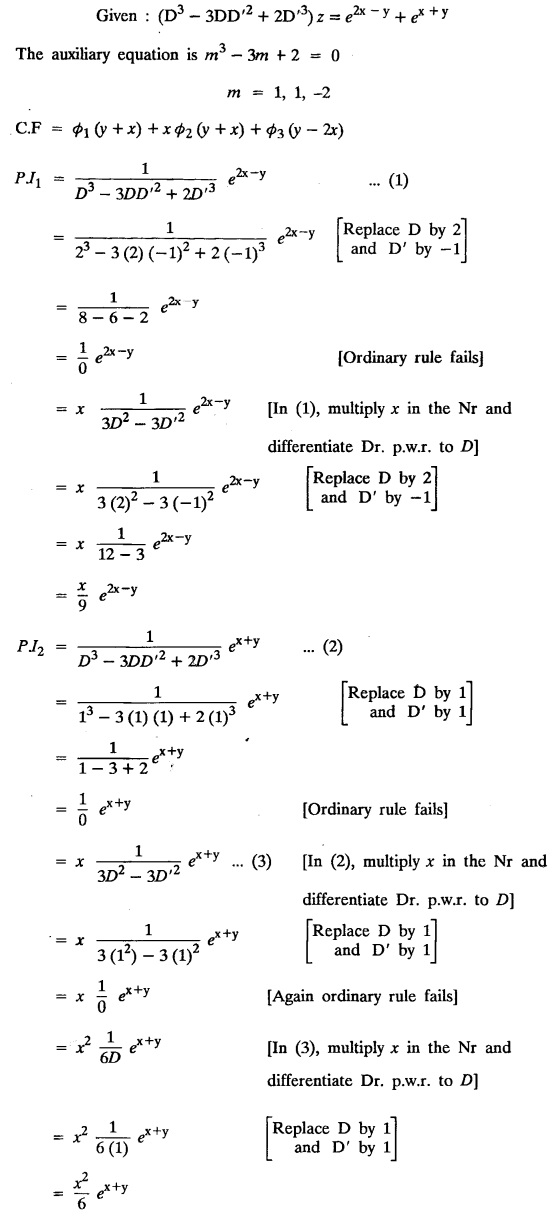
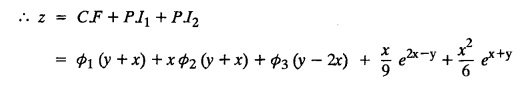
EXERCISES
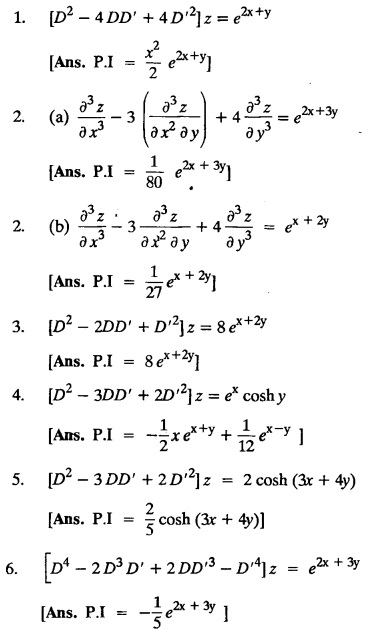
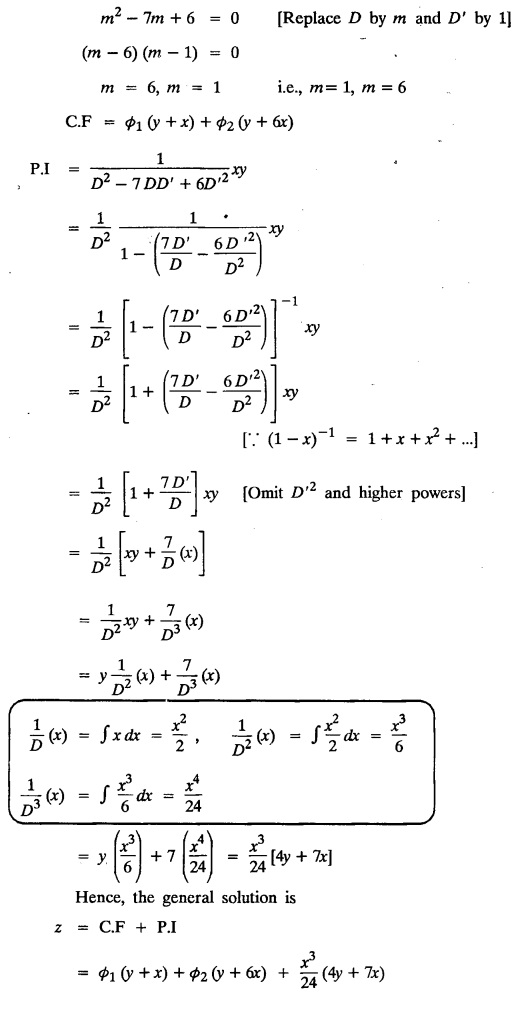
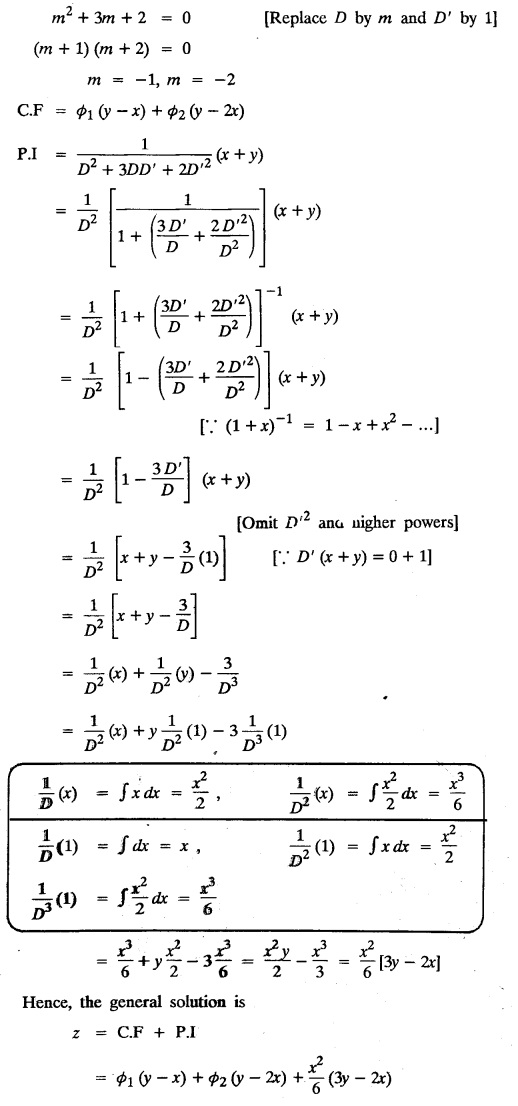
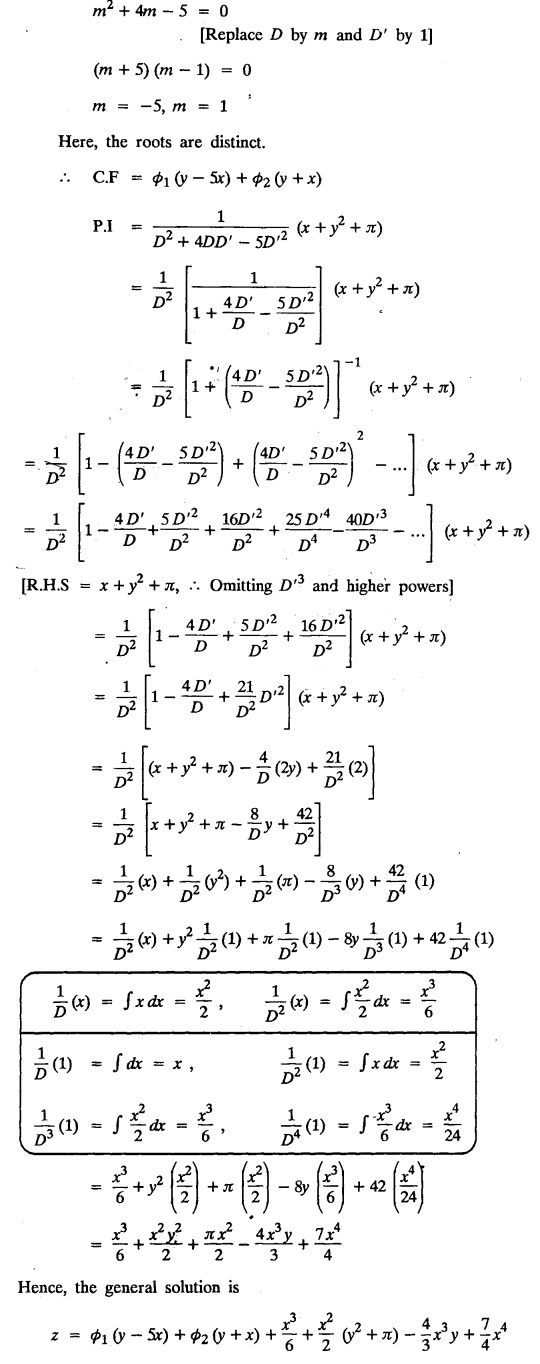
EXERCISES





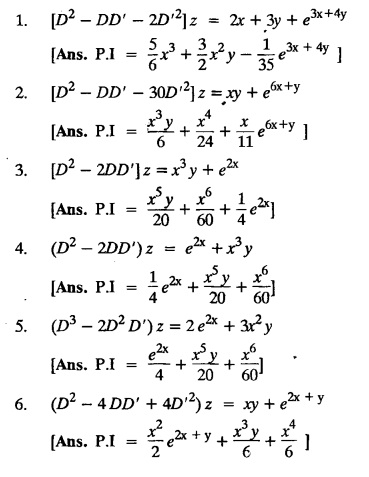
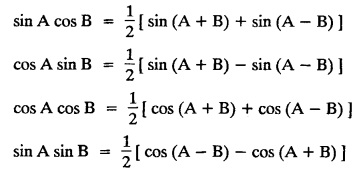

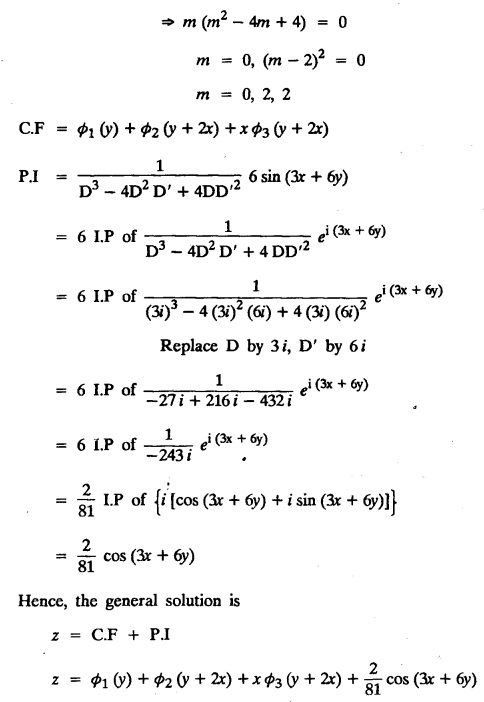

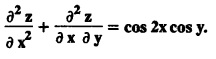



EXERCISES
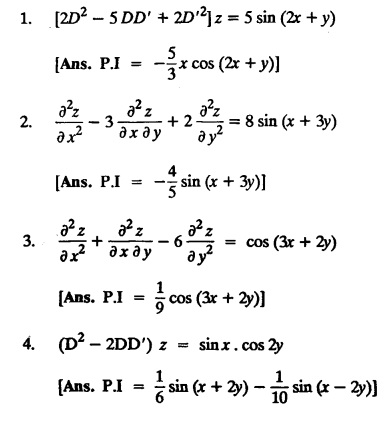
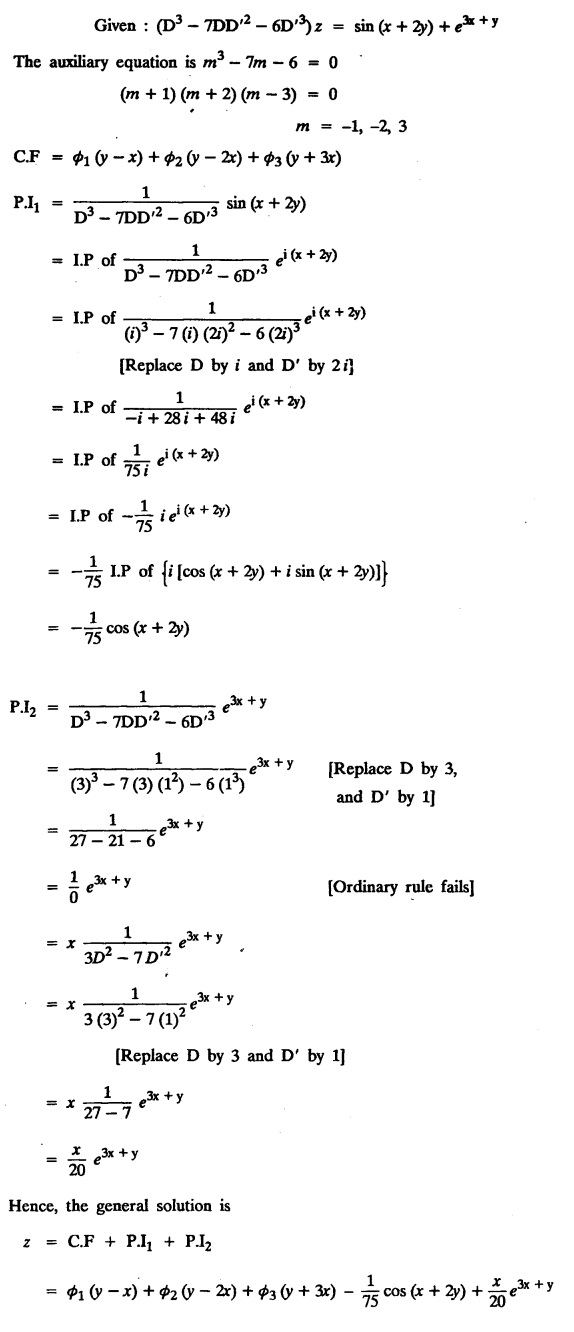
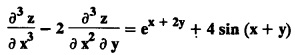
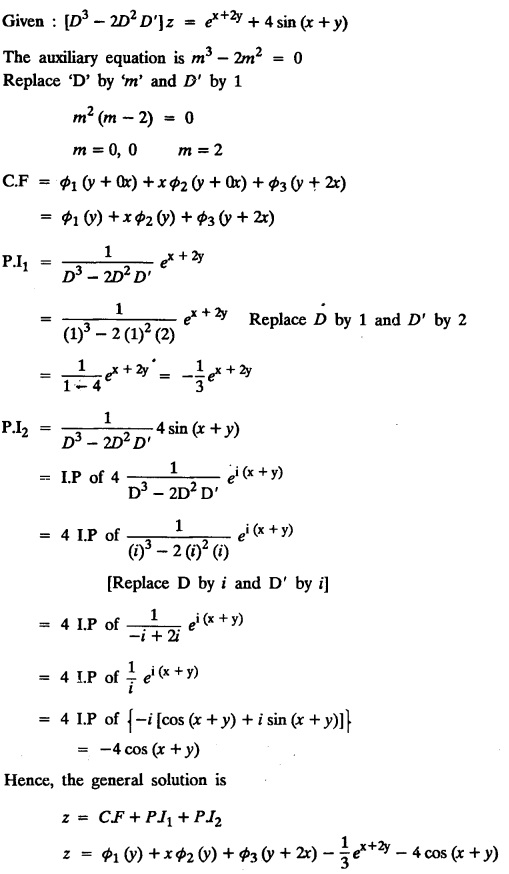
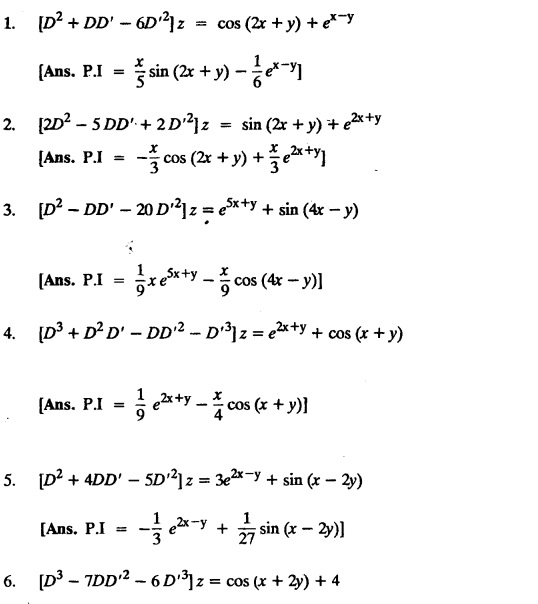

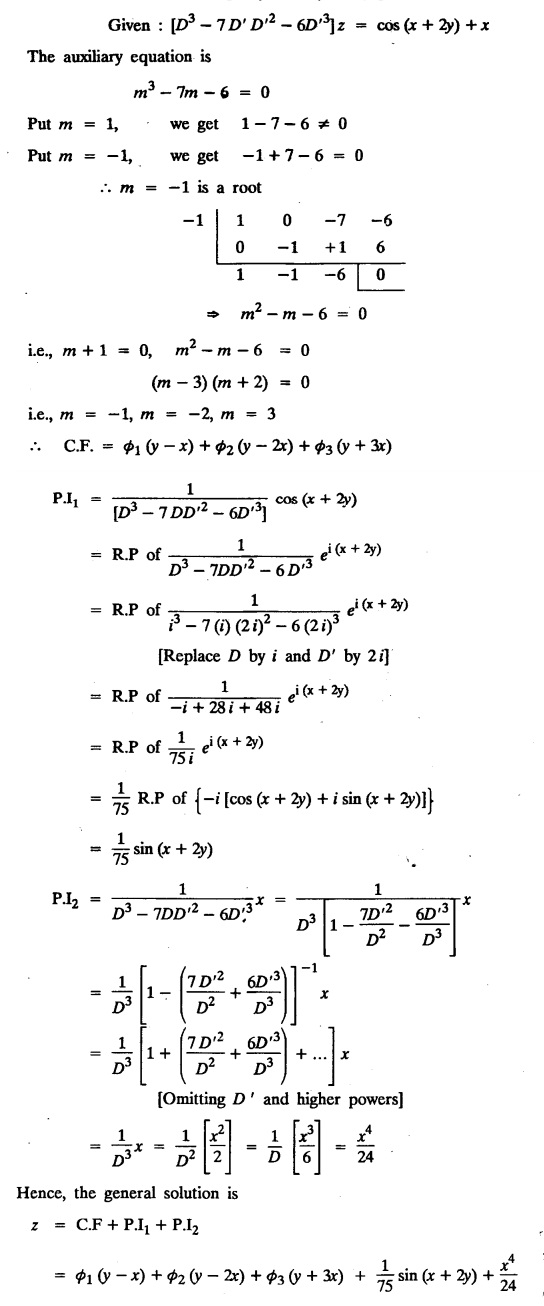

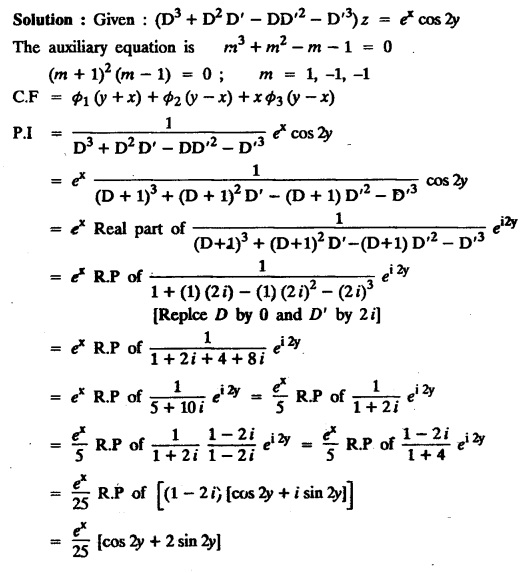
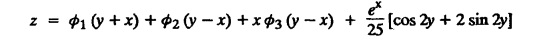
EXERCISES
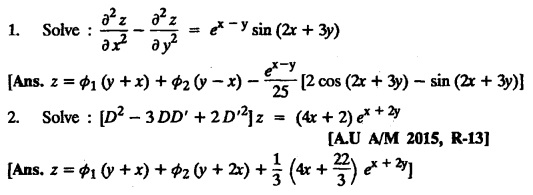
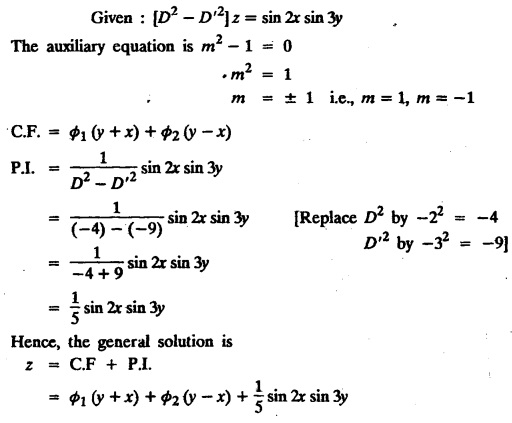
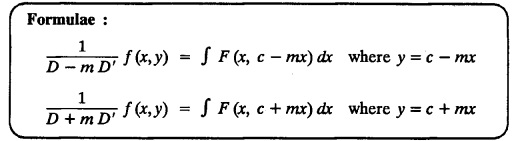
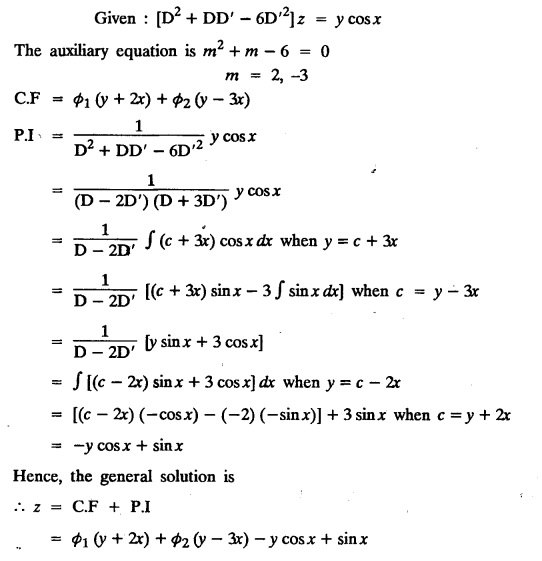
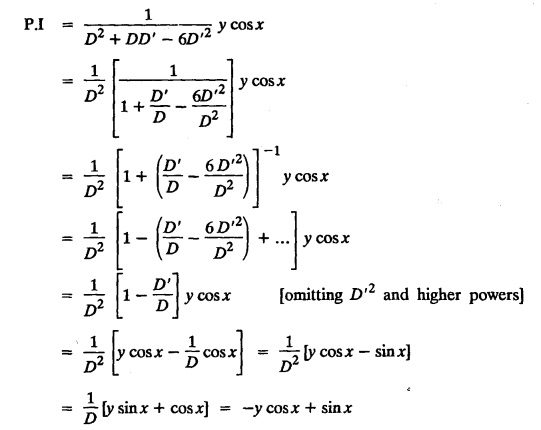
EXERCISES
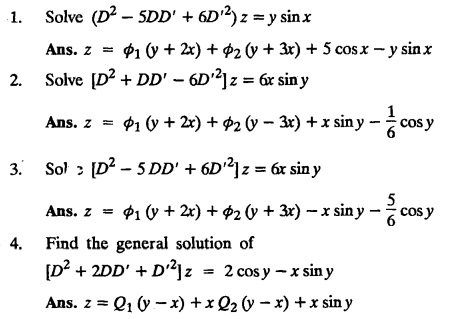
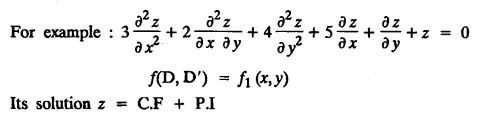

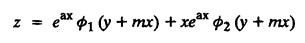
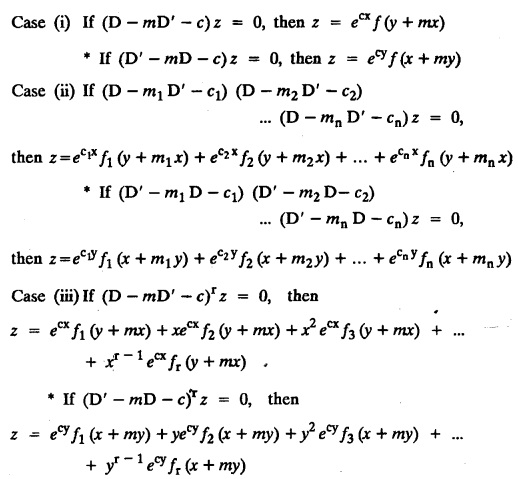
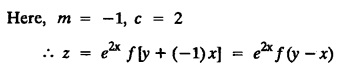
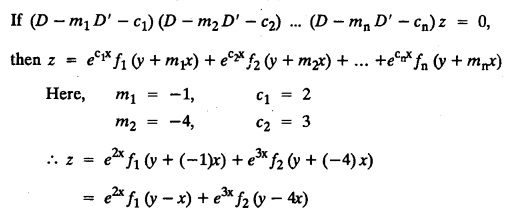
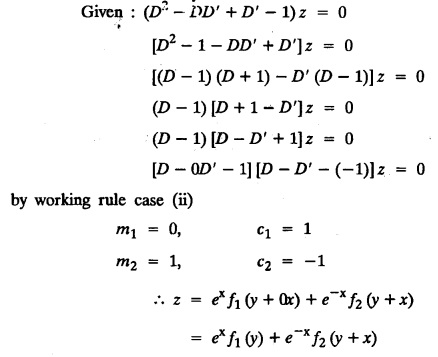


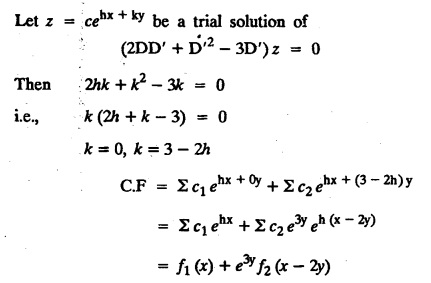
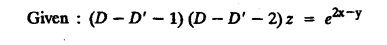
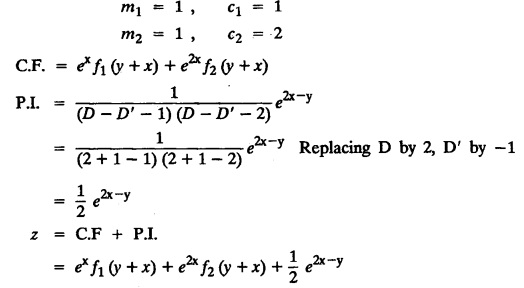
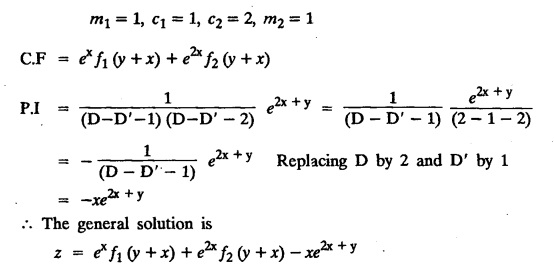
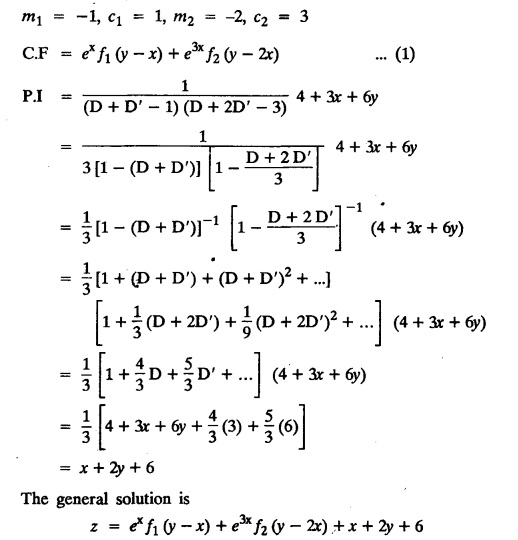
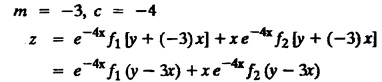
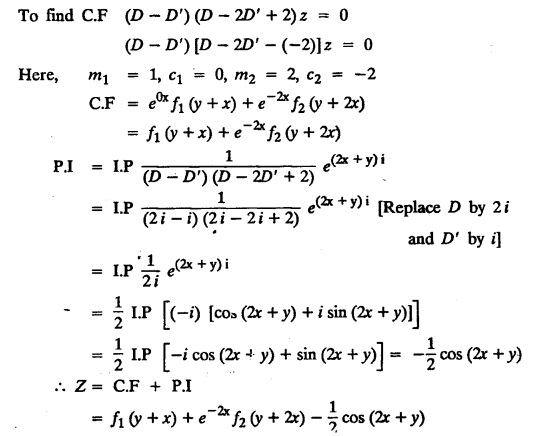
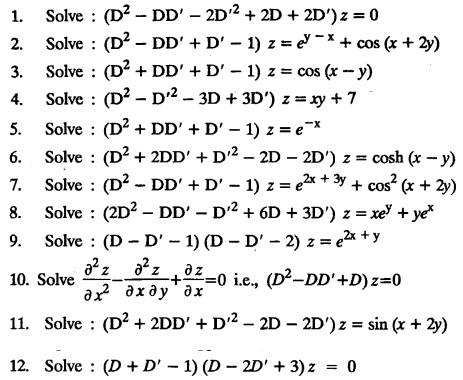

Transforms and Partial Differential Equations: Unit I: Partial Differential Equations : Tag: : Solved Example Problems - Linear partial differential equations of second and higher order with constant coefficients of both homogeneous and non-homogeneous types
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
