Matrices and Calculus: Unit III: Functions of Several Variables
Limit and Continuity
Definition, Worked Examples, Exercise with Answers
Let S be subset of R2. A function f: S→ R is a rule which assigns to every (x, y) ∈ S a unique real number in R, denoted by f(x, y).
LIMIT AND CONTINUITY Definition 3.1.1 Function of two variables Let S be subset of R2. A function f: S→ R is a rule which assigns to every (x, y) ∈ S a unique real number in R, denoted by f(x, y). We say f(x, y) is a function of two independent variables x and y. S is called the domain of the function f. Example 1 If f(x, y) = Solution Domain of ƒ is the set of all points in the plane at which f(x, y) exists. f(x, y) is defined for all x ≠ y So domain D = {(x, y) ∈ R2 | x ≠ y} Geometrically, D is the xy-plane, except the line y = x. Definition 3.1.2 The δ -neighbourhood of the point (a, b) is the disc A neighbourhood may also be taken as a square 0 < |x − a| < δ, 0 < | y − b| < δ Definition 3.1.3 Let f be a function defined on S ⊂ R2. The function f is said to tend to the limit l as (x, y) → (a, b) if to every ɛ > 0, ∃ δ > 0, such that |f(x, y) − l < ɛ, for all (x, y) satisfying ||(x, y) − (a, b)|| < δ This limit is called the double limit or simultaneous limit of f(x, y) Note (1) If for every (x, y) ∈ S ⊂ R2, there is a unique z assigned by f, then z = f(x, y). Geometrically this represents a surface. (2) If (3) To test limit f(x, y) does not exist. If l1 ≠ l2, then the limit of the function does not exist. Example 2 Solution This depends on m and so for different values of m, we will get different limit values. Hence the limits along different paths are different. ⸫ the limit does not exist. Note The existence of Definition 3.1.4 If f(x, y) is defined in a neighbourhood of (a, b) and if Similarly, we can definite the repeated limit Remark If the double limit (2) If the double limit exist and repeated limits exist, then they are equal. That is Example 3 If f(x, y) = Solution Since the repeated limits are unequal, double limit does not exist. Definition 3.1.5 A function f(x, y) is said to be continuous at (a, b) if Example 1 Text the continuity of the function at the origin. Solution Hence f(x, y) is continuous at (0, 0). Example 2 Solution The limit depends on m and so for different values of m, we get different limits. Hence the limit does not exist. Example 3 Find the limit and test for continuity of the function. Solution By the definition of the function ƒ(0, 0) = 0 Since the limit depends on m, for different values of m, we will have different limit values. Hence limit does not exist. ⸫ The function is not continuous at (0, 0). 1. Evaluate the following limits, if they exist. 2. Test continuity of the following 1. (i) does not exist. (ii) does not exist (iii) does not exist. 2. (i) not continuous (ii) not continuous [Hint limit does not exist. Choose paths y = x, x = y3] (iii) not continuous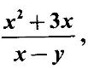 find the domain and ƒ(1, 3).
find the domain and ƒ(1, 3).
Neighbourhood of a point in the plane

Limit of a function

 f(x, y) = l and if y = φ (x) is a function such that φ (x)→ b
f(x, y) = l and if y = φ (x) is a function such that φ (x)→ b 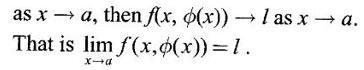
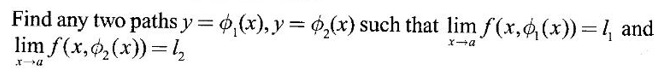


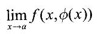 does not imply the existence of
does not imply the existence of
Repeated limits or iterated limits
 exists, then the limit is a function of y and the limit as y → b is written as
exists, then the limit is a function of y and the limit as y → b is written as 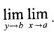 f(x, y). This limit is called repeated limit of f(x, y) as x → a a first and then as y → b.
f(x, y). This limit is called repeated limit of f(x, y) as x → a a first and then as y → b.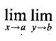 f(x, y). The two repeated limits may or may not exist and when they exist, they may or may not be equal. Even if the repeated limits have the same value, the double limit may not exsist.
f(x, y). The two repeated limits may or may not exist and when they exist, they may or may not be equal. Even if the repeated limits have the same value, the double limit may not exsist.![]() f(x, y) exists, then we cannot say repeated limits exist. But if the repeated limits exist and are not equal, then the double limit cannot exist.
f(x, y) exists, then we cannot say repeated limits exist. But if the repeated limits exist and are not equal, then the double limit cannot exist.
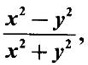 where (x, y) ≠ (0, 0), find the repeated limits and double limit, if they exist
where (x, y) ≠ (0, 0), find the repeated limits and double limit, if they exist
Continuity of a function
 f(x, y) = f(a, b)
f(x, y) = f(a, b)WORKED EXAMPLES


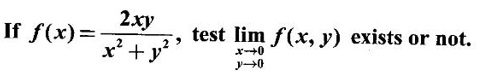

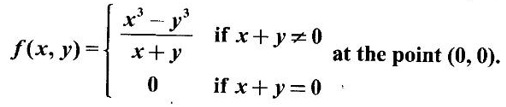


EXERCISE 3.1

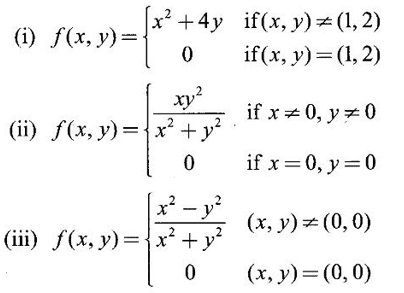
ANSWERS TO EXERCISE 3.1
Matrices and Calculus: Unit III: Functions of Several Variables : Tag: : Definition, Worked Examples, Exercise with Answers - Limit and Continuity
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
