Theory of Machines: Unit II: Gears and Gear Trains
length of path of contact
Gears and Gear Trains - Theory of Machines
Fig.4.23 shows two involute gears i.e., pinion and wheel in mesh.
LENGTH OF PATH OF CONTACT • Fig.4.23 shows two involute gears i.e., pinion and wheel in mesh. • When the pinion (driver) rotates in clockwise direction, the contact between a pair of teeth begins at point K and ends at point L. Therefore the length of path of contact is KL. • Point K is located on the flank near the base circle of pinion or the outer end of the tooth face on the wheel. Similarly, point L is on the flank near the base circle of pinion. MN is the common tangent... • The point K is the intersection of the addendum circle of wheel and the common tangent. The point L is the intersection of the addendum circle of pinion and the common tangent. • The lengths KP and PL are known as the path of approach and path of recess respectively. The total length KL is called the path of contact. Let r = O1 P = Pitch circle radius of pinion, R = O2P = Pitch circle radius of wheel, rA = O1 L = Addendum circle radius of pinion, and RA = O2K = Addendum circle radius of wheel. From Fig.4.23, the radius of the base circle of pinion is given by O1M = O1P cos ϕ = r cos ϕ and radius of the base circle of wheel, O2N = O2P cos ϕ = R cos ϕ From right angled triangle O2KN, ⸫ Length of path of approach is given by Similarly from right angled triangle O1ML, ⸫ Length of path of recess is given by Then, length of the path of contact is given by Substituting the values of KP and PL from equations (4.8) and (4.9), we get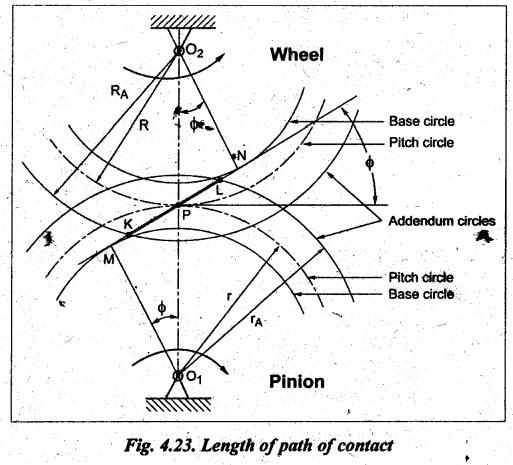


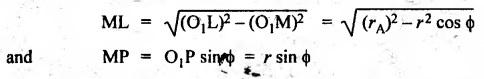
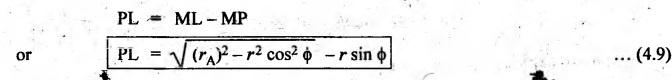


Theory of Machines: Unit II: Gears and Gear Trains : Tag: : Gears and Gear Trains - Theory of Machines - length of path of contact
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
