Theory of Machines: Unit II: Gears and Gear Trains
law of gearing (conditions of correct gearing)
Gears and Gear Trains - Theory of Machines
The law of gearing states the condition which must be fulfilled by the gear tooth profiles to maintain a constant angular velocity ratio between two meshing gears throughout the mesh.
LAW OF GEARING (Conditions of Correct Gearing) • The law of gearing states the condition which must be fulfilled by the gear tooth profiles to maintain a constant angular velocity ratio between two meshing gears throughout the mesh. • Law of gearing: The law of gearing states that for maintaining constant angular velocity ratio between two meshing gears, the common normal of the tooth profiles, at all contact points within mesh, must always pass through a fixed point on the lines of centres, called pitch point. Proof: Consider portions of two gears 1 and 2 such that gear 1 rotates at a speed of w about its axis O1 while gear 2 rotates with speed ω2 about the axis O2, as shown in Fig.4.17. • Why should the meshing gear maintain constant angular velocity ratio? • We know that the gear drive is a positive drive, which means gear drive should transmit an absolute uniform angular velocity ratio during even a small fraction of a revolution. • If the constant angular velocity ratio is not maintained, very serious vibration and impact problems would result, even at low speeds. Let at any instant, K may be their common point of contact. Draw a common tangent TT at the point of contact K. Also draw a normal N1N2 to the tangent at K which intersects the line connecting the two axes of rotation at P, as shown. Join O1 with K and from O1, draw a perpendicular O1M. Similarly, for gear 2, join O2 with K. Then draw a perpendicular O2N. Let v1 and v2 be the velocities at the point of contact K of the gears 1 and 2 respectively. Then v1 = ω1 × O1 K and v2 = ω2 × O2 K If the two gears 1 and 2 are always to remain in contact, the components of v1 and v2 along the line of transmission of motion (i.e., along the common normal N1N2) must be equal at any instant. But from ∆O1 MK and ∆O2NP, we get Substituting the values of cos α and cos β in the equation (i), we have Thus the ratio of angular velocities (ω1/ ω2) varies inversely with the ratio of distances of point P from centres O1 and O2. It should be noted the ratio (ω1/ ω2) will remain constant as long as the position of point P is fixed along the line O1 O2. Conclusion: Therefore, in order to have a constant angular velocity ratio for all positions of the gears, the common normal at the point of contact between a pair of teeth must always pass through the pitch point. In other words, any tooth shape should fulfill the following conditions for the velocity ratio to remain constant: (i) The path of gear contact is along a straight line known as line of action. (ii) The line of action should pass through the pitch point. (iii) The pitch point must remain stationary on the line of centres. • Velocity of sliding is the velocity of one tooth relative to its mating tooth along the common tangent at the point of contact. • Referring to Fig.4.17, we can write Component of v1 in the direction of the common tangent TT = v1 sin α Component of v2 in the direction of the common tangent TT = v2 sin β ⸫ Relative velocity of sliding of gear 2 with respect to gear 1, From equation (4.7), the following points may be observed. (i) The velocity of sliding is the product of sum of the angular velocity of the pair of gears and the distance of the point of contact from the pitch point. (ii) The maximum velocity of sliding occurs at the first (K) or at the last point (N) of contact along the line of action. (iii) The velocity of sliding is zero at the pitch point (P).

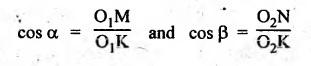

1. Velocity of Sliding of Teeth

Theory of Machines: Unit II: Gears and Gear Trains : Tag: : Gears and Gear Trains - Theory of Machines - law of gearing (conditions of correct gearing)
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
