Transforms and Partial Differential Equations: Unit I: Partial Differential Equations
Lagrange's Linear Equation
Solved Example Problems | Partial Differential Equations
The equation of the form Pp + Q q = R = R is known as Lagrange's equation when P, Q & R are functions of x, y and z.
LAGRANGE'S LINEAR EQUATION The equation of the form Pp + Q q = R = R is known as Lagrange's equation when P, Q & R are functions of x, y and z. To solve this equation it is enough to solve the subsidiary equation First step. Write down the subsidiary equations Second step: Solve the above subsidiary equations. Let the two solutions be u = a and v = b Third step Then f(u, v) = 0 or u = ϕ(v) is the required solution of P p + Qq = R Generally, the subsidiary equation can be solved in two ways. 1. Method of Grouping 2. Method of Multipliers 1. Method of Grouping In the subsidiary equation 2. Method of Multipliers Choose any three multipliers l, m, n which may be constants or function of x, y, z we have If it is possible to choose 1, m, n such that lP + mQ+ nR = 0 then ldx + mdy + ndz = 0 If ldx + mdy + ndz is an exact differential then on integration we get a solution u = a. The multipliers l, m, n are called lagrangian multipliers. 1.4a. Problems based on Lagrange's linear equation method of Grouping : Example 1.4a(1): Solve px + qy = z. Solution: Given: px + qy = z (i.e.,) xp + yq= z …..(1) This equation is of the form Pp + Qq = R where P = x, Q = y, R = z Example 1.4a(2): Write the solution of px2 + qy2 = z2. Solution: Given: px2 + qy2 = z2 i.e., x2p + y2q = z2 This equation is of the form P p + Q q = R where P = x2, Q = y2, R = z2 Example 1.4a(3) Find the solution of p√x + q√y = √z. Solution: Example 1.4a(4) : Find the general solution of p tan x + q tan y = tan z. Solution : Example 1.4a(5): Write the general integral of pyz + qzx = xy. Solution: Given: pyz + qzx = xy (i.e.,) yzp + zxq = xy This equation is of the form Pp + Qq = R where P = yz, Q = zx, R = xy The Lagrange's subsidiary equations are Hence, the general solution is ƒ (u, v) = 0 i.e., f (x2 - y2, y2 - z2) = 0, where ƒ is arbitrary. Example 1.4a(6) : Find the general integral of p − q = log (x + y). Solution : Example 1.4a (7): Obtain the general solution of pzx+qzy = xy. Solution: Example 1.4a(8) : Solve :y2 p - xyq = x (z − 2y) Solution: Example 1.4.a(9): Solve x2p + y2 q = z Solution: Solve the following : 1.4.b. Problems based on Lagrange's method of multipliers Example 1.4b(1): Solve x (y-z) p + y (z - x) q=z (x − y). (OR) Solve Solution: Given: x (y − z) p + y (z − x) q = z (x − y) This equation is of the form P p + Q q = R Taking the Lagrangian multipliers are 1, 1, 1, we get each ratio in (1) Hence, d(x + y + z) = 0 Integrating, we get x + y + z = a Taking the Lagrangian multipliers 1/x, 1/y, 1/z, we get each ratio in (1) Integrating, we get logx + logy + log z = log b log (xyz) = log b xyz = b Hence, the general solution is f (a, b) = 0 i.e., f (x + y + z, xyz) = 0 where f is arbitrary. Example 1.4b(2): Solve (mz - ny) p + (nx - lz) q = ly - mx. Solution: Given : (mz - ny) p + (nx - lz) q = ly - mx This equation is of the form Pp + Qq = R Taking the Lagrangian multipliers are x, y, z, we get each ratio in (1) Hence, xdx + ydy + zdz = 0 Integrating, we get Taking the Lagrangian multipliers are 1, m, n, we get each ratio in (1) Hence, ldx + mdy + ndz = 0 Integrating, we get lx + my + nz =b lx + my + nz = b Hence, the general solution is ƒ (a, b) = 0 i.e., f(x2 + y2 + z2, lx + my + nz) = 0, where ƒ is arbitrary. Example 1.4b(3): Solve (3z - 4y) p + (4x-2z) q 4y) p + (4x - 2z) q = 2y - 3x. Solution: Use Lagrangian multipliers x, y, z, we get each ratio in (1) Again use Lagrangian multipliers 2, 3, 4, we get each ratio in (1) Hence, the general solution is f (a, b) = 0 i.e., f(x2 + y2 + z2, 2x + 3y + 4z) = 0, where ƒ is arbitrary. Example 1.4b(4) Find the general solution of x2 (y2 – z2 ) p + y (z2 − x2) q = z (x2 − y2) (or) x (z2 − y2) p + y (x2 − z2) q = z (y2 − x2) Solution: Use Lagrange multipliers x, y, z, we get each ratio in (2) logx + logy + log z = log b log (xyz) = log b i.e., xyz = b Hence, the general solution is ƒ (a, b) = 0 i.e., f (x2 + y2 + z2, xyz) = 0, where f is arbitrary. Example 1.4b(5): Solve (x2 - yz) p + (y2 − zx) q = (z2 − xy). Solution: a = x2 + y2 + z2 − (x + y + z)2 = x2 + y2 + z2 - x2 - y2 - z2 - 2xy - 2yz - 2zx = -2 (xy + yz + zx) Using two sets of multipliers 1, −1, 0; 0, 1, −1 each of the ratio in (2). Integrating on both sides, we get log (x − y) = log (y - z) + log b log (x − y) = log [b (y - z)] x – y = b (y - z) Aliter: Using Lagrange multipliers y + z, z + x, x + y we get each ratio in (2) Note: The author wishes to thank Dr. B. Jothiram, formerly Asst. Prof. and HOD Maths, Govt. College of Engg., Salem, for having drawn his attention to this elegant method of getting one of the independent solutions. Example 1.4b(6): Solve (x2 + y2 + yz) p + (x2 + y2 − xz) q = z(x + y). Solution : Use Lagrange multipliers 1, -1, -1, we get each ratio in (1) Integrating, we get Integrating, we get Example 1.4b(7): Solve (y2 + z2) p – xyq + xz = 0 Solution: Use Lagrangian multipliers x, y, z, we get each ratio in (A) Example 1.4b(8): Solve : x (y2 + z) p + y (x2 + z) q = z (x2 - y2). Solution: This equation is of the form P p + Q q = R where P = x (y2 + z), Q = y (x2 + z), R = z (x2 - y2). The Lagrange's subsidiary equations are Taking the Lagrangian multipliers x, −y, −1, we get Hence, x dx - y dy - dz = 0 Integrating, we get Example 1.4b(9): Solve the equation: (x2 – y2 – z2) p + 2 xyq = 2 zx Solution: Choosing the method of multiplier idea x, y, z as multipliers. Example 1.4b(10): Solve (z2 - 2yz - y2) p + (xy + zx) q = xy - zx Solution: The Lagrange's subsidiary equations are Choose the multipliers x, y, z, we get. Hence, the general solution is ƒ (y2 - 2yz - z2, x2 + y2 + z2) = 0, where ƒ is arbitrary. Example 1.4b(11) : Solve (y + z) p + (z + x) q = x + y. Solution : Given (y + z) p + (z + x) q = x + y This equation is of the form Pp + Qq = R Hence, the general solution is ƒ (u, v) = 0 Example 1.4b(12): Solve (y-xz) p + (yz - x) q = (x + y) (x − y) Sol. Choose Lagrangian multipliers x, y, z, Choose Lagrangian multipliers y, x, 1, Example 1.4b(13) : Solve (y − z) p − (2x + y) q = 2x + z. Solution: Given: (y - z)p (2x + y) q = 2x + z This equation is of the form Pp + Qq = R where P = y – z, Q = -(2x + y), R = 2x + z The Lagrange's subsidiary equations are, Choose Lagrangian multipliers 1, 1, 1, Integrating, we get Example 1.4b(14): Show that the integral surface of the equation 2y (z − 3) p + (2x − z) q = y (2x - 3) that passes through the circle x2 + y2 = 2x, z = 0 is x2 + y2 – z2 − 2x + 4z = 0. Solution : Given: 2y (z - 3) p + (2x − z) q = y (2x − 3) This equation is of the form Pp + Qq = R The required surface has to pass through substitute for a and b from (2) and (3) in (9), we get x2 + y2 - z2 - 2x + 4z = 0 which is the equation of the required integral surface. EXERCISES 1.4.b Find the general solution of
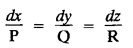
Working Rule
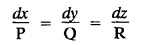
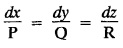 if the variables can be separated in any pair of equations, then we get a solution of the form u (x, y) = a and v (x, y) = b.
if the variables can be separated in any pair of equations, then we get a solution of the form u (x, y) = a and v (x, y) = b.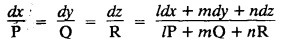

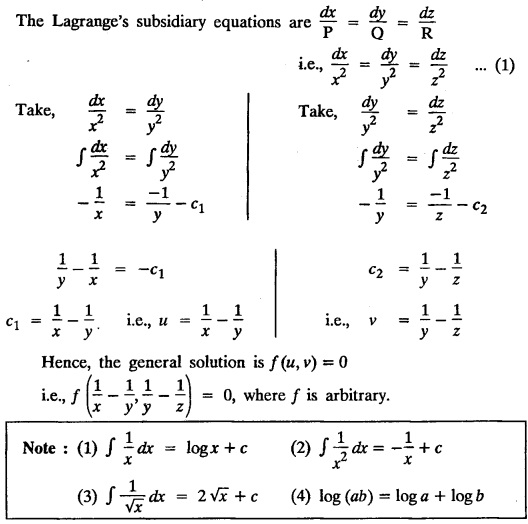


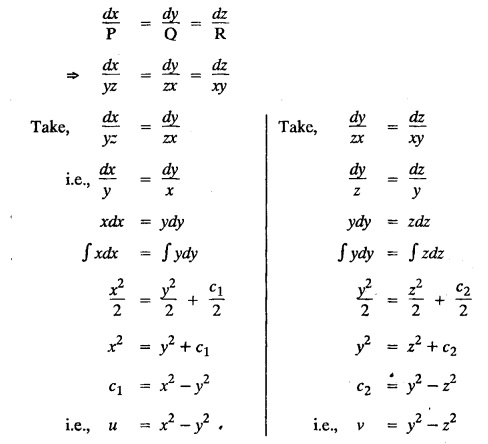


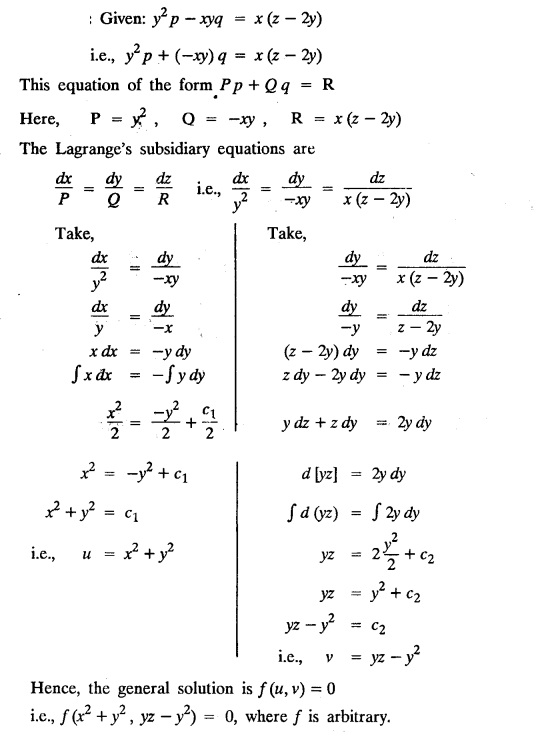

EXERCISES 1.4.a
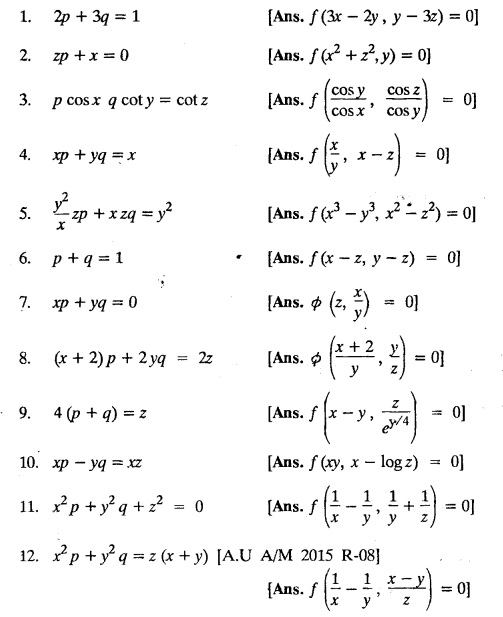
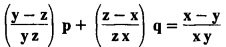
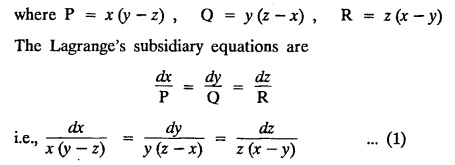

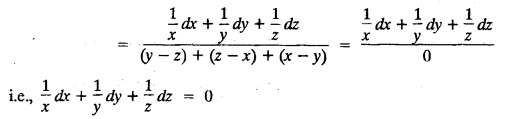
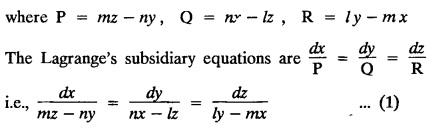
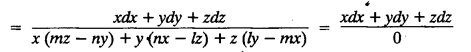
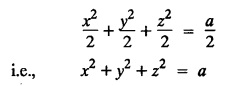
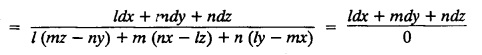
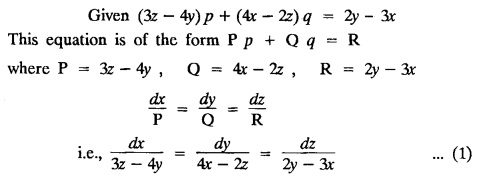
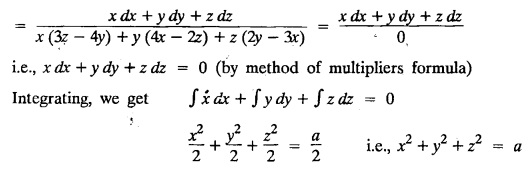

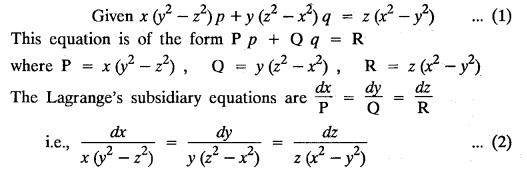


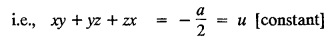
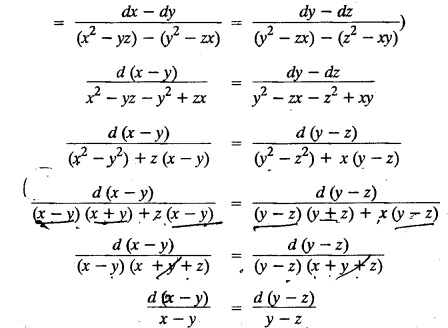
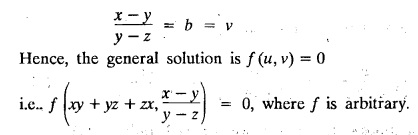
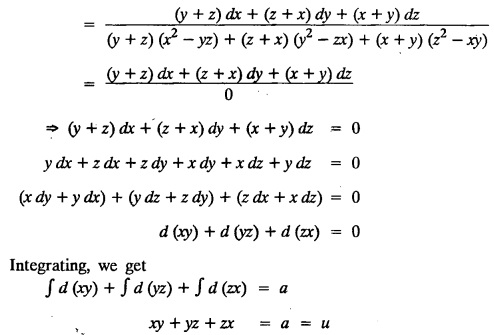

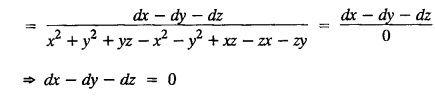



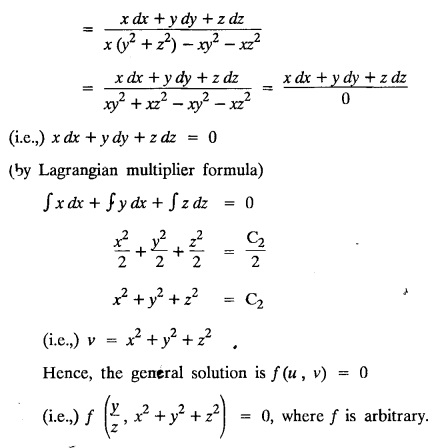

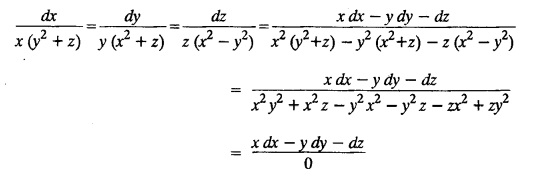



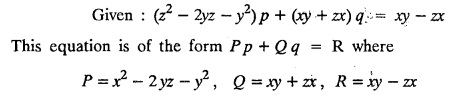
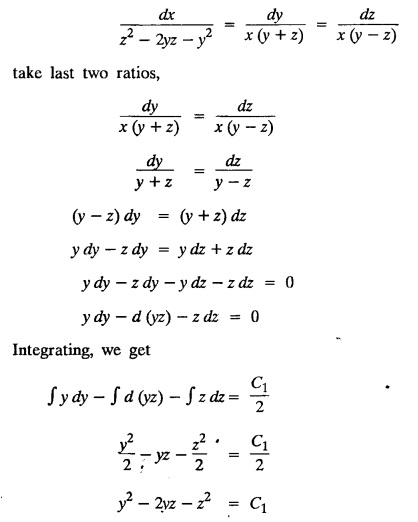
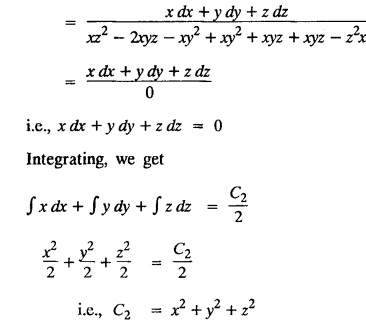

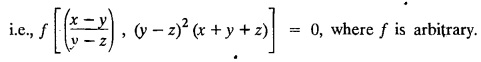
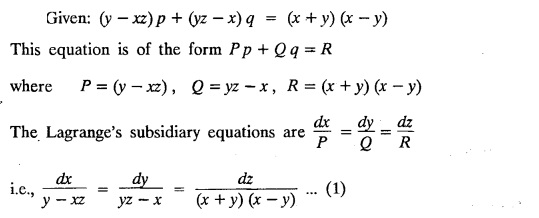
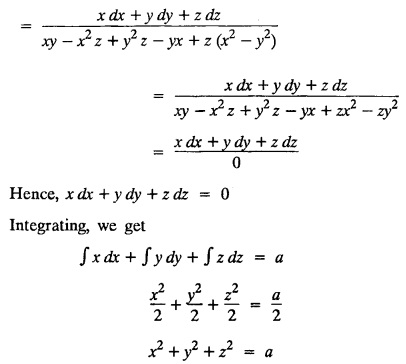
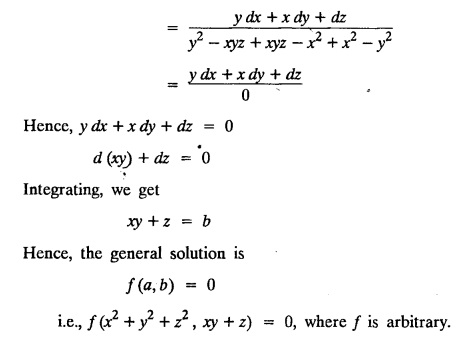
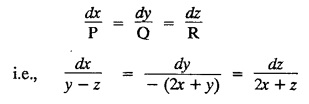

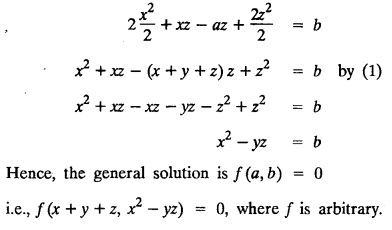

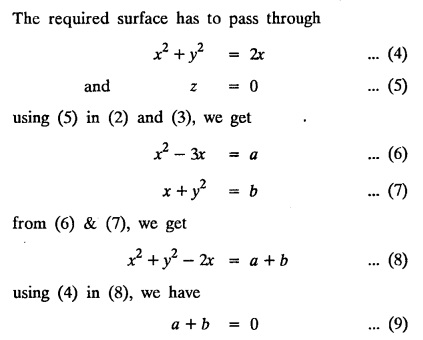

Transforms and Partial Differential Equations: Unit I: Partial Differential Equations : Tag: : Solved Example Problems | Partial Differential Equations - Lagrange's Linear Equation
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
