Engineering Mechanics: Unit V: Dynamics of Particles
Kinetics of Curvilinear Motion
with Solved Example Problems
If normal and tangential components are used, the equations of motion would be
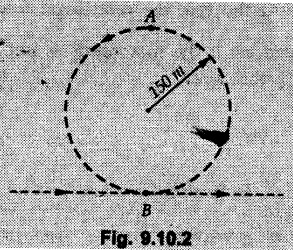
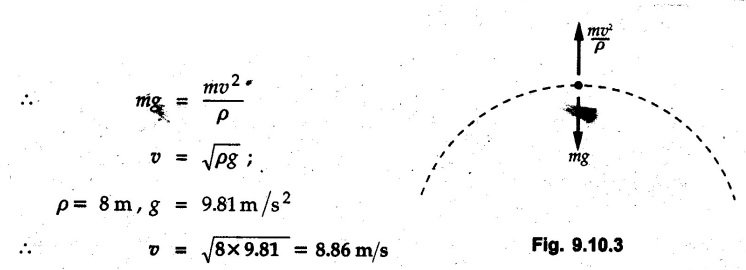
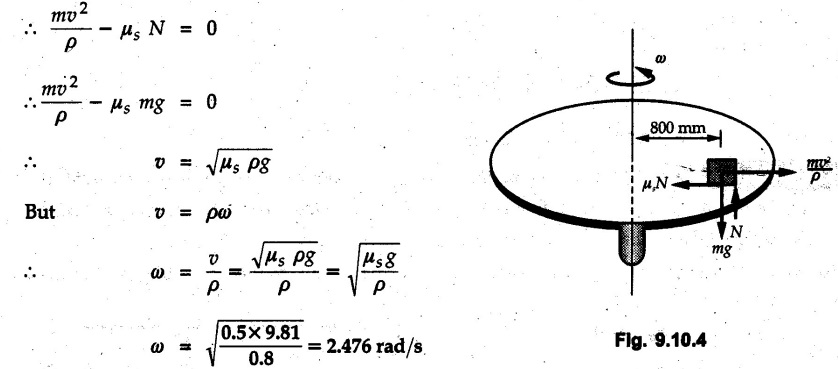
Kinetics of Curvilinear Motion • If normal and tangential components are used, the equations of motion would be man is called the centripetal force. • at, is directed along the tangent in the direction of velocity and an is directed towards the centre of curvature as shown in Fig. 9.10.1. • Another approach is to use dynamic equilibrium condition in which • In this book, we will be using the dynamic equilibrium equation for the normal direction, so that equations of motion will be where mv2/ρ the centrifugal force will be shown directed away from the centre of curvature. In many problems only equation (9.10.2) will be required. Draw F.B.D. of object. Resolve all forces in tangential and normal directions. Show centrifugal force directed away from the centre. If radial and transverse components are used, the equations of motion will be Example 9.10.1 A 70 kg pilot flies in a small plane which moves in a vertical loop of 150 m radius as shown. Knowing that pilot experiences weightlessness at ‘A’ and has apparent weight 2800 N at 'B', find speed of plane at 'A' and 'B'. Solution: The forces on the pilot in the normal direction at A and B are shown in Fig. 9.10.2 (a) and (b). The normal reaction is the apparent weight. Example 9.10.2 A motorcycle stuntman drives his motorcycle in a spherical cage in a vertical circle of radius 8 m. Determine the minimum velocity with which he should drive his motorcycle so that he does not lose contact with the cage at top of the circular path. Solution: At the top, the centrifugal force mv2/ρ must balance mg if the motorcycle is not to lose contact with the cage. Example 9.10.3 A concrete block is placed at 800 mm from axis of rotation on a turn table. If μs = 0.5 and If μk = 0.4 between the block and table, find maximum angular speed of turn table about its vertical axis that can be given without causing the block to slip. Solution: From FBD of block shown in Fig. 9.10.4. If the block is not slip Example 9.10.4 A 400 g sphere attached to a string is held in such a position that the string fixed in the horizontal ceiling makes an angle of 50° with ceiling. When released from this position, find tension in string and acceleration of sphere at this instant. Solution: v = 0 as sphere is released from rest. The forces acting on the sphere are as shown in Fig. 9.10.5. Example 9.10.5 A man of mass 60 kg is sitting in a car which is travelling in a circular path of radius 100 m. If μs = 0.5 between the seat and the man, find the velocity of the car at which he starts slipping. Solution: The centrifugal force mv2/ρ tries to make the man slip whereas the frictional force μs mg prevents slipping. Example 9.10.6 A man is standing at the centre of a revolving stage which is being rotated at the rate of 12 r.p.m. about a vertical axis. Find the distance from the centre upto which he can go radially outwards without slipping. Take μs = 0.5. Solution: When the man is at a distance p from the centre, the forces acting on the man are as shown in Fig. 9.10.6. Example 9.10.7 A cylindrical bowl of 500 mm radius rotates about its vertical axis. Find minimum angular speed in r.p.m. so that a small block placed on the wall of cylinder does not fall down. Assume μ = 0.30 between block and bowl. Solution : Let m = Mass of the block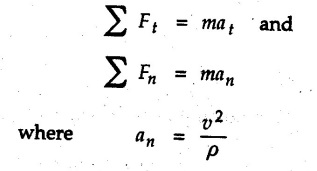

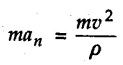 is shown directed away from the centre (the centrifugal force).
is shown directed away from the centre (the centrifugal force).
1. General Procedure for Solving Problems
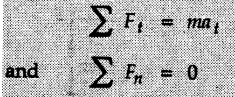

Solved Examples for Understanding




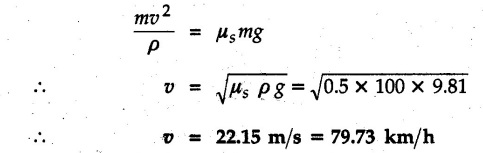



Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : with Solved Example Problems - Kinetics of Curvilinear Motion
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
