Engineering Mechanics: Unit V: Dynamics of Particles
Kinetics - Newton's second law of Motion
with Solved Example Problems
Kinetics is the study of motion of bodies by considering the forces acting on them. In rectilinear motion, acceleration is caused by unbalanced force.
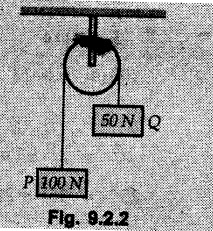
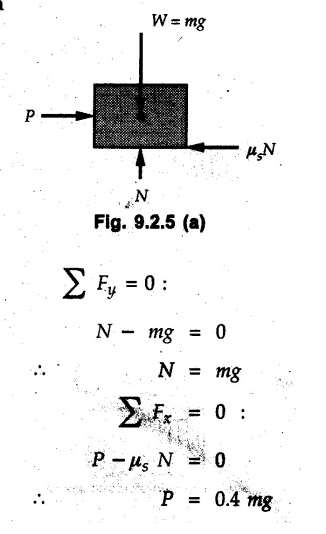
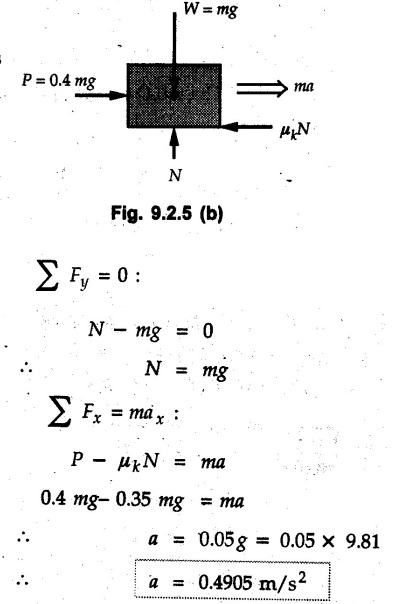
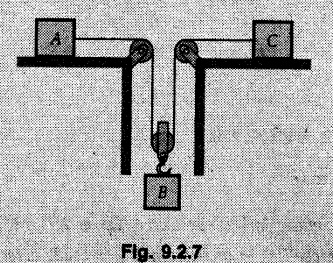
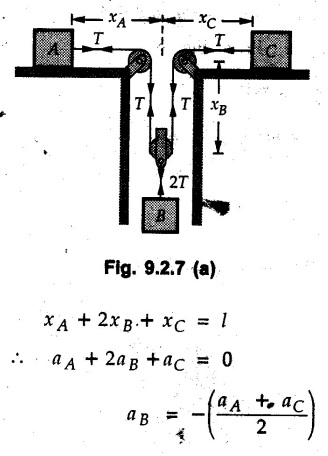
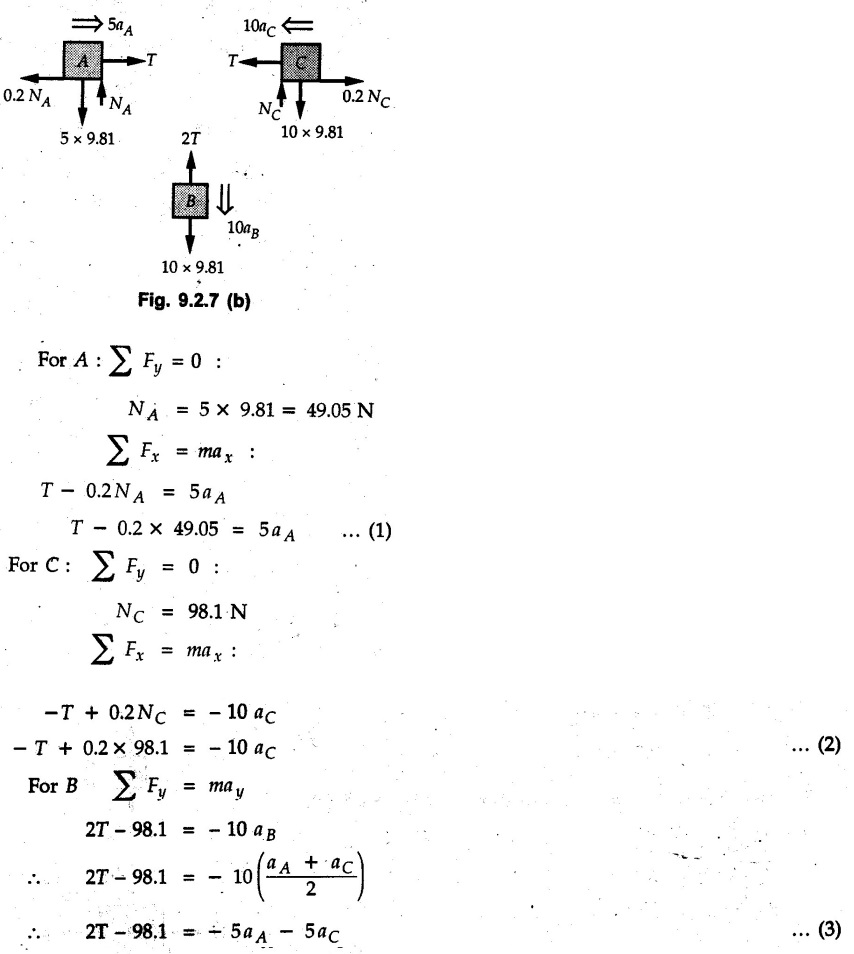
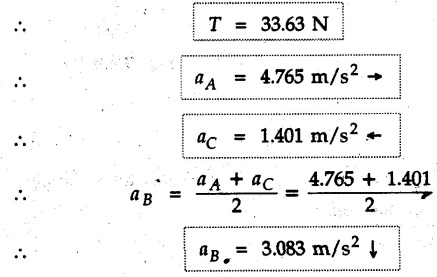
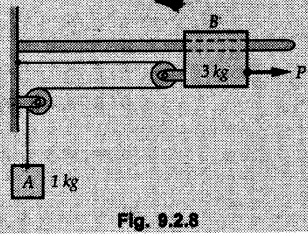
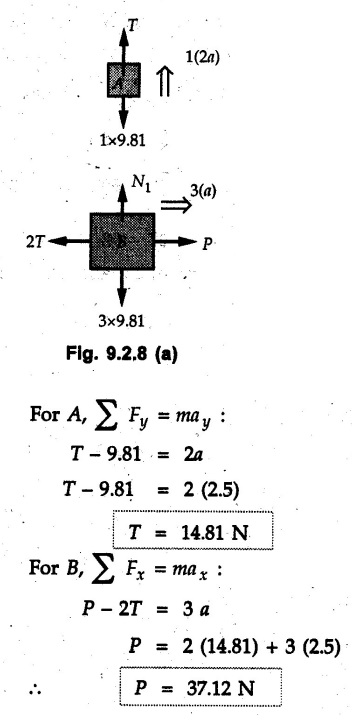
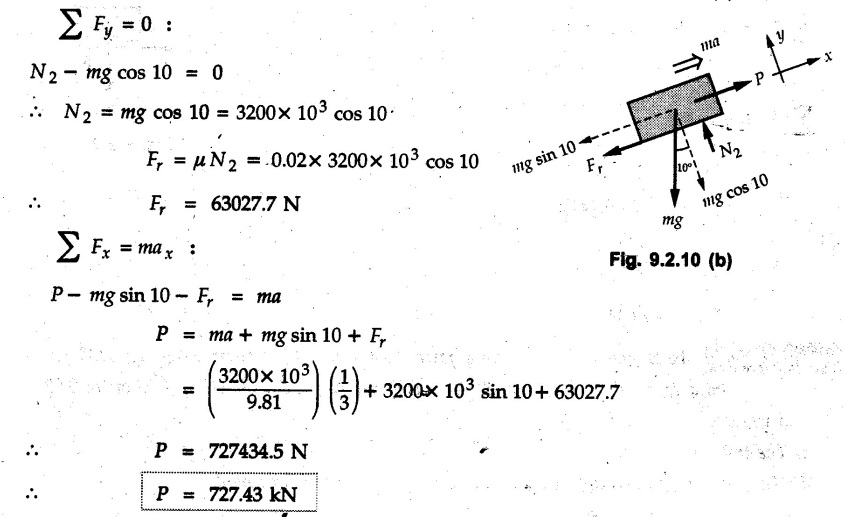
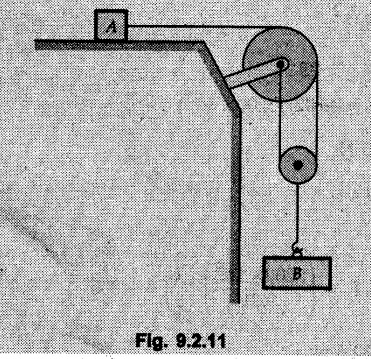
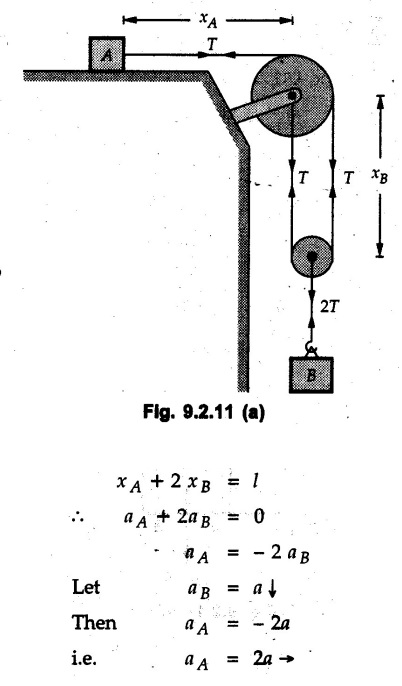
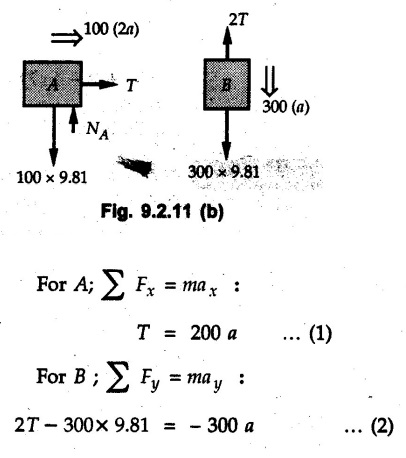
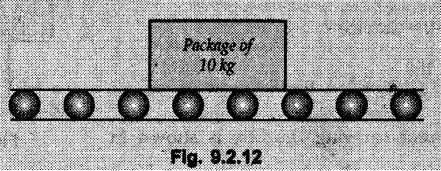
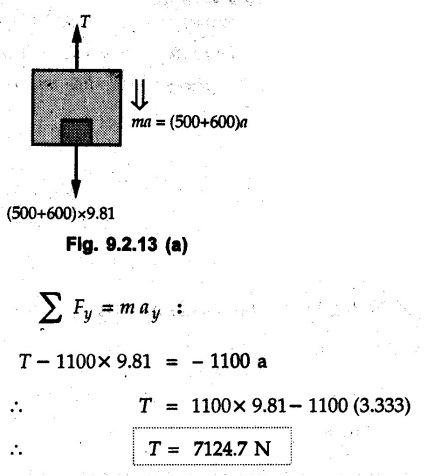
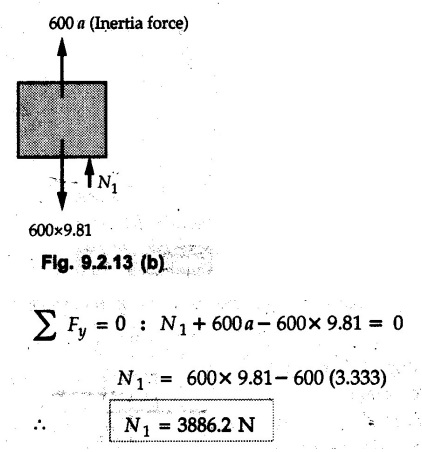
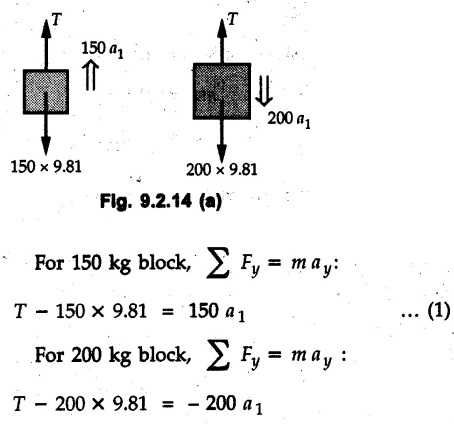
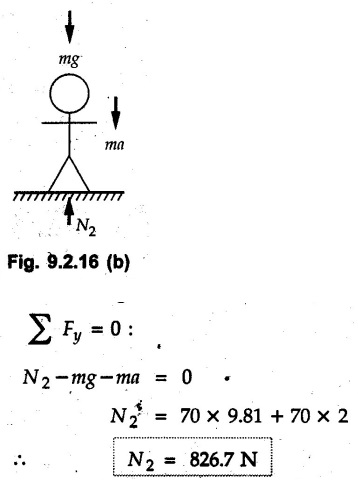
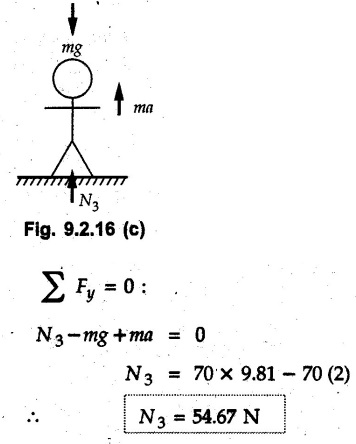
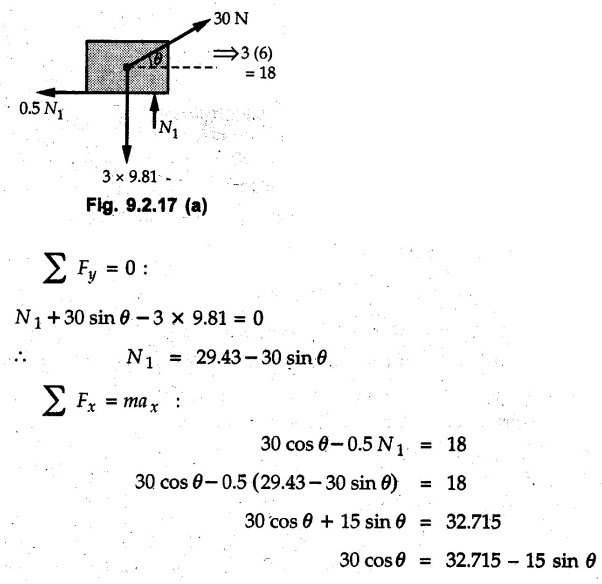
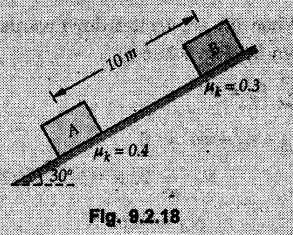
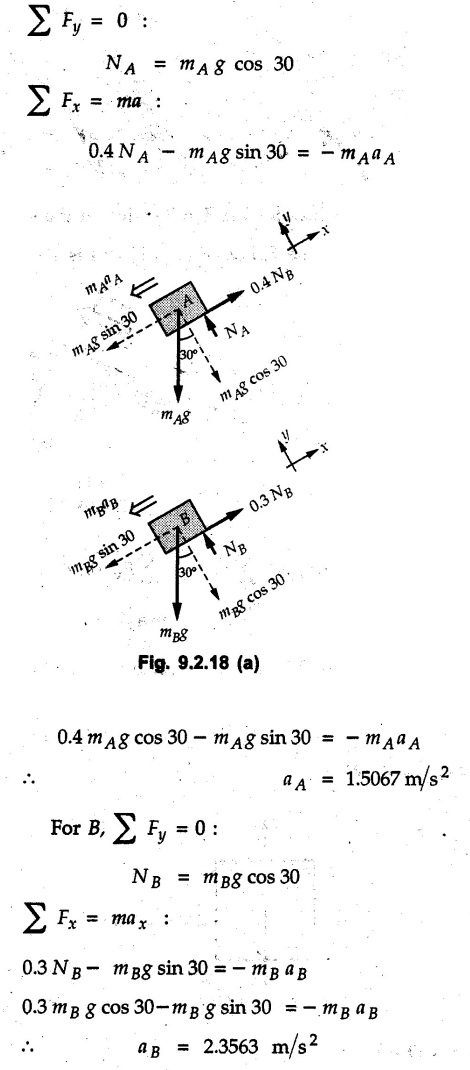
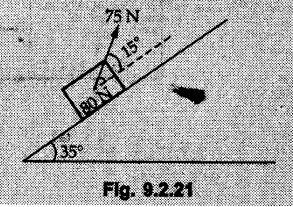
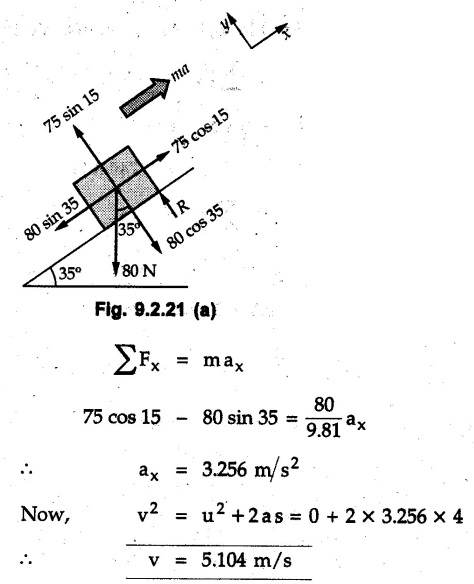
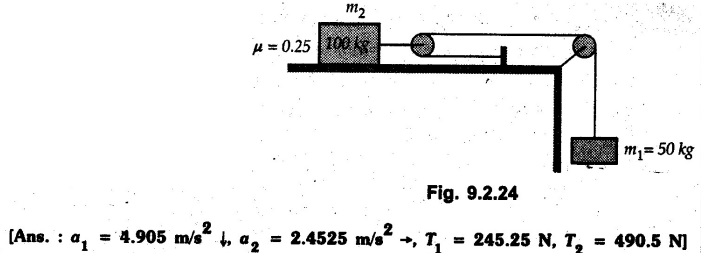
KINETICS - NEWTON'S SECOND LAW OF MOTION • Kinetics is the study of motion of bodies by considering the forces acting on them. In rectilinear motion, acceleration is caused by unbalanced force. • Newton's second law is used to find acceleration of bodies which are treated as particles. Once acceleration of the body is known, the methods discussed in section 9.1 are used for further analysis. • Newton's second law of motion can be stated as follows: • The acceleration of a particle is directly proportional to magnitude of the resultant force acting on it and is in the direction of resultant force. • Mathematically, it can be written as, Where, m is the mass of the particle. The above equation in two dimensions can be written in scalar form as • This equation indicates that if a vector – • The vector - • We can say that the particle is in a state of dynamic equilibrium. This is called D'Alembert's principle of dynamic equilibrium. • The inertia vector is a measure of the opposition that is offered by an object when we try to change its state of rest or of uniform motion along a straight line. • Problems can be solved using either Newton's second law as expressed by equation (9.2.1) or D'Alembert's principle equation (9.2.4). • However, we will use Newton's second law throughout this chapter. The inertia force will be used for pseudo forces which are experienced by objects when kept inside/on other accelerated objects. • For example, if a bus accelerates forward, a man inside the bus experiences a force in the backward direction. This force experienced by the man is a product of mass of man and acceleration of bus and acts in a direction opposite to the direction of acceleration of the bus. We will use the term 'inertia force' to represent such forces. • Problems on kinetics of particles in rectilinear motion can be classified broadly into the following types: 1) Variable force: When atleast one of the forces acting on the particle is variable, the acceleration will be variable. Methods discussed for variable acceleration in Chapter 10 then have to be used for further analysis. 2) Constant forces: If all forces acting on the object are constant, the acceleration will be constant. For further analysis we have to use kinematical equations 3) Dependent motion: If objects are connected by cords/cables then the accelerations of such objects are related. Equations relating accelerations of connected objects can be obtained using methods discussed in section 9.1.5. The tensile tes are related using the equilibrium of pulleys and the concept that tensile force throughout a given string is constant in absence of friction. Pulleys can be considered to be equilibrium eventhough they may be accelerated as their mass will be considered negligible. Hence, 4) Relative motion: When an object is kept inside/on another object, the acceleration of the first object can be obtained with respect to the second. Then, knowing the absolute acceleration of the second object, the absolute acceleration of the first object can be obtained. General Procedure for Solving Problems 1) Draw free body diagram of the objects in statics. The additional term now that has to be shown is the 2) Choose co-ordinate axes parallel and perpendicular to the direction in which motion can take place. For example, if an object is moving on an inclined plane, choose x-axis parallel to inclined plane and y-axis perpendicular to it. 3) Use to find acceleration of the object. 4) If objects are connected through cables, relate their acceleration and tensile forces in connecting cables. 5) Take Example 9.2.1 A rigid body is acted upon by a force of 100 N, the velocity of body changes from 15 m/s to 25 m/s during a period of 50 s. Find the mass of body and the distance moved by the body during the time interval. Solution : Example 9.2.2 A body of mass 5 kg accelerates at a constant rate of 2m/s2 on a smooth horizontal surface due to external force acting at 30° with the horizontal. Find the magnitude of the force. Solution: As the force is át 30° to horizontal, the component of force causing acceleration is F cos 30. Example 9.2.3 A 2000 kg automobile is driven down a 5° inclined plane at a speed of 100 km/h when the brakes are applied causing a constant total breaking force (applied by the road on the tires) of 7 kN. Determine the distance travelled by the automobile as it comes to a stop. Solution: The F.B.D. of automobile is shown in Fig. 9.2.1. Example 9.2.4 Block P of weight 100 N and block Q of weight 50 N are connected by a rope that passes over a smooth pulley as shown in Fig. 9.2.2. Find the acceleration of the blocks and the tension in the rope, when the system is released from rest. Neglect the mass of the pulley. Solution: Let T = Tension in the rope. If P has a downward acceleration a, Q will have upward acceleration a. The free body diagrams of P and Q are shown in Fig. 9.2.2 (a). P moves down and Q moves up, both with the same magnitude of acceleration 3.27 m/s2. Example 9.2.5 A body of mass m sinks slowly in a liquid. The resistance to the motion is F = kv where v is the speed of the body and k is a constant. If the body starts from rest, show that the distance s it sinks in time t is Solution: The F.B.D. of the body is shown in Fig. 9.2.3. Example 9.2.6 At the instant of touchdown, a 7000 kg jet aircraft has its braking parachute deployed and power shut off. If the total drag force on the aircraft varies as FD =20v2 where Fp is the drag force in N and v is the aircraft speed in m/s, calculate the distance x along the runway to reduce the touchdown speed by 50 %. Solution: As the drag force is opposite to the direction of motion, Example 9.2.7 The 50 kg crate is projected along the floor with an initial speed of 7 m/s at x = 0. The coefficient of kinetic friction μk = 0.4. Calculate the time required for the crate to come to rest and corresponding distance x travelled. Refer Fig. 9.2.4. Solution: The F.B.D of crate is shown in Fig. 9.2.4 (a). N1 - 50 × 9.81 = 0 ⸫ N1 = 490.5 N Example 9.2.8 A man moves a box by pushing horizontally against it until it slides on the floor. If μs = 0.4 and μk = 0.35, determine the acceleration with which the crate begins to move. Assume that the force exerted by the man at impending motion is maintained when sliding begins. Solution: Let m = Mass of the box. The limiting value of applied force P to move the box is obtained by using limiting static friction force in the F.B.D. as shown in Fig. 9.2.5 (a). When object starts moving, the frictional force is μkN as shown in Fig. 9.2.5 (b). The effect is ma. Example 9.2.9 A body of mass 'm' is projected up a 25° inclined plane with an initial velocity of 15 m/s. If the coefficient of friction μk = 0.25, determine how far the body will move up the plane and the time required to reach the highest point. Solution: From Fig. 9.2.6, Example 9.2.10 The coefficient of friction between blocks A and C and the horizontal surfaces are μs = 0.24 and μk = 0.20. If mA = 5 kg, mB = 10 kg and mC = 10 kg, determine. i) The tension in the cord. ii) The acceleration of each block. Refer Fig. 9.2.7. Solution : Choose xA, xB and xC as shown in Fig. 9.2.7 (a). Let aA and aC be towards the origin i.e., towards the centre, then aB will be away from origin i.e., downwards. The tensile forces are shown in Fig. 9.2.7 (a). The free body diagrams of A, B and C are shown in Fig. 9.2.7 (b). From equations (1), (2) and (3), Example 9.2.11 The system shown in Fig. 9.2.8 is initially at rest. Neglecting friction, determine i) The force P required if the velocity of the collar B is to be 5 m/s after 2 seconds. ii) The corresponding tension in the cable. Solution : Taking the fixed pulley as origin and defining distance upto A and B as xA and xB respectively, 5 = 0 + a (2) a = 2.5 m/s2 The two free body diagrams are shown in Fig. 9.2.8 (a). Example 9.2.12 A hockey player hits a puck so that it comes to rest in 9 s after sliding 30 m horizontally on the ice. Determine a) The initial velocity of the puck, b) The coefficient of friction between the puck and ice. Solution : t = 9 s, s = 30 m, v = 0 v = u + at : From equation. (1), u = - 9 a Substituting in equation (2), Consider F.B.D. of the puck shown in Fig. 9.2.9. Example 9.2.13 How much is the driving force needed to pull a train weighing 3200 kN from rest to a speed of 24 kmph in 20 seconds if the coefficient of rolling friction is 0.02 and if, 1) The track is horizontal ii) The track is inclined upwards at an angle of 10%, with the horizontal, Solution: When track is inclined at 10° the F.B.D. will be as shown in Fig. 9.2.10 (b). Example 9.2.14 Block A of mass 100 kg and block B of mass 300 kg are competed by a light string arranged as shown in Fig. 9.2.11. The two blocks start from rest. The horizontal plane and the pulley are frictionless and mass of the movable pulley is negligible. Calculate the tension in the string and the acceleration of each block. Solution: From Fig. 9.2.11 (a), The free body diagrams of the two objects are shown in Fig. 9.2.11 (b). From equation (1) and (2), Example 9.2.15 The conveyor belt as shown in Fig. 9.2.12 is designed to transport packages of various weights. Each 10 kg package has a coefficient of friction μx = 0.15. If the speed of the conveyor is 5 m/s, and then it suddenly stops, determine the required time and distance the package will slide on the conveyor before coming to rest. Solution: Consider that the package is moving towards right. When conveyor stops, package starts moving with velocity 5 m/s towards right due to inertia. Consider F.B.D. of package shown in Fig. 9.2.12 (a). Example 9.2.16 A elevator being lowered into a mine-shaft starts from rest and attains a speed of 10 m/s within a distance of 15 meters. The elevator alone has a mass of 500 kg and it carries a box of mass 600 kg in it. Find the total tension in the cables supporting the elevator, during this accelerated motion. Also find the total pressure between the box and the floor of the elevator. Solution: For the elevator, u = 0, v = 10 m/s, S = 15 m v2 = u2 + 2as : 102 = 0 + 2a (15) a = 100 / 30 = 33.333 m/s2 The F.B.D. of elevator carrying the box is shown in Fig 9.2.13 (a). The total pressure between the box and the floor can be obtained from the F.B.D of box shown in Fig. 9.2.13 (b). 600 a is inertia force directed opposite to acceleration of lift. Acceleration of box with respect to lift is zero. Example 9.2.17 Two masses are connected by a string as shown in Fig. 9.2.14. Neglecting inertia and friction of both pulleys calculate acceleration a1 of 150 kg block when system is released from rest. If a force of (200×9.81)N is applied in place of 200 kg block what would be acceleration of 150 kg ? Comment on the results. Solution: Let acceleration of 200 kg block be a1↓. Then acceleration of 100 kg block will be a1↑. Let T = Tension in string. The free body diagrams of the two blocks are shown in Fig. 9.2.14 (a). From equations (1) and (2), T = 1681.8 N If a force of 200 × 9.81 is applied instead of 200 kg block, the tensile force is T = 200 × 9.81 ⸫ 200 × 9.81 - 150 × 9.81 = 150 a1 When block is attached, tension is less than the weight due to inertia of the block. Hence if a force of 200 × 9.81 is applied instead of block B, we get more acceleration. Example 9.2.18 Determine the minimum stopping distance 's' and the corresponding time 't’ required by a truck, if a crate kept on the horizontal flat bed of the truck is not to slip forward. Take μs = 0.4 and μk = 0.3 between the crate and the flat bed of the truck which has a speed of 90 km/h. Solution: Assuming that the truck is moving to the right and brakes are applied causing deceleration of magnitude 'a', the crate will be subjected to inertia force ma to the right as shown in Fig. 9.2.15. If the crate does not move on the truck, its acceleration with respect to the truck is zero." Example 9.2.19 Determine the apparent weight of a 70 kg man in an elevator when the acceleration of elevator is a) Zero, b) 2 m/s2 upwards and c) 2 m/s2 downwards. Solution: Apparent weight is the normal reaction. When acceleration of elevator is zero, there is no inertia force due to motion of elevator on the man. The F.B.D. is shown in Fig. 9.2.16 (a). When lift accelerates upwards, the inertia force ma is downwards as shown in Fig. 9.2.16 (b). When lift accelerates downwards, the inertia force ma is upwards as shown in Fig. 9.2.16 (c). Example 9.2.20 For what values of angle θ will the acceleration of the 3 kg block be 6 m/s2 to the right when subjected to a 30 N as shown in Fig. 9.2.17. Take μs = 0.6 and μk = 0.5 between the block and the floor Solution : For F.B.D. of block shown in Fig. 9.2.17 (a). Squaring we get, 900 cos2θ = 1070.27 + 225 sin2 θ - 981.45 sin θ 900 (1- sin2 θ) = 1070.27 + 225 sin2 θ ́- 981.45 sin θ 1125 sin2 θ - 981.45 sin θ + 170.27 = 0 sin θ = 0.6335 or 0.239 Example 9.2.21 Two blocks A and B are held stationary 10 m apart on a 30° incline as shown in Fig. 9.2.18. If the blocks are released simultaneously, calculate the time taken and distance travelled by each block just before collision. Solution: For F.B.D. of A shown in Fig. 9.2.18 (a). When A and B collide Dividing equation (1) by (2), Example 9.2.22 A block and pulley system is shown in Fig. 9.2.19. The coefficient of kinetic friction between the block and the plane is 0.25. The pulley is frictionless. Find the acceleration of the blocks and the tension in the string when the system is just released. Also find the time required for 100 kg block to come down by 2 m. Solution: Let T = Tension in the string The F.B.D. of both blocks is shown in Fig. 9.2.19 (a). Solving equations (ii) and (iii), For 100 kg block to come down 2 m, Example 9.2.23 Two blocks 'A' and 'B' of masses mA 280 kg and mg = 420 kg are joined by an inextensible cable as shown in Fig. 9.2.20. Assume that the pulley is frictionless and μ = 0.30 between block 'A' and the surface. The system is initially at rest. Determine (i) Acceleration of block A (ii) Velocity after it has moved 3.5 m and (iii) Velocity after 1.5 seconds. Solution: Since both the blocks are connected by single rope, acceleration of both the blocks will be same. For block A, As per Newton's 2nd law of motion, For block B, Velocity of block A after if has moved 3.5 m Velocity of block A after 1.5 seconds is, Example 9.2.24 An object weighing 80 N is pulled up on the smooth plane by a 75 N force as shown in Fig. 9.2.21. Determine the velocity of the object after it has moved 4 m. Solution: As per Newton's second law of motion, Example 9.2.25 Two blocks are joined by an inextensible cable as shown in Fig. 9.2.22. If the system is released from rest, determine the velocity of block A after it has moved 2 m. Assume that the coefficient of kinetic friction between block A and the plane is μk = 0.25 and that the pulley is weightless and frictionless. Solution: When A moves 2 m to the right, B moves 2 m downward. Both have the same speed. By work-energy principle, Examples for Practice Q.1 Masses A and B of 30 kg each are connected by a light inextensible rope passing over a smooth light pulley as shown in Fig. 9.2.23. Mass A slides over a smooth inclined plane making an angle of 30° with the horizontal. If the system is released from rest, find the distance moved by mass B in 2 seconds. [Ans. : 4.905 m] Q.2 Two blocks shown in Fig. 9.2.24 start from rest. If = 0.25 100 kg the chord is inextensible, friction and inertia of pulley are negligible, calculate acceleration of each block and tension in each chord. Q.3 A particle having rectilinear motion has 16 kg mass and is acted upon by a force F = 30t2+e-t newtons, where 't' is time in seconds. If particle has initial velocity 3 m/s, find position and velocity at t = 2 s. [Ans. : 8.625 m, 8.054 m/s]Kinetics: Force and Acceleration
Newton's Second Law of Motion


![]() is added to the forces acting on the particle, we get an equation that resembles equilibrium.
is added to the forces acting on the particle, we get an equation that resembles equilibrium.![]() , which has same magnitude as
, which has same magnitude as ![]() but opposite direction, is called the inertia vector.
but opposite direction, is called the inertia vector.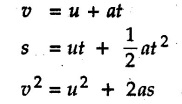
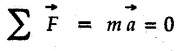
![]() term, which is the effect. To differentiate the effect from the causes, we will show the effect with a double arrow (→)
term, which is the effect. To differentiate the effect from the causes, we will show the effect with a double arrow (→)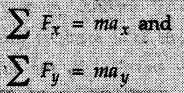
![]() term in the direction of motion so that if 'a' comes out to be negative it will indicate deceleration.
term in the direction of motion so that if 'a' comes out to be negative it will indicate deceleration.Solved Examples for Understanding





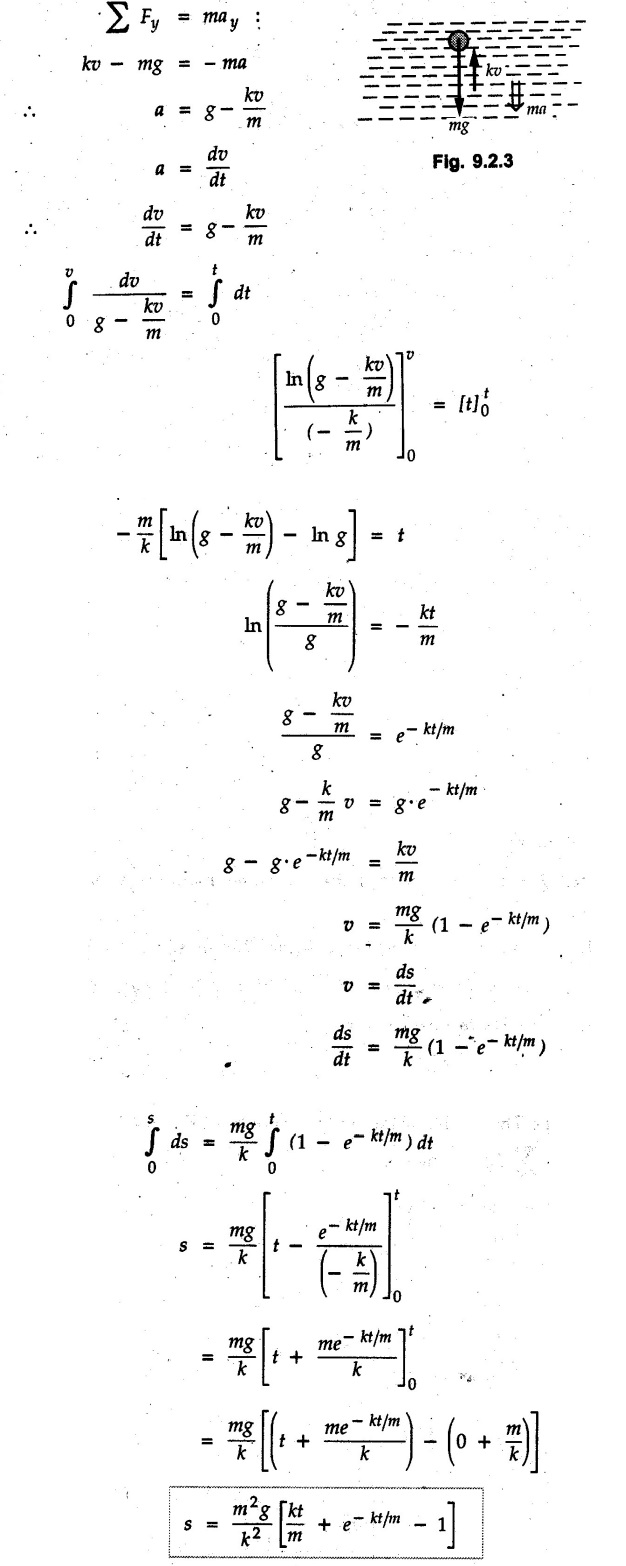
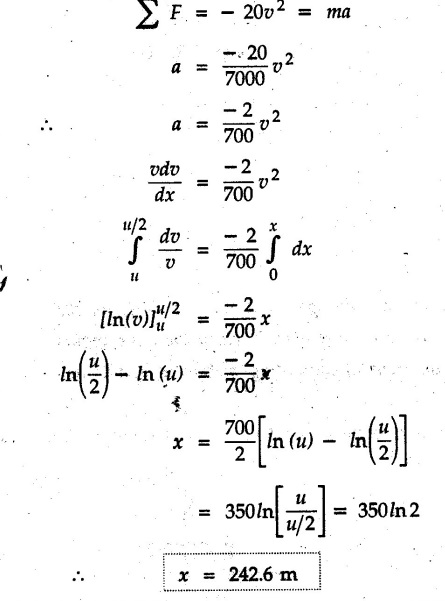

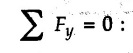


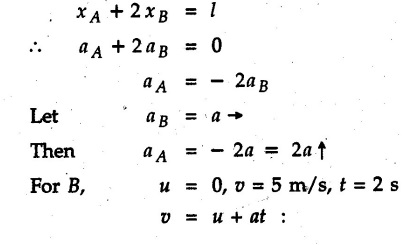


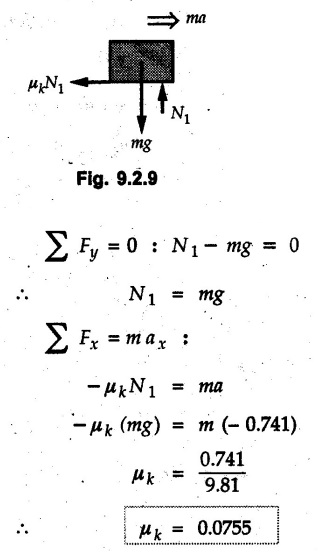











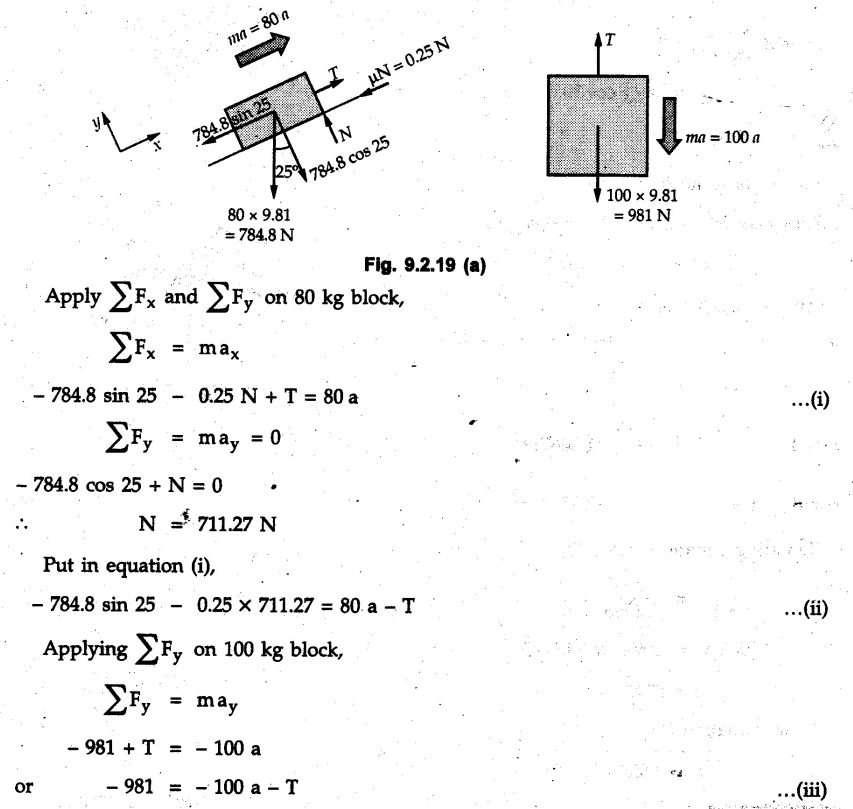
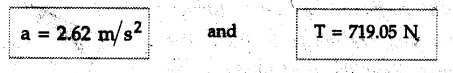





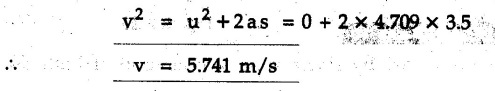
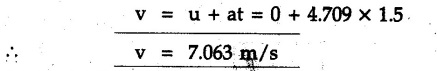


Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : with Solved Example Problems - Kinetics - Newton's second law of Motion
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
