Engineering Mechanics: Unit V: Dynamics of Particles
Kinetics - Energy and Momentum Methods
with Solved Example Problems
One method to solve problems involving motion of particles is to make use of Newton's second law to determine acceleration and then use principles of kinematics to determine velocity and position at any time.
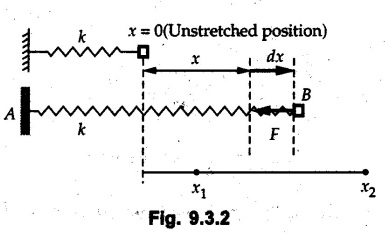
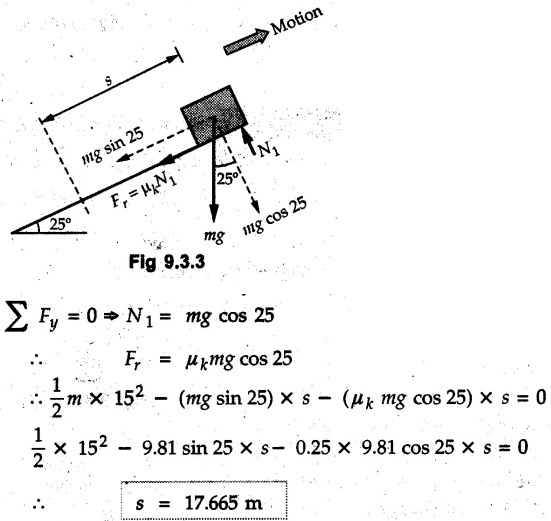
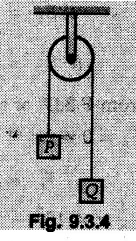
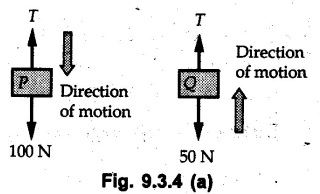
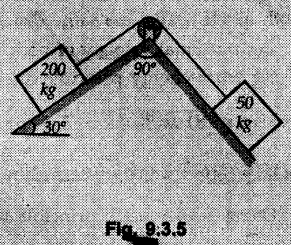
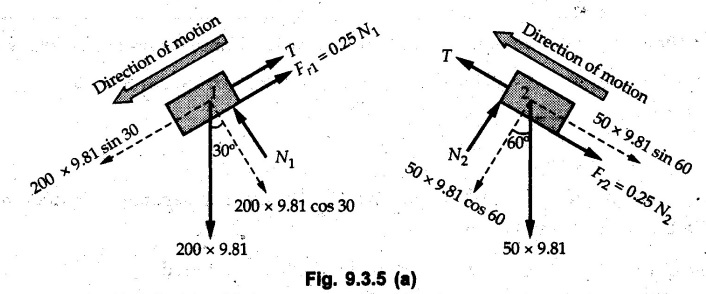
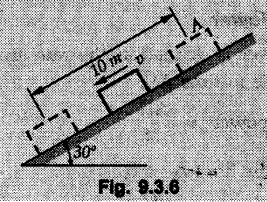
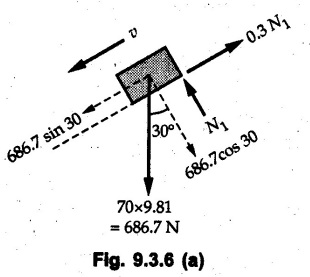
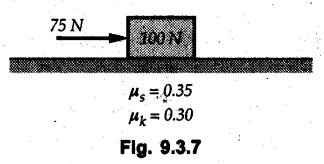
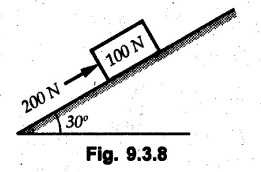
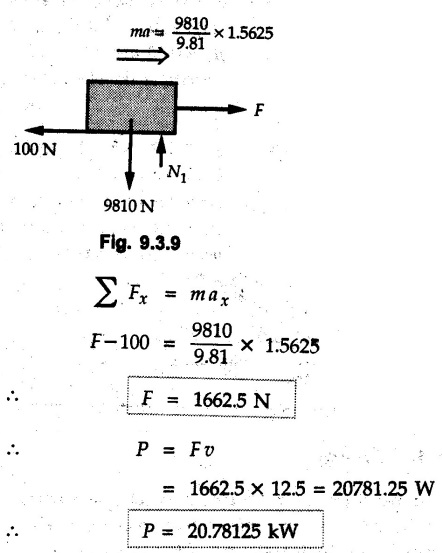
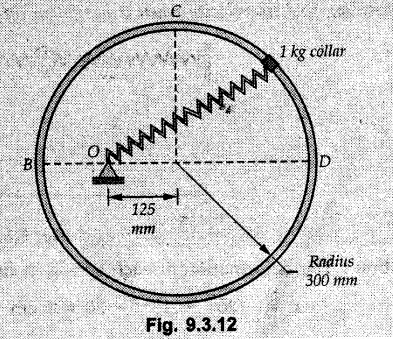
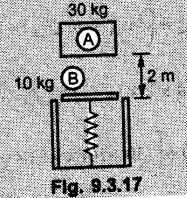
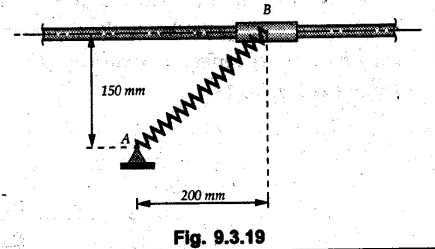
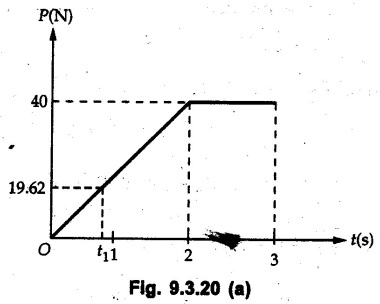
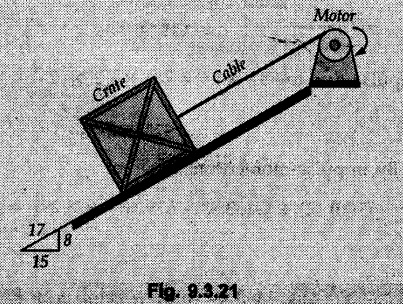
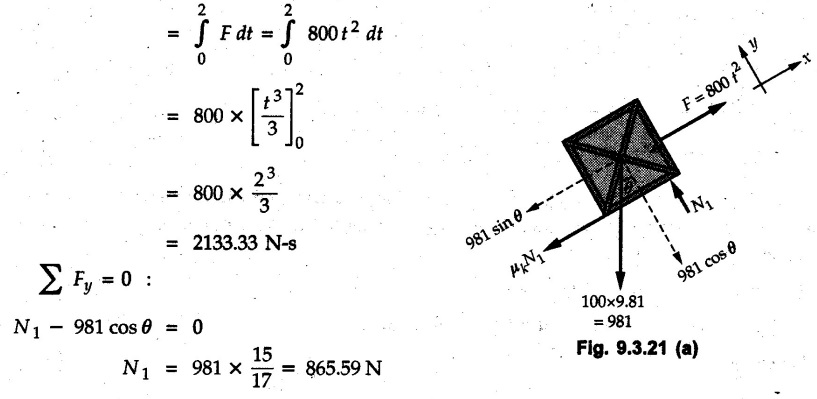
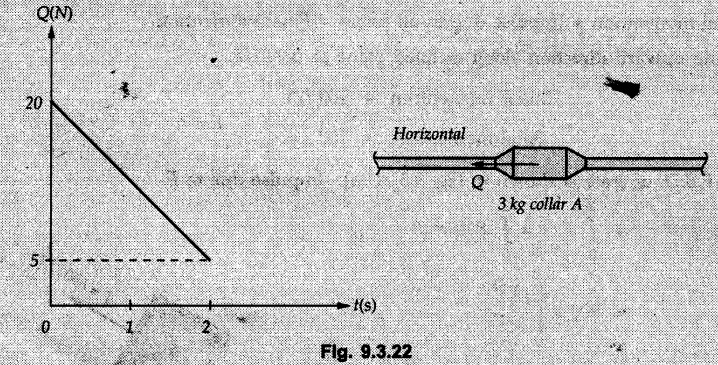
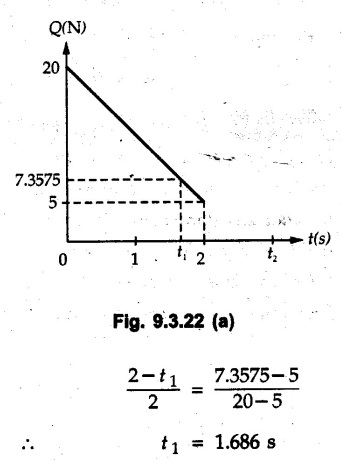
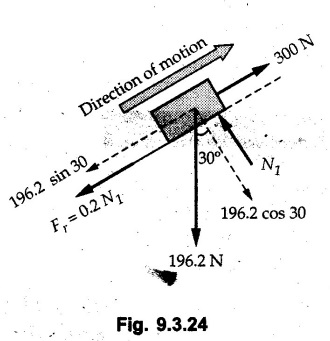
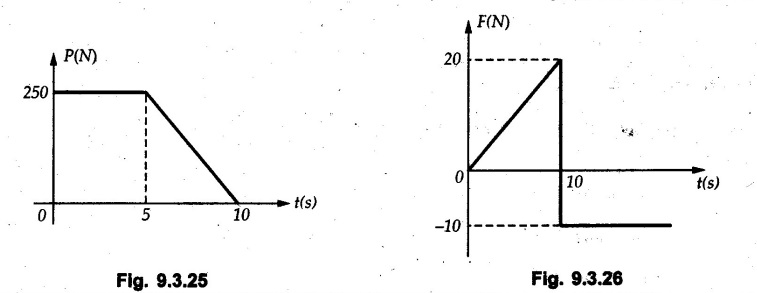
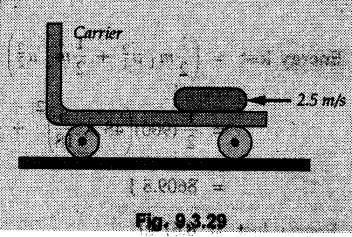
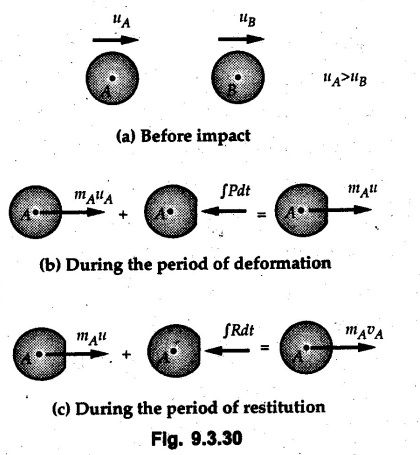
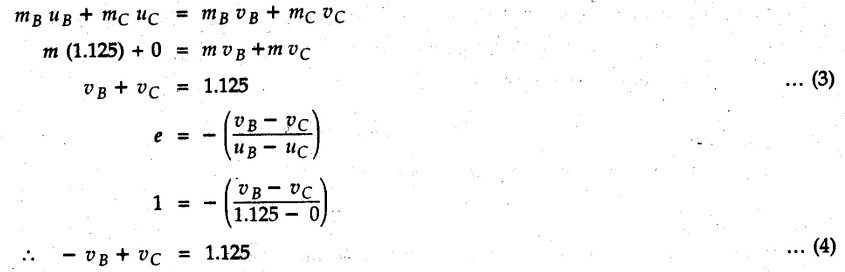
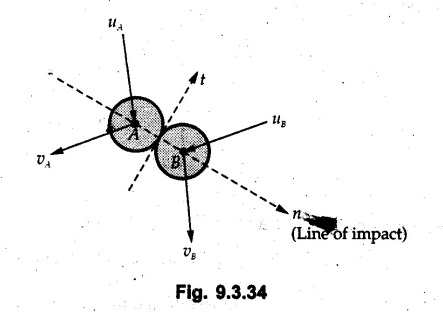
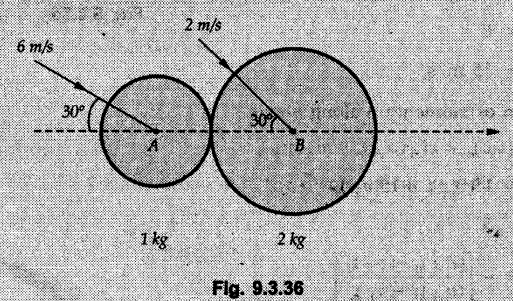
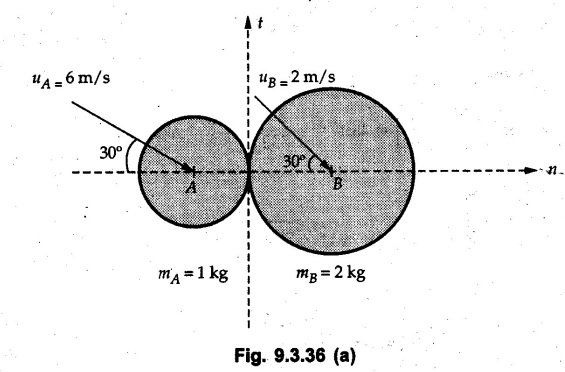
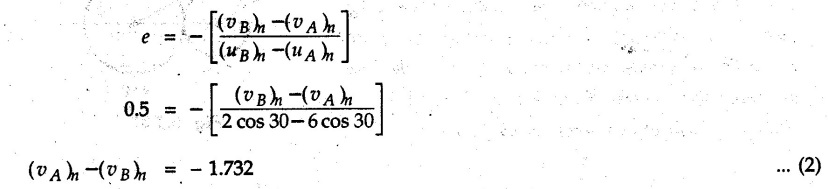
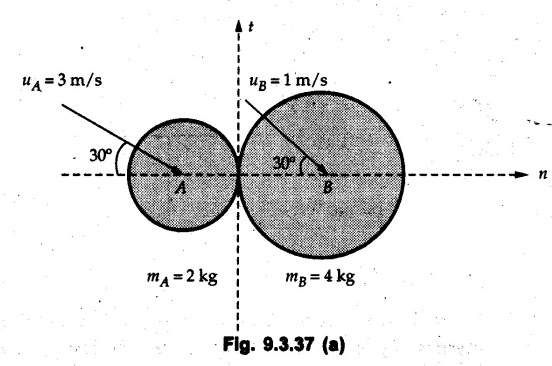
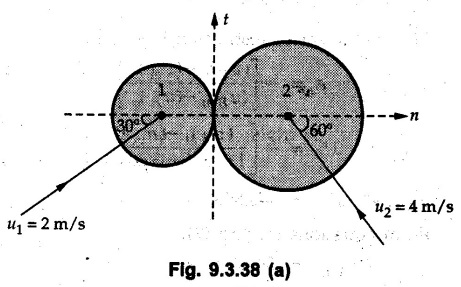
KINETICS - ENERGY AND MOMENTUM METHODS • One method to solve problems involving motion of particles is to make use of Newton's second law to determine acceleration and then use principles of kinematics to determine velocity and position at any time. • Two additional methods will be discussed in this chapter the method of 'work and energy', and the method of 'impulse and momentum', which do not require the determination of acceleration. • The method of work and energy directly relates force, mass, velocity and displacement. The method of impulse and momentum relates force, mass, velocity and time. 1. Work of a Force • If a force where • If a graph of F cos versus s is given, the R.H.S represents area under the graph. If the magnitude of force is constant and acts at a constant angle θ with the direction of displacement, • The work done by a force is positive when the component of force parallel to displacement (i.e. F cos θ) is in the direction of displacement. When they are in opposite directions, the work done is negative. The unit of work is joule (J). • Work done by weight : If dy is the upward displacement of an object of weight w, du = -w dy Negative sign is due to opposite directions of w and dy. • If object moves downwards, Ay will be negative and the work done will be positive. Work Done by Spring Force : • Consider a block B connected to a spring as shown in Fig. 9.3.2. The spring is undeformed when block is at position x = 0. • When the block is taken from x to x + dx, the work done is dU = - F dx [F and dx are in opposite direction] As F = kx in magnitude, ⸫ dU = – kx dx • If the block is taken from x = x1 to x = x2, the work done is • While using the above equation, mistakes in sign can be eliminated by calculating the magnitude of work done using • Of particular interest, is a special case when either x1 or x2 is zero. Then the magnitude of work done is where x represents either elongation or compression of the spring, i.e., deformation. • This work done on the spring is stored in it as potential energy called the spring potential energy. 2. Principle of Work and Energy • Consider a particle of mass m subjected to a single force F. Then, • The quantity 1/2 mv2 is defined as the kinetic energy of particle. Its S.I unit is joule(J). The above equation represents the work-energy principle. General Procedure for Solving Problems 1) Draw F.B.D. of the object. ii) Resolve all forces into two mutually perpendicular directions - parallel and perpendicular to displacement. iii) Identify velocities at initial position 1 and final position 2 to write KE1, and KE2. iv) Calculate U1-2, ie, the work done by all forces parallel to the direction of displacement. If force is in the direction of displacement then the work done will be positive. If force is in a direction opposite to displacement, work done is negative. Work done by forces perpendicular to displacement is zero. v) Use the work-energy principle to find required quantities. Note: The work energy principle cannot be used to find acceleration or forces for which the work done is zero. Solved Examples for Understanding Example 9.3.1 A body of mass 'm' is projected up 25° inclined plane with initial velocity 15 m/s. If μs = 0.28 and μk = 0.25, determine how far the body will move up the plane and time required to reach the highest point. Solution: Let s = Distance travelled up the plane. By work-energy principle, K.E1 + Work done by all forces = K.E2 From F.B.D. of the body shown in Fig. 9.3.3. Distance = (Average velocity) × Time Example 9.3.2 A 1/8 kg bullet travelling at 150 m/sec. will penetrate 125 mit into a fixed block of wood. Find the velocity with which it would emerge if fired through a fixed board 60 mm thick. The resistance being supposed to be uniform and to have same value in each case. Solution: Let R be the resistance force. By work energy principle, K.E1 + Work done by all forces = K.E2 The work done is negative as R acts opposite to displacement. K.E2 = 0 ⸫ 1406.25 - R (0.125) = 0 ⸫ R = 11250 N For the board, let v be the velocity with which bullet emerges Example 9.3.3 Block P of weight 100 N and Q of weight 50 N are connected by a cord that passes over a smooth pulley as shown in Fig. 9.3.4. Find the velocity of the blocks after they have moved 2 m starting from rest and the tension in the cord. Use work-energy principle. Solution: The free body diagrams with the directions of motion are shown in Fig. 9.3.4(a): Both blocks travel the same distance and move with the same speed. Using work-energy principle for P, Adding equation (1) and (2), Example 9.3.4 A block and pulley system is shown in Fig. 9.3.5. The pulley is frictionless. Find the tension in the cable and the velocity of 50 kg block after it has moved a distance of 1.5 m when the system starts from rest. Neglect the mass of the pulley. Take the coefficient of kinetic friction between the blocks and the planes as 0.25. use the principle of work and energy. Solution: • To use principle of work and energy, draw free body diagrams of the two blocks and resolve all forces parallel and perpendicular to the direction of motion as shown in Fig. 9.3.5 (a). • The work done by forces acting perpendicular to the displacement is zero. For forces acting parallel to the displacement, work done is product of force and displacement. if the force is in the direction of displacement, work done is positive. • If the force is opposite to direction of displacement, work done is negative. For 200 kg block, N1 = 200 × 9.81 cos 30 ⸫ Fr1 = 0.25× 200 × 9.81 cos 30 For 50 kg block, N2 = 50 × 9.81 cos 60 ⸫ Fr2 = 0.25 × 50 × 9.81 cos 60 • By work-energy principle, Initial kinetic energy + Work done by all forces = Final kinetic energy For both blocks, initial velocity is zero. Hence their initial kinetic energy is zero. Both blocks travel the same distance of 1.5 m. • Let v = Final velocity of both blocks. Using work-energy principle for 200 kg block, • Using work-energy principle for 50 kg block, Note: The velocity can be obtained by considering the complete system as follows: 0 + [200 × 9.81 × sin 30 × 1.5 - 50 × 9.81 × sin 60 × 1.5 - 0.25 × 200 × 9.81 cos 30 × 1.5 -0.25 × 50 × 9.81 cos 60 × 1.5] = 1/2 × 250v2 ⸫ v = 0.9173 m/s As T is an internal force when the two objects are not separated, it does not appear in the work-energy equation. To find T, free body diagram of one of the blocks has to be used. Example 9.3.5 If a 70 kg block shown in the Fig. 9.3.6 is released from rest at A. Determine its speed after it slides 10 m down the plane. Take the coefficient of friction as 0.3. Solution: The speed of the block can be obtained using work energy principle. The forces acting on the block parallel to velocity are shown in Fig. 9.3.6 (a). N1 = 686.7 cos 30 Using work-energy principle, Initial K.E. + Work done by all forces = Final K.E. 0 + (686.7 sin 30 × 10− 0.3× 686.7 cos 30 × 10) Examples for Practice Q.1 A block of mass 'm' is projected down a 30° incline with a velocity of 1 m/s. If μs = 0.35 and μk = 0.30, determine the velocity of the block after it has travelled a distance of 2 m along the inclined plane. [Ans. : 3.23 m/s] Q.2 A horizontal force of 75 N is applied to a 100 N block lying on a horizontal surface as shown in Fig. 9.3.7. If μs = 0.35 and μk = 0.30, determine the velocity of the block after it has travelled 5 m. [Ans. : 6.644 m/s] Q.3 A 200 N force is applied to a 100 N block as shown in Fig. 9.3.8. The block is initially at rest. If μs = 0.3 and μk = 0.2, determine the velocity of the block after it has travelled 3 m up the 30° incline. [Ans. : 8.837 m/s] 3. Power • Power is defined as the rate at which work is done. If AU is the amount of work done in time Δt, The S.I. unit of power is watt (W). Power can be calculated using either equation (9.3.6) or (9.3.7). Solved Examples for Understanding Example 9.3.6 A car of weight 9810 N accelerates from rest to a speed of 45 km/hr in a distance of 50 m against a resistance of 100 N. Find the average driving force acting on the car. Using the average force, find the greatest power developed by the engine. Solution : u = 0, v = 45 km/h = 12.5 m/s s = 50 m v2 = u2 + 2 as 12.52 = 0 + 2a × 50 a = 1.5625 m/s2 The F.B.D. of car is shown in Fig. 9.3.9. Example 9.3.7 A train of mass 400 tonnes acquires a speed of 72 km/h in a distance of 5 km from start, when travelling up an incline of 1 in 200. If the frictional resistance is 200 N per tonne mass, determine the tractive force exerted by the engine during the operation and the power developed when the speed was 54 km/h. Solution: u = 0, v = 72 km/h = 20 m/s s = 5 km = 5000 m v2 = u2 + 2 as 202 = 0 + 2a (5000) ⸫ a = 0.04 m/s2 The F.B.D. of train is shown in Fig. 9.3.10. Examples for Practice Q.1 A train weighing 4000 kN is driven by an engine on a level track at constant speed of 54 km/h. Resistance due to friction is 5 N per kN weight of the train. Find the power of the engine. [Ans. : 300 kW] Q.2 Find the power when a 70 kg man riding a 15 kg bicycle travels up a 10° incline. [Ans.: 724 W] 4. Conservative Forces and Potential Energy • If the work done by a force does not depend on the path along which the particle is taken from one point to another, the force is called conservative force. In such a case the work done depends on the initial and final positions of the particle. • For example, the work done by weight (U1-2 = -W Δy) depends only on the difference of height Δy. • Even if the object is taken from A to B along different paths ACB, AEB or ADB, the work done remains same. Similarly, the work done by spring force • Friction is a non-conservative force. The work done by friction depends on the path. • Potential energy of a particle is due to the position of the DC particle (Kinetic energy is due to velocity). • It is defined for the conservative forces for which the work done depends only on the initial and final position like the gravitational force and the spring force. • In mechanics we come across two types of potential energies the gravitational potential energy and the potential energy in a spring (the spring potential energy). Gravitational Potential Energy (G.P.E) : • G.P.E. = mgh = Wh where h is measured from a reference level. Although, any reference level can be taken, it is more convenient to take lower of the two positions as reference so that gravitational potential energy at the lower position becomes zero. Spring Potential Energy (S.P.E) where k = Spring constant and x = Deformation of spring. 5. Conservation of Energy • Principle of conservation of energy states that under the action of only conservative forces, the sum of kinetic energy and potential energy of a particle remains constant. • If a particle under the action of only conservative forces is taken from position 1 to position 2, • Conservation of energy implies that during the motion of particle, the kinetic energy will be converted to potential energy or potential energy to kinetic energy so as to keep the total energy constant. • An important result which can be remembered while solving problems is the velocity attained by an object falling freely under gravity through height 'h', starting from a state of rest. Its potential energy gets converted to kinetic energy. Example 9.3.8 A particle of mass 10 kg falls vertically from a height of 100 m from ground. What is the change in potential energy when it has reached a height of 50 m ? Solution: The change in height is h = 50 m. Change in potential energy = mgh = 10 × 9.81 × 50 = 4905 J ⸫ The potential energy decreases by 4095 J. Example 9.3.9 A 1 kg collar is attached to a spring of stiffness 250 N/m and can slide freely without friction on a circular rod in horizontal plane. Spring is undeformed when collar is at B. Knowing that collar passes through point D with speed 1.8 m/s, determine velocity of collar as it passes through point C and point B. Solution: As the rod is in horizontal plane, there is no change in height Undeformed length of collar = OB = 300 – 125 = 175 mm. Deformation of spring at B = xB = 0 At D, xD = (300 + 125) - 175 = 250 mm. ⸫ xC = 150 mm Using conservation of energy for D and C, Using conservation of energy for D and B, Example 9.3.10 Two springs of stiffness 0.5 N/cm and unstretched length 20 cm each are connected to sphere B of 5 kg mass shown in Fig. 9.3.13. If released from rest from this position, find its velocity when it has fallen through 15 cm. Solution: The deformation of each spring in final position is, By conservation of energy, K.E1 + G.P.E1 + S.P.E1 = K.E2 + G.P.E2 + S.P.E2. Taking the lower position as reference, the height of initial position is 15 cm. Example 9.3.11 A 8 kg plunger is released from 600 mm height onto nested springs. Outer and inner springs have constants 4 kN/m and 12 kN/m respectively. Calculate maximum deformation of outer spring. Solution: If outer spring is compressed by 'x', inner spring will be compressed by (x − 0.09). By conservation of energy, K.E1 + G.P.E1 + S.P.E1 = K.E2 + G.P.E2 + S.P.E2. Taking the final position as reference, the height of initial point is h = (x + 0.6), The other value of x is 1.317 × 10-3m = 1.317 mm for this value of x, x - 0.09 = -0.089 m which would mean that the inner spring will be elongated. This is not possible when the plunger is falling. Example 9.3.12 The double spring bumper is used to stop the 7500 N steel billet in a rolling mill. Determine the stiffness k = k1 = k2 of each spring so that no spring is compressed more than 0.06 m after it is struck by the billet travelling with a speed of 2.4 m/s. Neglect the mass of the springs, rollers and the plates A and B. Refer Fig. 9.3.15 Solution: Both springs will be compressed by 0.06 m in the final position of the billet when it comes to rest. By conservation of energy, Example 9.3.13 A 1.5 kg collar is attached to a spring and slides without friction along a circular rod in a horizontal plane. The spring has an undeformed length of 150 mm and a constant k = 400 N/m. Knowing that the collar is in equilibrium at A and is given a slight push to get moving, determine the velocity of the collar as it passes point B. Refer Fig. 93.16 Solution: By conservation of energy, Example 9.3.14 A 30 kg block dropped from a height of 2 m onto the 10 kg pan of spring scale as shown in the Fig. 9.3.17. Assuming the collision to be perfectly plastic. Determine the maximum deflection (Compression of the pan). The spring constant is k = 20 kN/m. Solution: Applying principle of conservation of energy between 1 and 2 (on block A) • For perfectly plastic impact, velocity after impact is same • Initial spring deflection due to pan weight is, • Again applying principle of conservation of energy between 3 and 4, Example 9.3.15 A package of mass 60 kg, moving with velocity 2.5 m/s on a surface of friction μ hits a spring of constant 20 kN/m and compressed initially by 12.0 cm. If block compresses the spring further to the maximum of 4.0 cm and the block is initially 60 cm away from end of spring, determine μy and velocity of block when it just starts pressing spring (see Fig. 9.3.18). Solution: Given: m = 60 kg, v1 = 2.5 m/s, k = 20 kN/m = 20 × 103 N/m, x1 = 12 cm = 0.12 m, x2 = 12 + 4 = 16 cm = 0.16 m, s = 60 + 4 = 64 cm = 0.64 m After compression the package comes to rest, hence v2 = 0. By conservation of energy, Examples for Practice Q.1 A truck of mass 15 tons travelling at 1.6 m/s impacts a buffer spring of spring constant 800 N/mm. Find the maximum compression of the buffer spring. [Ans. : 21.9 cm] Q.2 A 10 kg block is dropped from a height of 2 m on a spring of stiffness 4 kN/m. Determine the maximum compression of the spring. [Ans. : 0.339 m] Q.3 Spring AB of stiffness 2500 N/m is attached to a 3 kg collar which can move freely on a horizontal bar as shown. If unstretched length of spring is 100 mm, determine maximum velocity attained by collar when released from rest from position B. [Ans. : 4.082 m/s] PRINCIPLE OF IMPULSE AND MOMENTUM 6. Impulse and Momentum • From Newton's second law, • The quantity • The above equation is referred to as principle of impulse and momentum or the impulse-momentum theorem. Note that equation (9.3.12) is a vector equation and can be resolved into suitable x and y components. • The impulse can be evaluated in the following ways depending upon nature of force • Impulse momentum theorem must be used only when object is in motion. Example 9.3.16 A 2 kg collar can slide on a frictionless vertical rod and it is acted upon by force P of which magnitude varies as shown in the graph. If collar is initially at rest, find maximum velocity of the collar. Solution: As a graph of force-time is given, we have to use impulse-momentum theorem. The collar moves when P > 2 × 9.81 i.e. P > 19.62 N. Let t1 be the time at which P = 19.62 N as shown in Fig. 9.3.20 (a). By similarity of triangles, The velocity is maximum at t = 3 s as the force P is applied only upto t = 3 s. Hence impulse-momentum theorem is to be used from t = 0.981 s to t = 3 s. The collar is subjected to two forces in vertical direction-upward force P and downward force weight. Upward impulse due to P = Area under the graph from t = 0.981 s to t = 3 s = 70.376 N-s Downward impulse due to weight = mg Δt = (2) (9.81) (3 – 0.981) = 39.613 N-s By impulse momentum theorem, m v1 + Impulse due to all forces = m v2 v1 = 0, v2 = vmax Taking upward quantities positive, 0 + (70.376 - 39.613) = (2) vmax Example 9.3.17 A 100 kg crate is being hoisted up an inclined plane using a motor and cable arrangement as shown. For a short time, force in the cable is F = 800 t2 newtons (where t = time in s). If velocity of create is v1 = 2 m/s at 1= 0, determine velocity at t = 2 s. Assume μs 0.35 and μk = 0.30. Solution: As one of the forces acting on the object is given as a function of 't', we can use impulse-momentum theorem. Initial momentum + Impulse due to all forces = Final momentum. Taking upward direction along inclined plane as positive, Initial momentum = 100 (2) Final momentum = 100 v2 The F.B.D. of crate is shown in Fig. 9.3.21 (a). Impulse due to F Fr = μk N1 = 0.3 × 865.59 ⸫ Fr = 259.68 N Impulse due to friction = Fr · Δt = 259.68 × 2 = 519.36 N-s Impulse due to 981 sin θ = 981 × 8/17 × 2 = 923.29 N-s By impulse-momentum theorem, (100) (2) + [2133.33-519.36 - 923.29] = 100 v2 Example 9.3.18 A 3 kg collar is acted upon by force Q which varies as shown. Collar was initially at rest. Assuming μk = 0.25, find maximum velocity attained by collar and time at which the collar comes to rest. Solution: As force time graph is given, we have to use impulse-momentum theorem. The collar is subjected to two forces-force Q towards left and frictional force Fr = μk mg towards right. Fr = 0.25 × 3 × 9.81 = = 7.3575 N. Maximum velocity is attained when a = 0, i.e., ⸫ Fr = Q, i.e. when Q = 7.3575 N. Let Q = 7.3575 N at time 't1' as shown in Fig. 9.3.22 (a). By similarity of triangles, Impulse towards right due to Fr = μk mg Δt = (0.25) (3) (9.81) (1.686) = 12.4 N-s Impulse towards left due to Q = Area under the graph By impulse-momentum theorem, mv1 + Impulse due to all forces = mv2 0 + [12.4 - 23.062] = 3vmax ⸫ vmax = -3.554 m/s If the block comes to rest at time t2 > 2s, Impulse towards right = μk mg Δt = (0.25) (3) (9.81) (t2) = 7.3575 t2 Impulse towards left = Area under the graph = 25 N-s. v1 = 0, v2 = 0 ⸫ By impulse-momentum theorem 0 + [7.3575t2 - 25] = 0 Example 9.3.19 The force acting on the 250 N crate has a magnitude of F= (12t2) N, where t is in seconds. If the crate starts from rest, determine its speed when t = 5 s. The coefficient of static and kinetic friction between the floor and create are 0.3 and 0.2 respectively, Refer Fig. 9.3.23. Solution: The crate starts moving when F = μs mg ⸫ 12 t2 = 0.3 × 250 ⸫ t = 2.5 s Impulse momentum theorem has to be used from t = 2.5 s to t = 5 s. By impulse-momentum theorem, Initial momentum + Impulse due to all forces = Final momentum In horizontal direction, there are two forces on the block after it starts moving. F acts towards right and μk mg towards left. Initial momentum = 0 as block starts from rest. Let final velocity = v Impulse towards left = μk mg Δt = 0.2 × 250 × 2.5 = 125 N-s Example 9.3.20 A body weighing 196.2 N slides up a 30° inclined plane under the action of an applied force of 300 N acting parallel to the plane. The coefficient of friction is 0.2. The body moves from rest. Determine at the end of the 4 s, the acceleration, distance travelled, velocity, kinetic energy, work done, momentum and impulse applied on the body. Solution: Let a = acceleration of the body To use work-energy principle, draw F.B.D. and resolve forces parallel and perpendicular to the direction of motion as shown in Fig. 9.3.24. By work-energy principle, Examples for Practice Q.1 A 50 kg block resting on a horizontal surface is acted upon by a variable force 'P' which varies as shown in Fig. 9.3.25. If μk = 0.2 between the block and surface, find velocity of block at t = 5s and at t = 10.5. Also find the time when the block will come to rest. [Ans. : 15.19 m/s, 17.88 m/s, 19.11 s] Q.2 A particle of mass 1 kg is acted upon by a force 'F' which varies as shown in Fig. 9.3.26. If initial velocity of particle is 10 m/s, determine i) The maximum velocity of the particle ii) Time when particle will be at the point of reversal. [Ans. : i) 110 m/s ii) 3.16 s] 7. Conservation of Momentum • If there are two objects A and B connected by a rope then impulse-momentum theorem can be applied for each object. For A, • The force in the rope connecting A and B is equal in magnitude for both A and B but has opposite direction. If no other external force acts on them or the external forces are equal in magnitude but opposite in direction, then Adding equations (9.3.16) and (9.3.17), • If initial velocities are replaced by This equation represents the conservation of momentum. • Note that conservation of momentum principle can be applied in situations where the external forces acting on a system of particles cancel each other, • The internal forces being equal in magnitude but opposite in direction, will always cancel each other. Solved Examples for Understanding Example 9.3.21 A 40 kg block A is connected to a 60 kg block B by a spring of constant k = 180 N/m. The blocks are placed on a smooth horizontal surface and are at rest when the spring is stretched 2 m. If they are released from rest, determine the speeds of blocks A and B, at the instant the spring becomes unstretched. Solution: When spring is released, A moves towards right and B moves towards left. By conservation of momentum, By conservation of energy, Example 9.3.22 A gun of a share battery is nested by three springs, each of constant 250 kN/cm as shown. The gun has 80 Mg mass and fires 500 kg shell with a muzzle velocity 1000 m/s. Calculate total recoil of gun and maximum force developed in each spring. Solution: By conservation of momentum, By conservation of energy, Example 9.3.23 A 900 kg car travelling at 48 km/h couples to a 680 kg car travelling at 24 km/h in the same direction. Determine their common velocity after coupling. What is the amount of energy lost? Solution: As collision is plastic, v1 = v2 = v By conservation of momentum, Example 9.3.24 A 45 Mg rail car moving at 3 km/h is to be coupled, to a 25 Mg car which is at rest. Determine average impulsive force acting on each car during coupling process which lasts for 0.3 s. Also find final velocity of coupled cars. Solution : By conservation of momentum, As the collision is plastic, v1 = v2 = v By impulse-momentum theorem for 25 Mg car, The same result can be obtained using impulse momentum theorem for the 45 kg car with a negative sign as the force on the two cars will have same magnitude but opposite direction. Example 9.3.25 An airline employee throws a 12 kg suitcase with horizontal velocity 2.5 m/s onto a 30 kg baggage carrier. If carrier is initially at rest and can roll freely, find velocity of carrier after the suitcase has slid to a relative stop on the carrier. What is the ratio of final kinetic energy of carrier and suitcase to the initial kinetic energy of suitcase? Solution: By conservation of momentum, (12) (2.5) + 03 4 (30 + 12)v where v is the common velocity of the baggage carrier and the suitcase ⸫ v = 0.7143 m/s Final kinetic energy of carrier and suitcase Examples for Practice Q.1 A swimmer of mass 70 kg jumps from a stationary boat of mass 50 kg with a velocity having a horizontal component of 3 m/s. Determine the velocity of the boat after the swimmer jumps off. [Ans. : 4.2 m/s] Q.2 A 50 kg man standing on a frozen lake throws a 1 kg stone with a velocity of 20 m/s. Determine the distance that the man will move if the coefficient of friction is 0.01. [Ans. : 0.815 m] 8. Direct Central Impact • Impact is a collision between two objects which occurs in a very small interval of time during which the colliding objects exert large forces on each other. • The common normal to the surfaces in contact during the impact is known as line of impact. • If the velocities of both objects are along the line of impact, the impact is called direct central impact. If velocity of one or both objects is at an angle with line of impact, it is called oblique impact. • Consider direct central impact of two objects A and B moving with velocities vA and vв (uA > uB) as shown in Fig. 9.3.30 (a). • During impact, a force P is exerted on A towards left and on B towards right due to which they get deformed. • After maximum deformation, the objects start regaining their original shape. The time during which the objects regain their original shape is called the time of restitution. In general, the force R exerted by B on A during restitution is different from the force P exerted during deformation. • By impulse-momentum principle during period of deformation, and during period of restitution • The ratio of magnitude of impulse during the period of restitution to the magnitude of impulse during the period of deformation is called the coefficient of restitution denoted by e. From (9.3.26), we can define the coefficient of restitution as the negative ratio of relative velocity after collision to the relative velocity before collision. For perfectly elastic collision, where kinetic energy and momentum are both conserved, e = 1. For plastic collisions, where both objects move together with same velocity after collision, e = 0. For other collisions, 0 < e < 1. Note that momentum is conserved in all types of collisions. General Procedure for Solving Problems 1) Use conservation of momentum equation. ii) Use coefficient of restitution equation. iii) Solve the two equations to solve for the two unknown velocities after impact. iv) If energy imparted to an object during impact is converted to another form or dissipated in friction, use conservation of energy or work-energy principle for further analysis. v) For collision of an object with a rigid surface like the ground, the velocity of rigid surface before and after impact is zero. i.e., velocity after impact is 'e' times the velocity before impact in opposite direction. Example 9.3.26 A ball of mass 20 kg moving with a velocity of 5 m/s strikes directly another ball of mass 10 kg moving in the opposite direction with a velocity of 10 m/s. If the coefficient of restitution is equal to 5/6, then determine the velocity of each ball after impact. Solution: m1 = 20 kg, u1 = 5 m/s m2 = 10 kg, u2 = -10 m/s e = 5/6 By conservation of momentum, From (1) and (2), Example 9.3.27 Two blocks approaching each other along smooth surface, along same line are as shown. After impact, velocity of B is observed to be 2.5 m/s to the right. Determine coefficient of restitution. Solution : By conservation of momentum, Example 9.3.28 Perfectly elastic balls A, B and C of masses m, 2 m and 4 m respectively are moving along the same straight path with velocities 4v, v and 0.75 v respectively. Ball A strikes ball B and then ball B strikes ball C. Prove that balls A and B are brought to rest during these impacts. Solution: For collisions we have to use two equations-conservation of momentum and coefficient of restitution. For collision between A and B, For perfectly elastic collision, e = 1. Adding equations (1) and (2), we get 3vB = 9v ⸫ vB = 3v From equation (2), -vA + 3 v = 3 v i.e., A is brought to rest after collision with B and B starts moving with velocity 3 v. For collision between B and C, Adding equation (3) and (4), 3vC = 6.75 v ⸫ vC = 2.25 v Form equation (4), -vB + 2.25 v = 2.25 v i.e., B is brought to rest after collision with C. Example 9.3.29 Two identical cars B and C are at rest on a loading dock with their brakes released. Car A of same model is pushed by workers, hits car B with velocity 1.5 m/s, causing series of collisions between three cars. Assuming e = 0.50 for impact between A and B, while e = 1.0 for impact between B and C, find velocity of each car after all collisions have taken place. Solution: Let mass of each car be m. For collision between A and B, From equations (1) and (2), vA = 0.375 m/s → vB = 1.125 m/s → For collision between B and C,. From equations (3) and (4) vB = 0 vC = 1.125 m/s → As A is moving towards right at 0.375 m/s and B is stationary, there will be another collision between A and B. From equations (5) and (6), vA = 0.09375 m/s → vB = 0.28125 m/s → Now there is no further collision as vA < vB < vC and all the three are moving towards right. Example 9.3.30 A small rubber ball is released from a height of 80 cm on a horizontal floor. After the first bounce it rises to a height of 48 cm. Compute the coefficient of restitution. Upto what height it will rise after the second bounce ? Solution: Velocity of ball before first impact is With this initial velocity, ball rises to a height of 48 cm = 0.48 m After first impact, ball has velocity v1 = 3.962 × 0.7746 = 3.069 m/s ↑ The ball will return to the ground with same velocity. ⸫ Velocity of ball before second impact is u2 = 3.069 m/s ↓ Velocity after second impact, v2 = e u2↑ v2 = 0.7746 × 3.069 = 2.377 m/s ↑ with this initial velocity, the ball will rise to height Example 9.3.31 A mass 10 kg travelling towards right
with a speed of 25 m/s collides with another mass 20 kg travelling in the same
direction with a speed of 9 m/s. If the co-efficient of restitution is 0.6,
find the velocities of masses after collision and loss in kinetic energy. What
is the impulse on either mass? Solution: Let
v1 and v2 be the velocities of the two blocks after
collision and u1 and u2 before collision.
By
conservation of momentum, Examples for Practice Q.1 A ball is dropped from a height of 2 m on a smooth floor. The height of ball after the first bounce is 1.62 m. Find the height after the second and third bounces and also the coefficient of restitution between the ball and the floor. Take g = 9.8 m/s2. [Ans. : h2 = 1.31 m, h3 = 1.061 m, e = 0.9] Q.2 Three perfectly elastic balls A, B and C of masses 2 N, 6 N and 12 N are moving in the same direction with velocities 12 m/s, 4 m/s and 2 m/s respectively. If ball A strikes B, which in turn strikes C, prove that the balls A and B. will be brought to rest after impact. 9. Oblique Impact • If the velocities of the two colliding bodies are not along the line of impact, the impact is said to be oblique. • Consider oblique impact of two bodies A and B as shown in Fig. 9.3.34. • μA and μB are velocities of A and B respectively before impact and vA and vB after impact. • During impact, the internal forces are directed only along the line of impact. • Hence the components of the two velocities will change only along the line of impact. The components of velocities along the common tangent remain unchanged. • Momentum is conserved along the line of impact. • The relative velocities along line of impact are related to the coefficient of restitution. • Equations (9.3.29) and (9.3.30) can be solved simultaneously to find (vA)n and (vB)n. Knowing (vA)t and (vB)t from equations (9.3.27) and (9.3.28), the velocities of A and B can be calculated after impact. Example 9.3.32 A smooth spherical ball A of mass 15 kg is moving from left to right with a velocity of 5 m/s in a horizontal plane. Another identical ball B travelling in a perpendicular direction with a velocity of 15 m/s collides with A in such a way that the line of impact is in the direction of motion of ball A. Assuming e = 0.6, determine the velocity of balls A and B after impact. Solution: The collision is shown in Fig. 9.3.35. As the velocity components remain unchanged along the t-axis, (vA)t = 0 and (vB)t = 15 m/s By conservation of momentum along n-axis, Adding equations (1) and (2), 2(vB)m = 8 ⸫ (vB)m = 4 m/s Substituting in equation (1), Example 9.3.33 A ball of mass 1 kg moving with a velocity of 6 m/s strikes another ball of mass 2 kg moving with a velocity of 2 m/s at the instant of impact the velocities of the two balls are parallel and inclined at 30° to the line joining their centers as shown in the Fig. 9.3.36. If the coefficient of restitution is 0.5, find the velocity and the direction of the two balls after impact. Also calculate the loss in kinetic energy due to impact and the percentage of loss. Solution: The t-axis along the common tangent and the n-axis perpendicular to it are shown in Fig. 9.3.36 (a). Resolving the initial velocities of A and B along t and n-axis. The t-component of velocity remains unchanged after impact. Momentum is conserved along the n-axis. The coefficient of restitution is given by From equations (1) and (2), (vA)n = 1.732 m/s (vB)n = 3.464 m/s Example 9.3.34 A ball of mass 2 kg, moving with a velocity of 3 m/s, impinges on a ball of mass 4 kg moving with a velocity of 1 m/s. The velocities of the two balls are parallel and inclined at 30° to the line of joining their centres at the instant of impact. If the coefficient of restitution is 0.5, find i) Direction, in which the 4 kg ball will move after impact ; ii) Velocity of the 4 kg ball after impact ; iii) Direction, in which the 2 kg ball will move after impact ; iv) Velocity of the 2 kg ball after impact. Solution: The t-axis along the common tangent and the n-axis perpendicular to it are shown in Fig. 9.3.37 (a). Resolving the initial velocities of A and B along t and n-axes, The t-component of velocity remains unchanged after impact. Momentum is conserved along the n-axis. The coefficient of restitution is given by From equations (1) and (2), Example 9.3.35 Two smooth spheres 1 and 2, having a mass of 2 kg and 4 kg respectively collide with initial velocities as shown in Fig. 9.3.38, If the coefficient of restitution for the spheres e = 0.8, determine the velocities of each sphere after collision. Solution: The t-axis along common tangent and tangent and the n-axis perpendicular to it are shown in Fig. 9.3.38 (a).. Resolving the initial velocities of A and B along t and n-axis, The t-component of velocity remains unchanged after impact. Momentum is conserved along the n-axis i.e., The coefficient of restitution is given by, Adding equations (1) and (2), From equation (1), Example for Practice Q.1 A ball strikes the rigid floor at an angle of 60o as shown in Fig. 9.3.39. Determine the velocity of the ball after impact if e = 0.70. (Ans. : 6.29 m/s, 50.5°Kinetics Energy and Momentum Methods
![]() acts on a particle which undergoes a displacement
acts on a particle which undergoes a displacement ![]() from A to B at an angle θ with
from A to B at an angle θ with ![]() as shown in Fig. 9.3.1 then the work done is
as shown in Fig. 9.3.1 then the work done is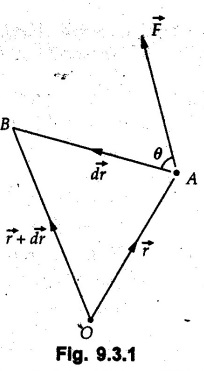
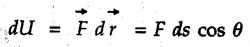
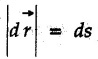 is the magnitude of displacement. If the particle is taken from position 1 to position 2 and the force is variable, the total work done is
is the magnitude of displacement. If the particle is taken from position 1 to position 2 and the force is variable, the total work done is
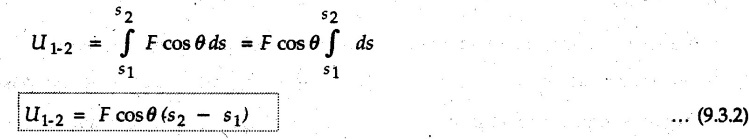
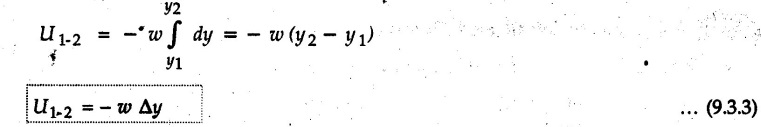
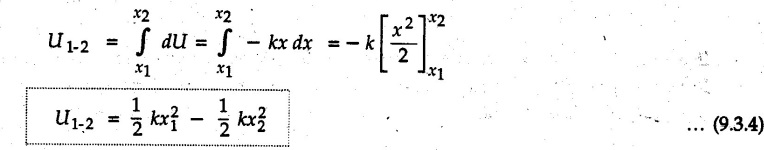
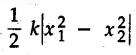 and then assigning positive or negative sign depending upon the directions of spring force and displacement.
and then assigning positive or negative sign depending upon the directions of spring force and displacement.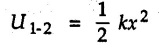
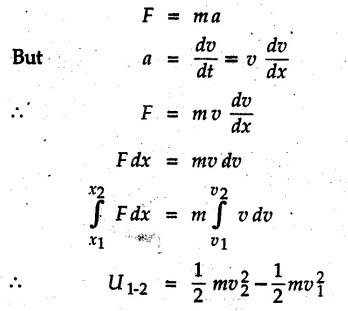

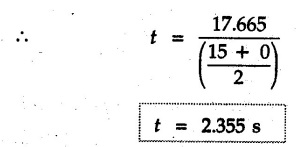
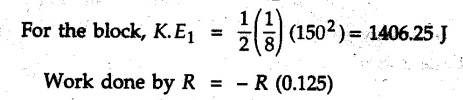

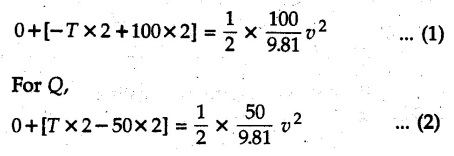

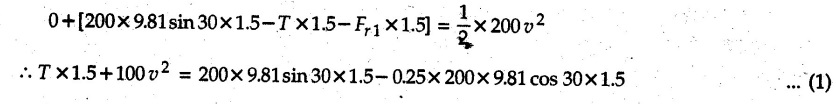

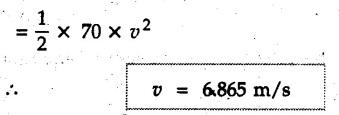


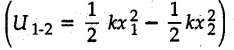 depends only on positions x1 and x2 and hence spring force is a conservative force.
depends only on positions x1 and x2 and hence spring force is a conservative force.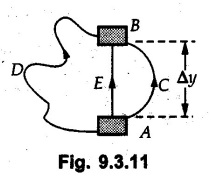
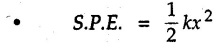
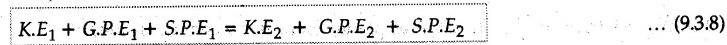

Solved Examples for Understanding
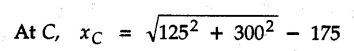
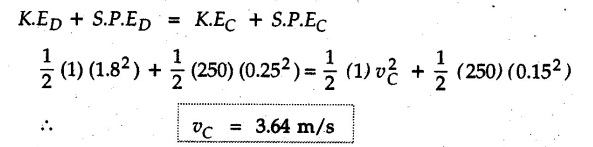
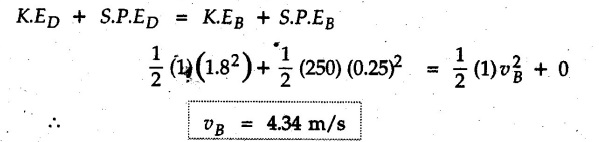
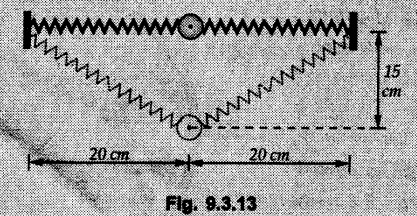
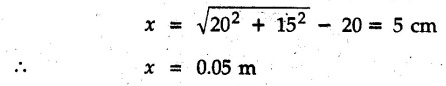
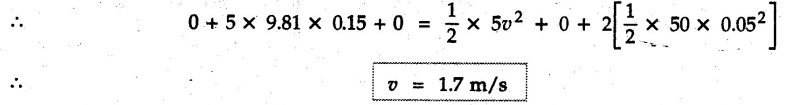
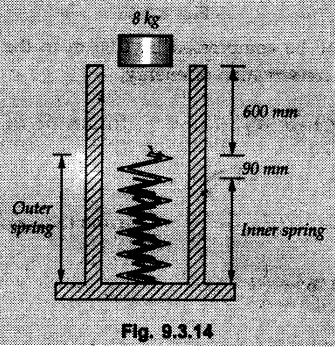
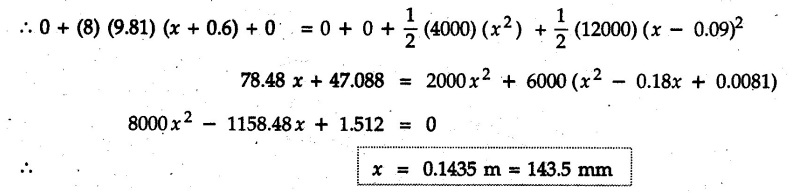

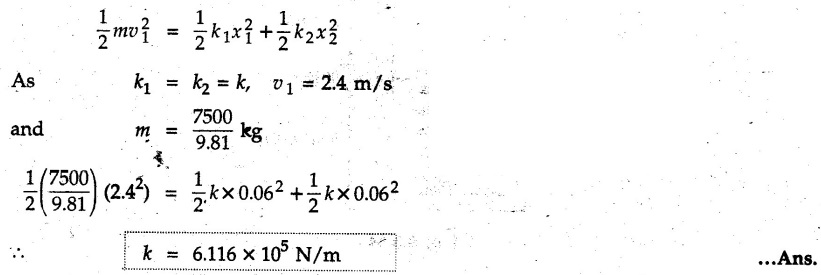


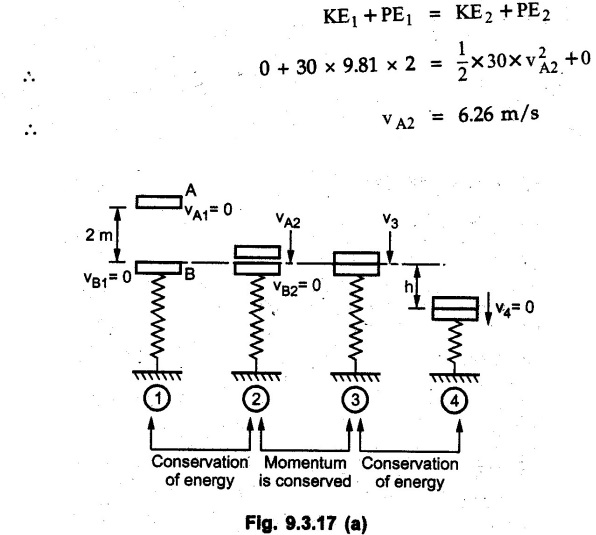
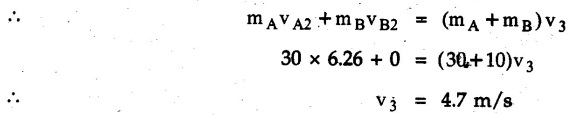
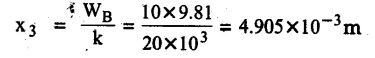
 • Solving the above equation, we get
• Solving the above equation, we get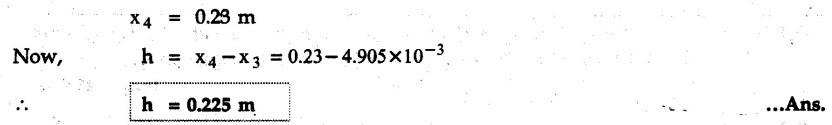
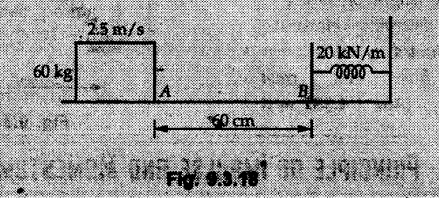
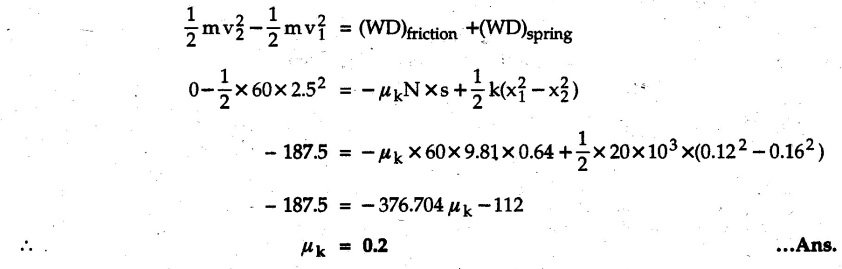
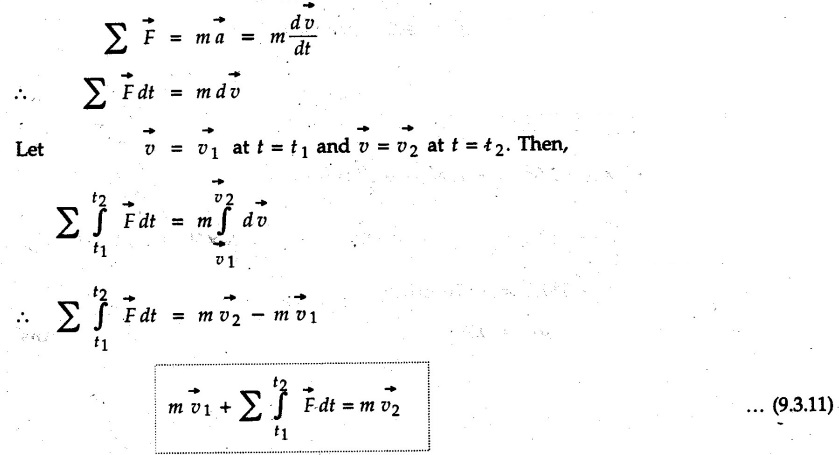
![]() is defined as the linear momentum and
is defined as the linear momentum and 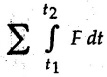 is defined as the impulse.
is defined as the impulse.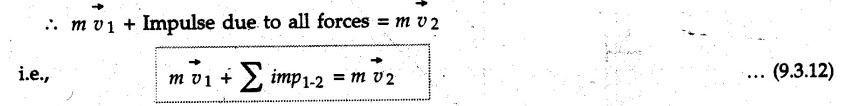
![]()

Solved Examples for Understanding
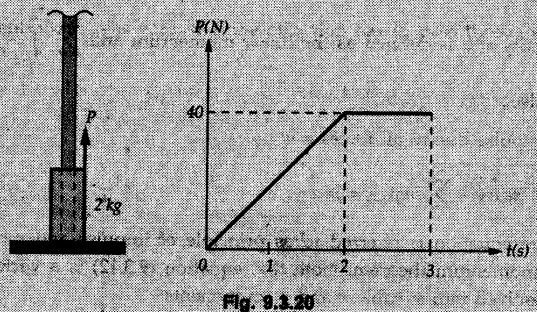
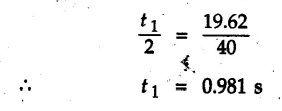





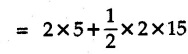
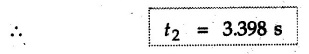




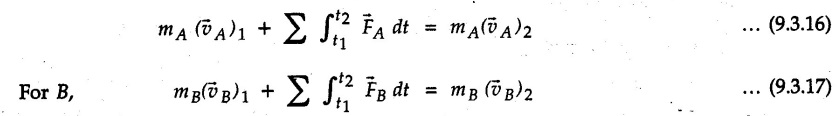
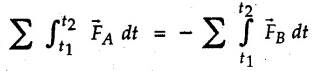

![]() and final velocities by
and final velocities by ![]()

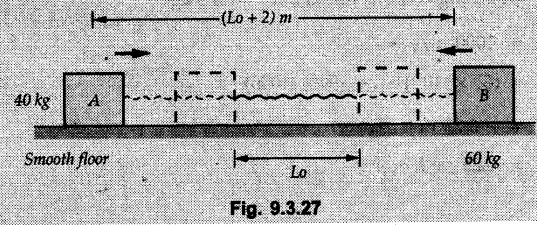


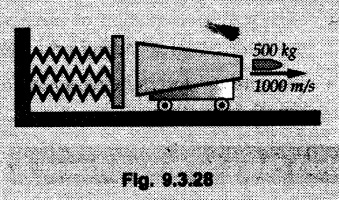
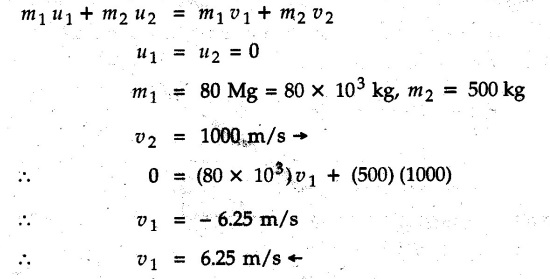


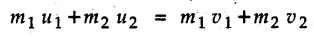

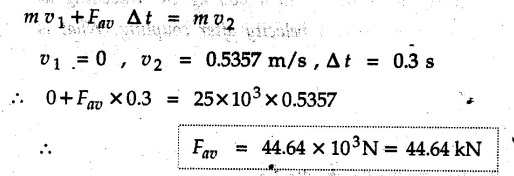
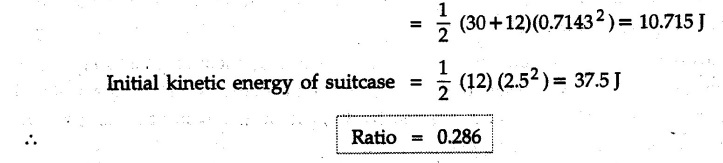
IMPACT OF BODIES



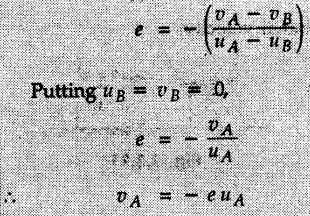
Solved Examples for Understanding
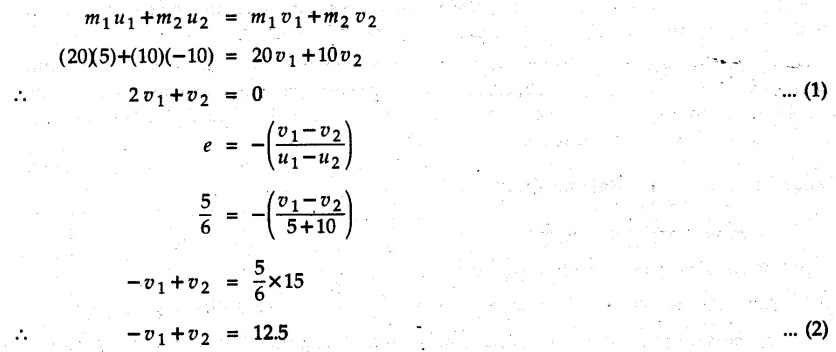


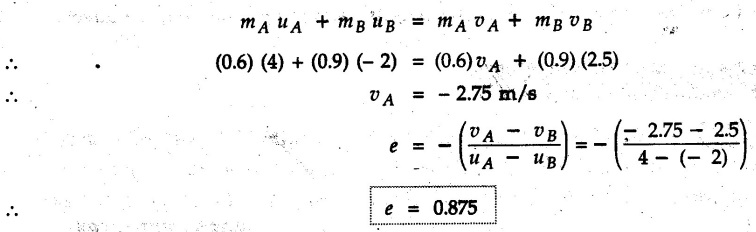
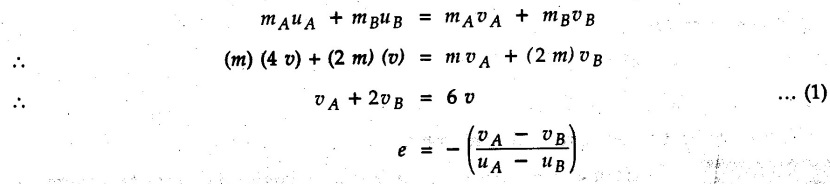


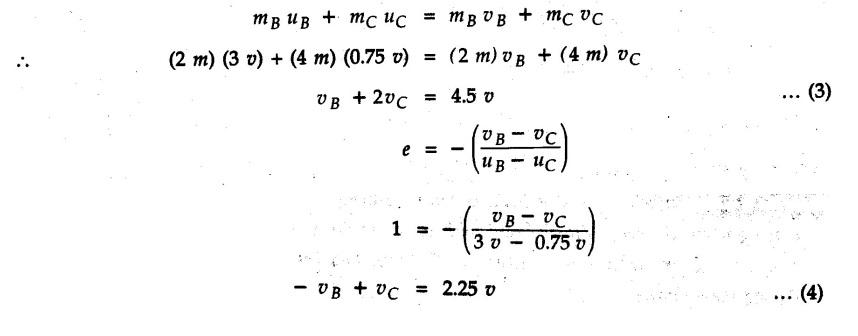
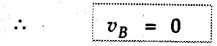


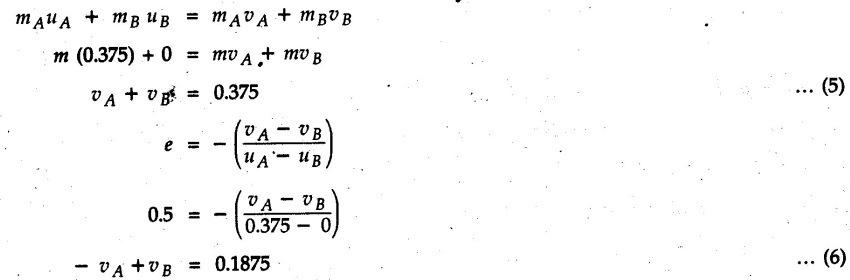

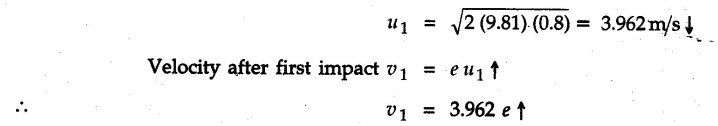
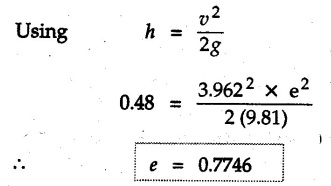





Solved Examples for Understanding


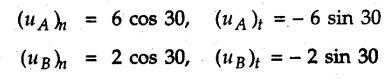



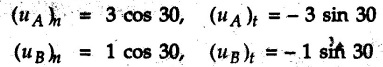
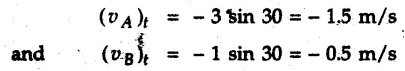
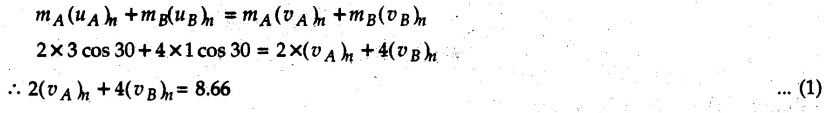
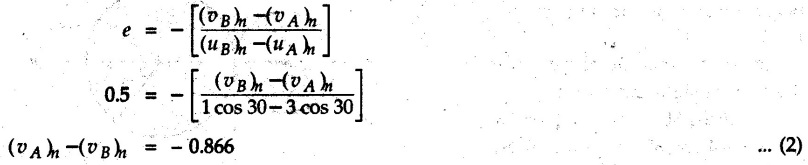
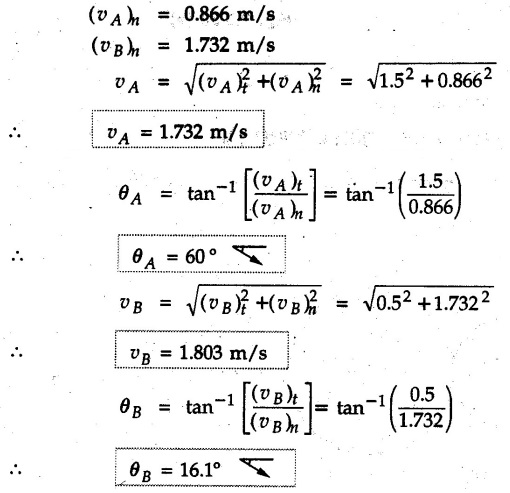

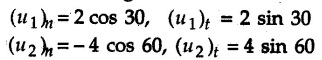
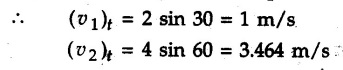
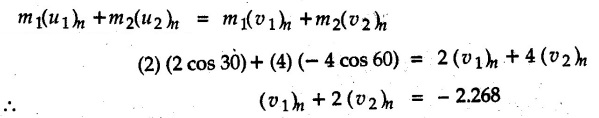
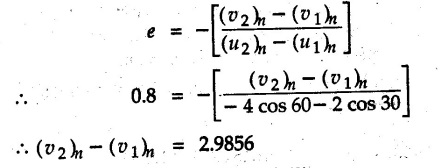
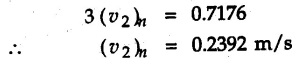

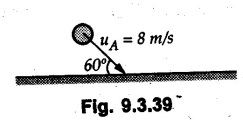
![]() )
)
Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : with Solved Example Problems - Kinetics - Energy and Momentum Methods
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
