Engineering Physics: Unit I: Mechanics
Kinetic Energy of the system of particles
Let there be n number of particles in a system of particles and these particles possess some motion.
KINETIC ENERGY OF THE SYSTEM OF PARTICLES Let there be n number of particles in a system of particles and these particles possess some motion. The motion of the ith particle of this system depends on the external force Let at any time the velocity of ith particle be Let where Differentiating the equation 2 we get where vi is the velocity of ith particle and vCM is the velocity of centre of mass of system of particle. Putting equation 3 in 1 we get, The sum of kinetic energy of all the particles can be obtained from equation 4 Now last term in equation (5) is equal to zero Therefore, kinetic energy of the system of particles is, is the kinetic energy obtained as if all the mass were concentrated at the centre of mass is the kinetic energy of the system of particle w.r.t. the centre of mass. Hence it is clear from equation (6) that kinetic energy of the system of particles consists of two parts: the kinetic energy obtained as if all the mass were concentrated at the centre of mass plus the kinetic energy of motion of all particles about the centre of mass. If there were no external force acting on the particle system then the velocity of the centre of mass of the system will remain constant and kinetic energy of the system would also remain constant.![]() acting on it.
acting on it.![]() then its kinetic energy would be
then its kinetic energy would be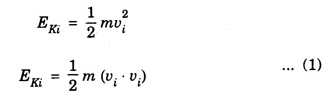
![]() be the position vector of the ith particle w.r.t. O and
be the position vector of the ith particle w.r.t. O and ![]() be the position vector of the centre of mass w.r.t.
be the position vector of the centre of mass w.r.t. ![]() , as shown in the figure 1.16, then
, as shown in the figure 1.16, then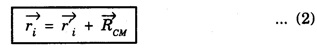
![]() is the position vector of centre of mass of the system w.r.t. O.
is the position vector of centre of mass of the system w.r.t. O.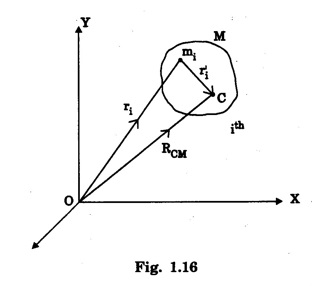
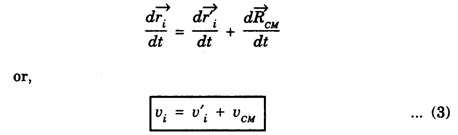
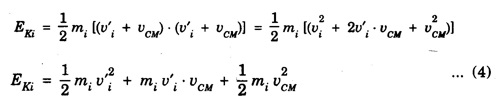
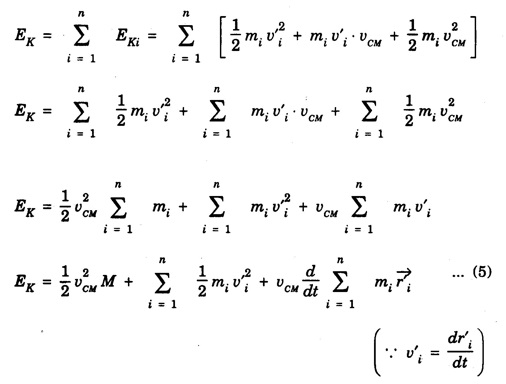
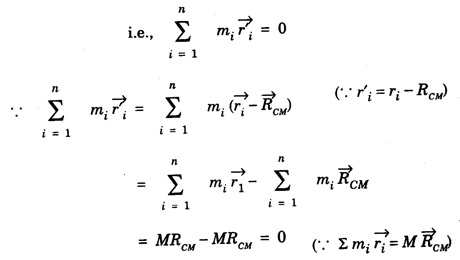
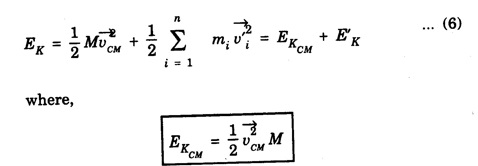
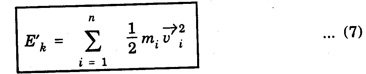
Engineering Physics: Unit I: Mechanics : Tag: : - Kinetic Energy of the system of particles
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
