Engineering Mechanics: Unit V: Dynamics of Particles
Kinematics - Rectilinear Motion
with Solved Example Problems
• Rectilinear kinematics deals with the following variables a) Position b) Displacement c) Distance travelled d) Velocity e) Acceleration
KINEMATICS - RECTILINEAR MOTION • Rectilinear kinematics deals with the following variables a) Position b) Displacement c) Distance travelled d) Velocity e) Acceleration a) Position: • To define position of a particle moving along a straight line, only one co-ordinate is sufficient as that line can be chosen as the X or Y-axis. • Thus motion of a particle in a straight line is a one dimensional problem. • An origin has to be chosen on that line and a direction on one side of that origin has to be taken as positive. • Generally, for a horizontal line (the X-axis) the right side of origin is taken positive and left side negative. For a vertical line, above the origin is taken positive and below the origin negative. For inclined line, one can use a sign convention according to convenience. • Position is a vector quantity as it has both magnitude and direction. • In one-dimension, vector quantities are represented by scalars with positive or negative sign representing their direction. • For example, a position of - 5 m on a horizontal line indicates a position 5 m to the left of the origin. b) Displacement : • It is defined as the change in position. Displacement is also a vector quantity. Displacement = Final position - Initial position. • Note that the position is defined at a particular instant of time, whereas displacement is defined in a finite, non-zero time interval. • The displacement and position at a particular time will be same if the particle starts from origin, i.e, the initial position is zero. • For motion along the horizontal, if final position is to the right of the initial position the displacement will be positive. For vertical motion, displacement is positive when final position is above the initial position and negative when final position is below the initial position. c) Distance travelled : • It is positive scalar quantity which represents the total length of the path covered by the particle. • It can be obtained from displacement. • The magnitude of displacement in any time interval is equal to the distance travelled only when the particle keeps travelling in the same direction throughout that time interval. • If the particle changes direction, split the time interval into suitable smaller intervals so that in each smaller interval, the partical travels in a particular direction. • The total distance travelled can then be obtained by adding magnitudes of displacements in all these intervals. • To illustrate the difference between the three quantities - position, displacement and distance travelled, consider a particle starting from position x1 at time t1, travelling to the right to reach position x2 at time t2 and then travelling to the left to reach position x3 at time t3 as shown in Fig. 9.1.1. • Then, at time t3, position = x3. Displacement = x3 - x1 Distance travelled = | x2 - x1 | + | x3 - x2 | d) Velocity: • If a particle has displacement Ax in a time interval At, then the average velocity is given by • The instantaneous velocity, which is generally referred to as velocity is given by instantaneous velocity = • Velocity is a vector quantity and in rectilinear motion will be represented by a scalar with positive or negative sign indicating its direction. • The magnitude of velocity is known as speed. e) Acceleration : • If the velocity of particle changes by Δv in a time interval Δt, the average acceleration is given by • The instantaneous acceleration, generally referred to as acceleration is given by • The above equation can also be written as • The acceleration is a vector quantity and in rectilinear motion, it will be represented by a scalar with positive or negative sign indicating its direction. • The term deceleration is used to indicate that the speed (the magnitude of v) is decreasing. • If 'v' and 'a' are in same direction it is acceleration whereas if 'v' and 'a' are in opposite directions, there is deceleration. • For example, when an object is thrown upwards (initial velocity upwards) then the object gets decelerated as the acceleration due to gravity is downwards. When an object is thrown downwards it gets accelerated as the initial velocity and the acceleration are both directed downwards. • Thus if 'a' and 'v' have the same sign, it is acceleration and if they have opposite sign, it is deceleration. • Problems in kinematics of rectilinear motion can be broadly classified into the following types : i) Variable acceleration where functions are given relating any two of the four variables position, velocity, acceleration and time. ii) Motion with constant acceleration. This type includes motion under gravity. iii) Variable acceleration when functions are not known or the function changes from one time interval to another. In such cases, motion diagrams are used which are graphs relating any two of the four variables. iv) Dependent motion where variables for one object are related to variables of another object. v) Relative motion. • We now discuss these in the subsequent articles. When functions relating any two of the four variables are given, use basic definitions (equations (9.1.2), (9.1.4), (9.1.5) and (9.1.6)) and differentiate or integrate the functions to obtain relations for the required variables. • For example, if velocity is given as a function of time, v = f(t) then to get position 'x' in terms of 't', use v = dx/dt = f(t), • Separate the variables, dx = f(t) dt and integrate to obtain relation between 'x' and 't'. • One can use either definite or indefinite integration. If definite integration is used, to obtain an equation for x in terms of t, use limits of integration as say x0 to x for the variable 'x' and t0 to t for the variable 't' where x0 and t0 are then two initial values. • If indefinite integrals are used, the constant of integration has to be calculated usin some given conditions and then resubstituted to get the required equation. • If acceleration is given as a function, either a = dv/dt or a = dv/dx has to be used. In such cases we have to use that equation which enables us to separate the variables. i) Displacement and position are same when starting position is origin. Hence in situations where starting position is not known, it is convenient to take the starting position as origin. ii) The magnitude of displacement is equal to distance travelled only when particle keeps travelling in the same direction. iii) Whenever particle changes its direction in rectilinear motion, its velocity at that instant becomes zero. At the point where particle changes direction, it reaches its maximum or minimum value of position co-ordinate 'x'. ⸫ dx/dt = 0 ⸫ v = 0 iv) Condition for maximum or minimum velocity is dv / dt = 0, i.e., a = 0 v) To calculate distance travelled, first put v = 0 to find whether particle changes direction or not in the given time interval. vi) A linear relation between two variables, say when v varies linearly with t, is of the form v = mt + c. vii) When a vector quantity is proportional to another veetor quantity, the constant of proportionality can be either positive or negative depending upon directions of the two vectors. Example 9.1.1 A body moves along a straight line so that its displacement from a fixed point on the line is given by s = 3t2 + 2t. Find the velocity and acceleration at the end of 3 seconds. Solution: Example 9.1.2 A point P moves along a straight line according to the equation x = 4t3 – 2t - 5 where x is in metres, t is in seconds. Determine the velocity and acceleration when t = 3 sec. Solution : Example 9.1.3 The velocity of a particle is given by v = 4t3 – 5t2. When does the acceleration of the particle become zero? Solution : Example 9.1.4 The velocity of a particle is given by v = 2t3 + 6t2. Find the distance travelled by it while its velocity increases from 8 m/s to 108 m/s. Solution : The other roots are imaginary. When velocity increases from 8 m/s to 108 m/s, t changes from 1 8 to 3 s. Example 9.1.5 A particle moves along a straight line with variable acceleration. If the displacement is measured in m, and given by the relation in terms of time t, as S = 3t3 + 2t2 +7t + 3. Determine the displacement, velocity and acceleration of the particle at start and after 3 seconds. Solution: s = 3t3 + 2t2 + 7t + 3 Example 9.1.6 A particle travels along a straight line towards a given point O. The velocity 'o' of the particle is proportional to the distance 's' of the particle from point O. Initially the particle is at a distance s0 from the point O. Express the distance 's' in terms of time 't'. Solution: It is given that ν ∝ s If the position is towards right of O, the velocity is towards left. If postion is towards left of O, the velocity is towards right. (Refer Fig. 9.1.2 (a)) i.e., if position is positive then velocity is negative and vice versa. Example 9.1.7 The acceleration of a particle moving along a straight line decreases uniformly from 12 m/s2 to zero in 10 s, at which time its velocity is 10 m/s. Find its initial velocity and change in position during the 10 s interval. Solution : As acceleration decreases uniformly with time, the relation between acceleration and time is linear. ⸫ a = mt + c At t = 0, a = 12m/s2 ⸫ 12 = m(0) + c ⸫ c = 12 At t = 10 s, a = 0 ⸫ 0 = m(10) + 12 To find initial velocity 'v0', we use To find change in position, first we find a relation between 'v' and 't'. Example 9.1.8 Displacement of particle having rectilinear motion is given as x = 0.333t3 - 2.65t2 + 5.7 t + 1.2(m) find position of particle and distance travelled by it at t = 4 seconds. Solution: The position at t = 4 is To calculate distance travelled, we have to find if the particle changes direction by putting v = 0. We split the time interval from 0 to 4 s into 3 parts: 0 to 1.5 s, 1.5 s to 3.806 s and 3.806 s to 4 s Example 9.1.9 A particle starts from rest at the origin and is given an acceleration Solution : For maximum velocity, a = 0 From equation (1), putting x = ∞, K = 750, and v = vm, Example 9.1.10 Rectilinear motion of a particle is described by equation a = 0.4 V where a and v are in mm/s2 and mm/s respectively. If v = 30 mm/s at t = 0, find the distance travelled by particle before coming to rest. Solution: Example 9.1.11 A particle starts with initial velocity 12 m/s from origin and moves with acceleration a = A - Bt along a straight line. Find values of constants 'A' and 'B', if particle covers 60 m distance in 5 seconds and stops. Also obtain expressions for velocity and displacement. Solution : At t = 5 s, v = 0; x = 60 m ⸫ From equation (1) and (2), we get From equations (3) and (4), The units for A and B are obtained using dimensional analysis of equation a = A - Bt. Substituting in (1) and (2), Example 9.1.12 A particle moves along a straight path in a viscous median with acceleration a = 2/x2 where 'a' is in m/s2 and 'x' in m. Knowing that x = 1m and v = 2 m/s, at t = 1 s, determine the position and velocity of the particle at t = 4 s. Solution: Example 9.1.13 Reclinear motion of a particle is governed by equation a c. 0.09 x = 0. Knowing that v = 0 and x = 1 m at t = 0, Obtain expressions for position and velocity. Hence, find velocity at t = 5's and position at t = 10 s. What type of motion is it ? Solution: Given: a + 0.09 x = 0 This equation represents Simple Harmonic Motion. In equation (1), 'v' is expressed in terms of x. 'v' can also be expressed in terms of t as v = dx/dt. From equation (2), In the above equation the angle is in radians. Note that if 'v' is calculate from equation (1) by first calculating 'x' at t = 5 s, we have to decide whether to take positive or negative root as square root has been taken. Hence we calculate 'v' from equation (3) which will give 'v' with proper sign indicating it's direction in S.H.M. At t = 10 s, x = cos (0.3 × 10) Example 9.1.14 Acceleration of a particle is a = 9 - 3 t2, knowing that x = 5 m and v = 0 at t = 0, find position, velocity and distance travelled when t = 4 s. Solution : To calculate distance travelled, first find whether particle has changed direction in the given time period by substituting v = 0 in equation (1). 9t - t3 = 0 t(9 - t2) = 0 ⸫ t = 0, t = ± 3 t = 3 s. As the particle changes its position at t = 3 s, split the time interval from 0 to 4 s into two parts, 0 to 3 s and 3 s to 4 s. In each of these time intervals, magnitude of displacement is equal to distance travelled. We can calculate the distance travelled alse by plotting how the particle moves as shown in Fig. 9.1.3. Particle travels from A to B and then from B to C. These distances are 25.25 – 5 = 20.25 m and 25.25 - 13 = 12.25 m ⸫ Total distance travelled = 20.25 + 12.25 = 32.5 m Example 9.1.15 Frictional resistance to the motion of a train moving on a level track when power has been cut-off is given as (a+bv2) m/s2, where 'a' and ' are constants. Find distance travelled by train before carrying to rest when power has been cut-off at 108 km/h. Take a = 0.07 and b = 0.001. Solution: Initial velocity is v = 108 km/h = 30 m/s Example 9.1.16 Acceleration of a particle moving along a straight line is directly proportional to time t'. At t = 0 s, velocity v = 300 mm/s. Knowing that v = 250 mm/s and x = 500 mm when t = 1 s, determine velocity 'v', position 'x' and distance travelled in 5 s. Solution : a ∝ t ⸫ a = kt To calculate distance travelled, first put v = 0 ⸫ - 50t2 + 300 = 0 t = 2.45 s ⸫ Particle changes direction at t = 2.45 s. ⸫ Distance travelled in 5 s = |x2.45 – x0| + |x5 − x2.45| From equation (2), Distance travelled = |706.56 - 216.67| + | -366.67 - 706.56 | = 489.89 + 1073.23 = 1563.12 mm Example 9.1.17 A particle starting from rest, moves in a straight line and its acceleration is given by a = 50 – 36t2 m/s2 where t is in sec. Determine the velocity of the particle when it has traveled 52 m. Solution : Integrating on both sides, Integrating on both sides, Assuming particle starts from origin, After solving the above equation, t = 2 sec or 2.08 sec. To check whether particle changes its direction of motion, put v = 0 in equation (i), v = 0 = 50t – 12t3 ⸫ t = 2.04 sec The particle moves in same direction till t = 2.04 sec. After t > 2.04 sec, the distance travelled is more than the magnitude of displacement. ⸫ At x = 52 m, t ≠ 2.08 sec ⸫ t = 2 sec Put in equation (i), v = 50 × 2 – 12 × 23 Examples for Practice Q.1 A particle starts from rest and moves along a straight line under an acceleration given by a = 4 – 1/6 t2 where a = Acceleration in m/s2 and t = Time in second find i) Velocity attained and the distance travelled in 4 seconds ii) When will the particle come to rest and what will be the distance it will have gone then. [ Ans. : i) v = 12.44 m/s, s = 28.44 m, ii) t = 8.485s, s = 72 m] Q.2 Equation of motion of a particle moving in a a straight line is given by s = 15t + 3t2 - t3, where s is distance moved and t is time in seconds. Find i) velocity and acceleration at the start ii) Time at which particle reaches maximum velocity. iii) Maximum velocity of the particle. [ Ans. : 1) Vo = 15 m/s αo = 6 m/s2 ii) t = 12 iii) Vmax = 18 m/s] Q.3 A particle starts with an initial velocity of 8 m/s and moves along a straight line. Its acceleration 'a' at any time 't' after start, is given by the expression a = λ - μt, where λ and μ are constants. Determine the equation for displacement if the particle covers a distance of 40 m in 5 seconds and stops. [ Ans. : • When acceleration is constant, using • As • The quantity x – x0 is the displacement 's' • Another expression for acceleration is • Separating the variables, • The three equations (9.1.7), (9.1.8) and (9.1.9) can be used only when it is known that acceleration is constant. Motion Under Gravity • Problems of motion under gravity can also be solved using these equations. • As this motion is in the vertical direction, we use the sign convention: Upwards positive and downwards negative. • According to this convention, acceleration will always be negative as gravitational acceleration (g) is always directed downwards. (a is replaced-by g) • Note that the quantity 's' that appears in these equations is displacement and not distance travelled. • Remember that displacement and distance travelled are same only when object keeps travelling in the same direction. In these problems, the starting position will be taken as origin. • If the final position is above the initial position, the displacement will be positive and if the final position is below the initial position, the displacement will be negative. • If the problem involves simultaneous motion of two objects, relate the variables of the two objects. • Here the equation of motion are, Displacement during nth second : • The displacement during nth second can be obtained by subtracting the displacement in (n − 1) seconds (Sn-1) from the displacement n seconds ($n). • Using Solved Examples for Understanding Example 9.1.18 A body starts with an initial velocity of 5 m/s and moves with a uniform acceleration of 1.5 m/s2. Find the velocity of the body after 8 seconds, Solution : u = 5 m/s a = 1.5 m/s2 t = 8 s. v = u + at = 5 + 1.5 × 8 Example 9.1.19 A bullet, moving at the rate of 250 m/s, is fired into wood. It penetrates to a depth of 40 cm. Find the acceleration of the bullet. Solution: u = 250 m/s, s = 40 cm = 0.4 m v = 0 v2 = u2 + 2a s 0 = 2502 + 2 a × 0.4 Example 9.1.20 A car travels with an initial velocity of 10 m/s and runs with a uniform acceleration of 0.5 m/s2. Find the distance travelled by the car in 8th second. Solution: u = 10 m/s, a = 0.5 m/s2 n = 8 Example 9.1.21 A train running at 80 km/n is brought to a standing halt after 50 seconds. Find the retardation and the distance travelled by the train before it comes to a halt. Solution: u = 80 km/h = 22.222 m/s v = 0 The retardation is 0.4444 m/s2. v2 = u2 + 2a s 0 = 22.2222 + 2 (-0.4444) s Example 9.1.22 Car A accelerates uniformly from rest on a straight level road. Car B starting from the same point 6 seconds later with zero initial velocity accelerates at 6m/s2. It overtakes the car A at 400 m from the starting point. What is the acceleration of the car A? Solution: For car A, Example 9.1.23 Two trains A and B leave the same station on parallel lines. A starts with a uniform acceleration of 0.15 m/s2 and attains the speed of 24 km/hour, after which, its speed remains constant. B leaves 40 seconds later with uniform acceleration of 0.30 m/s2 to attain a maximum speed of 48 km/hour. Its speed also becomes constant thereafter. When will B overtake A? Solution: Let t = Time for A when B overtakes it, and t1 = Time for A to attain speed of 24 km/h. During acceleration of A, ⸫ t1 = - 44.444 s A travels with constant velocity for t - 44.444 s. ⸫ Distance travelled by A is For B during acceleration, As B starts 40 s after A, it will travel for t – 40 - 44.444 = (t - 84.444)s with constant velocity. The distance travelled by B is Example 9.1 24 A stone is thrown vertically upwards from a point on a bridge located 40 m above the water. If it strikes the water 4 s after release, determine the speed at which the stone was thrown and the speed at which the stone strikes the water. Solution: Let u = Initial velocity of stone Example 9.1.25 A stone is thrown up vertically from the foot of a tower of height 22 m with a velocity of 12 m/sec. At the same time, another stone is dropped from the top of the tower. Find the height at which the two stones cross each other. Solution: Let the two stones A and B meet at height h from the ground as shown in Fig. 9.1.4. For A, Adding equations (1) and (2), Substitute in equation (1) Example 9.1.26 A ball is projected vertically upwards with a velocity of 20 m/s. Two seconds later, a second ball is projected vertically upwards with a velocity of 16 m/s. Find the height above the surface at which the two balls meet. Solution: For the first ball, u = 20 m/s, a = -9.8 m/s2 Let h = Height above the surface at which the two balls meet t = Time for the first ball when they meet ⸫ s = h For the second ball, From equations (1) and (2), 20t - 4.905 t2 = 35.62 t − 4.905 t2 - 51.62 51.62 = 15.62 t ⸫ t = 3.30474 Substitute in equation (1) h = 20 × 3.30474 - 4.905 × 3.304742 Example 9.1.27 A stone is dropped into a well. The sound of the splash is heard 3.63 seconds later. How far below the ground is the surface of water in the well? Assume the velocity of sound as 331 m/s. Solution: Let x = Depth of the well. Then displacement of stone s = -x Negative sign is for downward displacement. a = -g = -9.81 m/s2, t = Time and u = 0 for the stone. As total time is 3.63 s for stone to reach the water surface and sound to come up, the time for sound will be 3.63 - t. As sound travels with constant velocity, Distance travelled = Velocity × Time x = 331 × (3.63 - t). From equations (1) and (2), 4.905 t2 = 1201.53 – 331 t 4.905t2 + 331t - 1201.53 = 0 ⸫ t = 3.4533 s, - 70.94 s As t cannot be negative, t = 3.4533 s ⸫ From equation (1), Example 9.1.28 Three telegraph poles A, B and C are spaced at 50 m intervals along a straight road. A car starting from rest accelerates uniformly, passes post A and then takes 8 s to reach post B and further 7 s to reach post C. Calculate (a) The acceleration of the car (b) The velocity of the car at A, B, and C, (c) The distance of the post A from the starting point of the car. Solution: Let O be the starting point of the car as shown in Fig. 9.1.5. Let vA, vB and vC be the velocities of car at A, B and C respectively, x be the distance of post A from the starting point and a = acceleration of car. From equations (1) and (2), For motion from A to B, using v = u + at, vB = 5.774 + 0.119 × 8 For motion from B to C, vC = 6.726 + 0.119 × 7 For motion from O to A, using v2 = u2 + 2as, 5.7742 = 02 + 2(0.119) (x) Example 9.1.29 Elevators A and B in the adjoining shafts start moving in opposite directions with constant accelerations 0.3 m/s2 and 0.6 m/s2 respectively. 'A' moves down while 'B' moves up. If they were 150 m apart at t = 0, after what time they will be opposite to each other? How for each one has travelled ? Solution: When they are opposite to each other, Distance travelled by A is Example 9.1.30 A stone is thrown upward with a velocity of 40 m/s. Determine the time of Lone 30 A stone is thrown upward with a velocity the stone when it is at a height of 10 m and is moving downwards. Solution: We show here two methods for solution - one using scalar approach where the motion will be split into upward and downward motion and the second method using vector method. Method 1: In this method for upward motion a = -g and for downward motion. a = +g is taken. For upward motion upto the top, u = 40 m/s, v = 0, t = t1, Using v = u - gt, 0 = 40 - 9.81 t1, = t1 = 4.0775 s To calculate distance travelled during downward motion, first we have to calculate the maximum height 'h'. v2 = u2 – 2 g h ⸫ 0 = 402 – 2 (9.81) h h = 81.55 m ⸫ To reach 10 m height in downward motion, d = 81.55 - 10 = 71.55 m Let t2 = Time for downward motion. Using ⸫ t2 = 3:8193 s ⸫ The total time t = t1 + t2 = 4.0775 + 3.8193 Method 2 : In vector method we use sign convention: Upward positive and downward negative. a = -g = - 9.81 m/s2 Displacement s = + 10 m as final point is above the initial point. u = + 40 m/s 4.905 t2 – 40 t + 10 = 0 ⸫ t = 0.25826 s or 7.8968 s The smaller value of t is for upward motion and larger value for downward motion. Note: The vector method is a more efficient method for solving problems on motion under gravity. Example 9.1.31 In a flood relief area, a helicopter going up with constant velocity drops a food packet, which takes 4 seconds to reach ground. No sooner than the first packet reaches the ground, second packet was released, which takes 5 seconds to reach ground. From what height the first packet was released? Also find the constant, upward velocity of helicopter. Solution : Let u = Velocity of helicopter Initially, the velocity of packet will be same as velocity of helicopter. ⸫ Initial velocity of food packet = u Let h = Height from which the first packet is dropped. Then, the second packet will be dropped from height h + 4u as the helicopter will move distance 4u in 4 s. As final positions of the packets are below their initial positions. s1 = -h and s2 = - (h + 4u) t1= 4s and t2 = 5 s. a = -9.81 m/s2 for both packets. Example 9.1.32 A car runs with an initial velocity of 30 m/s and uniform acceleration of 3 m/s2. Find its velocity after 5 seconds. Solution: u = 30 m/s a = 3 m/s2, t = 5 s v = u + at ⸫ v = 30 + 3 × 5 Example 9.1.33 Water drips from a tap fitted to a barrel at the rate of four drops per second as shown in Fig. 9.1.8. Find the vertical separation between two consecutive drops after the lower drops has attained a velocity of 3 m/s. Solution: For B, v = 3 m/s↓ v = u + at -3 = 0 + (-9.81) t Example 9.1.34 A pall is projected vertically upward with a velocity of 9.8% m/s. Determine the maximum height travel by the ball, the velocity at which it strikes the ground and total time of journey. Solution: u = 9.81 m/s, v = 0, a = 9.81 m/s2, s = h v2 = u2 + 2 a s 0 = 9.812 + 2 (−9.81) h When the ball strikes the ground, s = 0 Example 9.1.35 A car comes to complete stop from an initial speed of 50 kmph in a distance of 100 m. With the same constant acceleration, what would be the stopping distance s from an initial speed of 70 kmph. Solution : Example 9.1.36 A stone is dropped from the top of a tower 50 m high. At the same time, another stone is thrown vertically upwards from the foot of tower with a velocity of 25 m/s. When and where the two stone cross each other? Solution: The conditions for the two stones A and B are shown in Fig. 9.1.10. Let t be the time when they meet. Substitute in equation (2) Example 9.1.37 A stone thrown vertically upward from earth returns to the earth in 5 sec. How high does the stone reached. Also determine the velocity with which it is thrown. Solution: A stone is thrown from earth and returns to earth hence displacement is zero i.e. Example 9.1.38 A body moving with uniform acceleration is observed to travel 33 m in 8th second and 53 m in 13th second of its travel. Calculate the velocity at start and uniform acceleration. Solution: Let the initial velocity of body is 'u' and acceleration is 'a'. As For first part of the motion travelled 33 m in 8 sec., The final velocity at the end of 8th second is, v = u + at = u + 8 a During 13th second of its travel, Example 9.1.39 A body A is projected vertically upwards from the top of a tower with velocity of 40 m/s, the tower being 180 m high. After t sec, another body B is allowed to fall from the same point. Both the bodies reach the ground simultaneously. Calculate t and the velocities of A and B on reaching the ground. Solution: For A, Example 9.1.40 Small steel balls fall from rest through the opening at A at the steady rate of two per second Fig. 9.1.11. Find the vertical separation h of two consecutive balls when the lower one has dropped 3 metres. Neglect air resistance. Solution: For the lower ball, u = 0, s = 3 m, a = 9.81 m/s2, t = t1 For the second ball, u = 0, a = 9.81 m/s2, t = 0.782 - 0.5 = 0.282 s Example 9.1.41 Two vehicles approach each other in opposite lanes of straight horizontal roadway as shown in Fig. 9.1.12. At time t = 0, the vechicles have the speeds and positions shown in the Fig. 9.1.12. Find the time and positions at which the vehicles meet if both continue to move with constant speed. Solution : If x be the distance of car A to reach meeting point C in time t then in same time bus B will travel (250 - x). As speed is constant for both, a = 0. Examples for Practice Q.1 Three marks A, B and C spaced at a distance of 100 m are made along a straight road. A car starting from rest and accelerating uniformly passes the mark A and takes 10 seconds to reach the mark B and further 8 seconds to reach mark C. Determine : i) Acceleration of the car ii) Velocity of the car at A and B iii) Distance of mark A from starting point. [Ans. : i) a = 0.278 m/s2 ii) vA = 8.611 m/s, vB = 11.391 m/s, iii) s = 133.36 m] Q.2 Two cars are travelling towards each other on a single lane road at velocities 12 m/s and 9 m/s respectively. When 100 m apart, both drivers realize the situation and apply their brakes. They succeed in stopping simultaneously and just short of colliding. Assume constant retardation for each car. Determine: i) Time required for cars to stop ii) Retardation of each car iii) Distance travelled by each car while slowing down. [Ans. : 1) 9.524 s il) 1.26 m/s2 and 0.945 m/s2 iii) 57.143 m and 42.857 m] Q.3 A stone is thrown vertically upwards with a velocity of 20 m/s from the top of a tower 25 m high. Calculate: i) The maximum height to which the stone will rise in its flight. ii) Velocity of stone during its downward travel at a point in the same level as the point projection. iii) Time required for the stone to reach the ground. Take 8 = 10 m/s2. [Ans. : i) 45 m ii) 20 m/s iii) 5 s] Q.4 A particle falls freely from the top of a tower and during the last seconts of its motion it falls 5/9 of the whole height. Find the height of the tower. Take g = 9.8 m/s2. [Ans. : 44.1 m] • Motion diagrams are graphs of any two of the 4 variables a, v, x and t. The more commonly required graphs are a-t, v-t and x-t, • a-t graph : The area under a-t graph is i.e. area under a-t graph gives change in velocity. The slope of tangent on a-t graph, which represents rate of change of acceleration is known as jerk. • v-t graph: The area under v-t graph is ⸫ Area under v-t graph gives change in position which is displacement. • Position can be obtained from a-t graph directly. We know that area under v-t graph gives change in position. • Let x0 and v0 be the position and velocity. respectively at t = 0 and x1 and v1 be the values at time t1. • Then, x0 - x0 = Area under v-t graph from 0 to t1. • Consider a general v-t graph as shown in Fig. 9.1.16 with initial velocity v0. The area consists of a rectangle with height v0 and the area above that enclosed by the curve. • The area above the rectangle can be obtained by considering a horizontal elementary strip of width dv and length t1 - t and then integrating this small elementary area from v0 to v1. • The integral represents the first moment of area under the a-t curve about t = t1. This method of finding x is called moment area method. • a-x graph : The area under a-x graph is • v-x graph: From v-x graph, we can obtain acceleration. • Thus to find acceleration from v-x graph at x = x1, draw tangent to v-x curve at x = x1 and draw perpendicular to the tangent. • The subnormal, i.e., the length on x-axis between the two points x = x1 and the point where the perpendicular drawn to the tangent intersects x-axis, gives acceleration. • When a-t graph is a straight line with positive slope as shown in Fig. 9.1.20 (a), if initial velocity v1 is given, the final velocity v2 can be calculated using v2 - v1 = Area under a-t graph. • The two points (t1, v1) and (t2, v2) can be plotted on v-t graph. To find the nature of v-t graph, we write equation of a-t graph as, a = mt + c • As a = dv / dt' which represents equation of a parabola. • On v-t graph, there will be parabola between the two points (t1, v1) and (t2, v2). The parabola has to be drawn with increasing slope of tangent as the slope of tangent on v-t graph represents acceleration which is increasing. • The slope of a line increases when it rotates anticlockwise. Hence the curve on v-t graph will be a parabola with increasing slope of tangent as shown in Fig. 9.1.20 (b). • If acceleration decreases with time, the slope of tangent on v-t graph has to decrease, i.e., tangent rotates clockwise. To find nature of curve on x-t graph, we write, • Integrating, we get ⸫ x-t graph will be a cubic curve as shown in Fig. 9.1.20 (c). • Again, slope of tangent on x-t graph represents velocity. If velocity increases, the tangent to x-t graph rotates anticlockwise and for decreasing velocity, the tangent rotates clockwise. • If acceleration is constant in the time interval from t1 to t2, • These graphs will be as shown in Fig. 9.1.22. • If a-t graph intersects the time axis as shown in Fig. 9.1.23 and Fig. 9.1.24, a = 0 at that instant. As a = dv/dt = 0, the velocity will be either maximum or minimum at that instant. The area below the x-axis is negative and above the x-axis is positive. • For Fig. 9.1.23, the velocity first decreases to a minimum and then increases. Also the tangent rotates anticlockwise on v-t graph which matches with the condition on a-t graph that acceleration is increasing. • Similarly, for the a-t graph shown in Fig. 9.1.24, the velocity becomes maximum at the instant acceleration becomes zero. • It should be noted here that the acceleration is zero only at a particular instant of time. If acceleration remains zero for some time interval, then velocity remains constant during that time interval. • While drawing x-t graph from v-t graph, the same rules are to be followed as discussed above for drawing v-t graph from a-t graph as the relations between a-t and v-t graph and v-t and x-t graph are same. Key Points to be Remembered while Solving Problems 1) Area under a-t graph gives change in velocity 2) Area under v-t graph gives change in position or displacement 3) Area under a-x graph gives 4) Slope of tangent to a-t graph gives jerk 5) Slope of tangent to v-t graph gives acceleration 6) Slope of tangent to x-t graph gives velocity 7) Position at time t1 can be obtained from a-t graph using moment-area method x1 = x0 + v0 t1 + Moment of area under a-t graph to the left of t1 about t1 Moment of area = Area × Distance of centroid from the point about which moment is taken 8) To obtain distance travelled, add magnitudes of all areas on v-t graph. 9) If graphs are not given, plot v-t graph when acceleration has constant values in different time intervals. If acceleration varies with time, plot at graph. 10) If quantities other than those which can be obtained directly from the graphs using areas and slopes are required, find equation of the given curve. Then use basic definitions for the functions and either differentiate or integrate the functions. Solved Examples for Understanding Example 9.1.42 For particle moving in a straight line, vt diagram is as shown in Fig. 9.1.26. If x = 10 m at = 10 m at t = 2 s, draw corresponding x-t and a-t diagrams. What is the displacement taking place from t = 6s to t = 10 s? What is the total distance travelled in 10 s ? Solution: Acceleration a = Slope of v-t graph From t = 0 to t = 4 s Area under v-t graph gives displacement (Note that v = 10 m/s at t = 2 s by similarity of triangles) By similarity of the two triangles between t = 6s and t = 10 s, the base of each triangle is 2 s. The a-t and x-t graphs are shown in Fig. 9.1.26 (a). The x-t graph is a parabola with increasing slope of tangent (i.e. anticlockwise rotation of tangent) from t = 0 to t = 4 s as velocity is increasing. From t = 4 s to t = 8 s, x-t graph is a straight line. From t = 6 s to t = 10 s x-t graph is a parabola with decreasing slope as velocity decreases. The curve has a maximum at t = 8 s as v = 0. The total distance travelled can be obtained by adding magnitudes of all areas on v-t graph. ⸫ Distance travelled Example 9.1.43 A car starts from rest with acceleration a = 4 − 0.75 t. When it reaches maximum velocity, it travels with same constant velocity till it has gone a total distance of 200 m. Draw a-t and v-t diagrams for this motion. Hence or otherwise calculate time required by car to go 100 m from starting point. Solution: Given a = 4 - 0.75 t ⸫ At t = 0, a = 4 m/s2 and a = 0 at t = 4 / 0.75 = 5.333 s The a-t graph is a straight line as shown in Fig. 9.1.27. The velocity is maximum when a = 0. As velocity remains constant after reaching maximum value, a = 0 after t = 5.333 s. Change in velocity = Area under a-t graph. v0 = 0 ⸫ v5.333 = 10.667 m/s The v - t graph will be a parabola upto t =5.333 s with tangent rotating clockwise as acceleration is decreasing. Distance travelled can be obtained from a-t graph using x1 = x0 + v0t1 + Moment of area about t1 Here x0 = 0 and v0 = 0 Distance travelled at t = 5.333 ⸫ x5.333 = 37.92 m. ⸫ Time required to travel 100 m and 200 m will be greater than 5.333 s Let t1 = Time to travel 100 m Let t2 = Time to travel 200 m Example 9.1.44 A bus starts from rest from point A and accelerates at 0.8m/s2 till it reaches maximum velocity 12 m/s. After sometime, brakes are applied so that it comes to stop at point B, which is 42 m beyond the point where brakes were applied. Knowing that acceleration is uniform and total travel time is 36 seconds, find distance between the points A and B with help of v-t diagram. Also draw s-t diagram. Solution: The v-t diagram for the motion is shown in Fig. 9.1.28. Slope = 0.8 = 12/t1 ⸫ t1 = 15 s ⸫ A1 = ½ (15) (12) A1 = 90 m A1 is the distance travelled during acceleration. Distance travelled during deceleration = A3 = 42 m ⸫ ½ (t3) (12) = 42 ⸫ t3 = 7 s t1 + t2 + t3 = 36 s 15 + t2 +7 = 36 t2 = 14 s ⸫ A2 = 14 × 12 A2 = 168 m The position co-ordinates are s0 = 0 s15 = 90 m s29 = 90 + 168 = 258 m s36 = 90 + 168 + 42 = 300 m Distance between A and B = 300 m The s-t graph is shown in Fig. 9.1.28 (a). Example 9.1.45 In order to maintain passenger comfort acceleration of an elevator is limited to ± 1.5 m/s2 and jerk (rate of change of acceleration with time) is limited to ± 0.5m/s2 per second. If elevator starts from rest, find - a) Shortest time required to attain a constant velocity 8 m/s. b) Distance travelled in that time. Solution: As the acceleration is variable, we plot the a-t graph as shown in Fig. 9.1.29. Slope = 0.5 = 1.5/t1 ⸫ t1 = 3 s Similarly, t3 - t2 = 3 s ⸫ t3 = 3 + t2 Change in velocity = Area under a-t graph This is the shortest time to attain velocity of 8 m/s. The distance travelled can be obtained using x3 = x0 + v0t3 + Moment of area about t3 Example 9.1.46 A freight elevator F moving upward with constant velocity 5 m/s passes a passenger elevator P which is stopped. Three seconds later, P starts up with acceleration 1.25 m/s2. When P reaches maximum velocity 10 m/s, it maintains that velocity. Draw v-t and y-t curves for these motions. Hence or otherwise, find time and distance required by P to overtake F. Refer Fig. 9.1.30. Solution: The v-t graph for the two elevators is shown in Fig. 9.1.30 (a). The graph for freight elevator starts at t=0 whereas the graph for passenger elevator starts at t = 3 s. When passenger elevator overtakes the freight elevator, the distance travelled by both is same. The y-t graph is straight line for F. The graph is parabola for P from t = 3 s to t = 11 s and then straight line as shown in Fig. 9.1.30 (b). At t = 11 s, for P y11 = 1/2 (8) (10) = 40 m Examples for Practice Q.1 A local train starts from rest from station A and comes to stop at the next station B 4.5 km away in 5 minutes. Maximum velocity is 4/3 times the average velocity and acceleration is twice the retardation. Draw v-t graph for the motion. Find the time of constant maximum velocity and the distance travelled during acceleration. [Ans. : 150 s, 500 m] Q.2 Two stations P and Q are 52 km apart. A train starts from rest from P and accelerates uniformly to attain a speed of 54 km/h in 30 seconds. The speed is maintained until brakes are applied. The train comes to rest at Q with uniform deceleration of 1 m/s2. Determine the total time required to cover the distance between the two stations. [Ans. : 58 min, 9 seconds] • When objects are connected to each other by inextensible cords wrapped around pulleys, the positions, velocities and accelerations of the objects are related. • The equations relating these quantities can be obtained by choosing a reference point or a reference line and specifying the co-ordinates of the connected objects as xA, xB.. etc. • The total length 'l' of cable is then written in terms of these variables. • This equation is differentiated with respect to time to obtain an equation relating velocities. This equation is again differentiated with respect to time to obtain equation relating accelerations. • The sign convention for velocities and accelerations have to be chosen with reference to the chosen origin. For uniformity, we will take the direction towards the chosen origin as positive and away from origin as negative. • The constant length including the length wrapped on the pulleys can be neglected as their derivatives will be zero and they will not affect the equations relating velocities and accelerations. • Consider blocks A and B as shown in Fig. 9.1.31. The fixed pulley is chosen as origin and from this origin, xА and xB are used to specify the positions of A and B respectively. The position of A depends on position of the movable pulley. • The total length 'l' of the cable can be written as d + 2xA + xB = l Differentiating w.r.t. 't', we get • Note that constant distance 'd' does not appear in this equation. Differentiating again w.r.t. t we get, • Thus the velocity and acceleration of 'B' are given by vB = - 2vA and aB = -2aA • If A moves downwards, then its velocity will be considered negative as it is away from origin. Then vB will become positive i.e. towards origin. Hence B will move towards left. • Note that in this case positive sign for velocity of B will indicate direction towards left whereas in kinematical equations the sign convention would be positive towards right. • In the same way, acceleration 'B' can be obtained if acceleration of 'A' is known. • Consider an example in which a motor is used to draw in the cable as shown in Fig. 9.1.32. • In such a case, consider the length of cable on the motor as xA. Then, xA + 2xB = l vA + 2vB = 0 and аA + 2аB = 0 • Here vA and aA represent the velocity and acceleration with which the cable is pulled inside the motor. • If the cable is pulled in, velocity and acceleration have to be taken negative. If cable is released, they have to be taken positive. • Consider an example as shown in Fig. 9.1.33. There are two cables for which the total length remains constant. • We have to define an additional variable x1 defining position of pulley 1. To obtain relation between vA and vB, eliminate v1 v1 = 2 vB ⸫ vA + 2 (2 vB) = 0 vA = - 4 vB Similarly, aA = -4 aB • Once the equations relating the variables are obtained, we can use methods discussed in previous articles for further analysis depending upon whether acceleration is constant or variable. Solved Examples for Understanding Example 9.1.47 Block B starts from rest and moves downward with a stant acceleration. Knowing that after slider block A has moved 400 mm, its velocity is 4 m/s, determine a) acceleration of blocks A and B, b) the velocity and change in position of block B after 2s. Refer Fig. 9.1.34. Solution: Choose distances xA and xB as shown in Fig. 9.1.34 (a). xA + 3xB = l vA + 3vB = 0 …..(1) аA + 3аB = 0 …..(2) vB = 0, аB = Constant↓ As uB = 0, uA = 0 from equation (1) Substituting in equation (2), 20 + 3aB = 0 Example 9.1.48 The motor at C and the motor at D draw the cable with a constant velocity of 4 m/s and a constant acceleration of 8m/s2 respectively. When h = 3 m, the motor at D is switched on. Find the time needed for h = 0, ie, when crates A and B will be at the same level. Refer Fig. 9.1.35. Solution : Let xC and xD be the lengths of the cable on the motors. Choose xA and xB as shown in Fig. 9.1.35 (a). 2xA + xC = l1 Differentiating w.r.t. 't', 2vA + vC = 0 Motor C draws in the cable with constant velocity of 4 m/s. Differentiating twice w.r.t. 't', Examples for Practice Q.1 Block B shown in Fig. 9.1.36 starts from rest and moves downwards with constant accleration. If it attains a velocity of 4 m/s in 5 seconds, determine i) Acceleration of A and B ii) Distance travelled by A after 3 seconds [Ans. : aA = 1.6 m/s2, aB = 0.8 m/s2↓ 7.2 m →] Q.2 Block A shown in Fig. 9.1.37 starts from rest and moves down with constant acceleration. If the velocity of A is 2 m/s after it has moved 4 m, determine i) Accelerations of A and B ii) The velocity of B after 6 s. [Ans. : aA = 0.5 m/s2↓, aB = 0.167 m/s2 ↑ ii) 1 m/s] • In all the previous articles of this chapter, the particle motion was described with respect to a fixed frame of reference. • Generally the earth is taken as a fixed frame of reference for most of the problems. • For example, when we say that the velocity of car moving on a road is 40 km/h towards east, it is with respect to the earth. The motion of the earth in such a case is neglected. • It is important to note that the observer also is at a fixed position with respect to the earth in such a case. • For an observer who is in space, the velocity of the car will not be 40 km/h as such an observer will observe the car to be moving on the earth which itself is moving. • In such cases, the problem is simplified by describing the motion of car with respect to the earth (a moving frame) and then, knowing the motion of earth with respect to the observer, one can find motion of the car with respect to the observer. • In this article, we will consider reference frames having only translation. • Consider two observers A and B having translational motion with respect to a fixed observer O. The position vectors of A and B with respect to O are • The position of B with respect to A or relative to A or as observed by A is denoted by • Using triangle law for addition of vectors, General Procedure for Solving Problems i). To calculate relative velocity, write velocity vectors To calculate relative acceleration, write acceleration vectors ii) To find shortest distance a) Find relative velocity b) Plot initial positions of A and B. c) If d) Draw perpendicular from B on the direction of iii) If A has to meet B or A has to hit B, the shortest distance between A and B must be zero. Then the relative velocity will be along the line joining A and B. iv) In some cases, the velocity of an object is affected by some factors. In such cases, we have to use resultant velocity. For example, if a man tries to row his boat in a river in which water is flowing the velocity of water affects the velocity of boat. The observed velocity of boat Solved Examples for Understanding Example 9.1.49 Two ships leave a port at the same time. The first moves in North-West direction at 50 km/hr and second at 35° South of West at 40 km/hr. Find the relative velocity of second ship with respect to first. Also find distance between them after 25 minutes. After what interval of time will they be 40 km part? Solution: The velocities of the two ships are shown in Fig. 9.1.40. The distance between 1 and 2 can obtained using Example 9.1.50 A man can row a boat at speed 0.22 m/s in still water. He wants to cross 100 m wide river and reach a point exactly opposite to the starting point on the other bank of river. Find direction in which boat must be headed if speed of water current is 0.12 m/s. How long will it take for the man to reach the other bank? Solution: Example 9.1.51 Two collars A and B and block C are connected to each other by a string as shown in Fig. 9.1.42. The system starts from rest and moves with following upward accelerations : aA = 160 mm/s2 aB = 100 mm/s2. Determine relative pelocity of block C with respect to collar A after 4 seconds. Solution: As the two collars A and B and block C, all are moving, we can define positions of B and C with respect to A as shown in Fig. 9.1.42 (a). The total length of cable is Differentiating twice w.r.t. 't', we get Example 9.1.52 Two roads (N-S and E-W) cross at right angles at an intersection as shown in Fig. 9.1.43. Car A is travelling east at constant speed 36 km/h while car B, initially 35 m from intersection starts from rest and travels south at an acceleration 1.2 m/s2 (uniform). Find position, velocity and acceleration of car B relative to car A six seconds after car A just crosses the intersection. Solution: At t = 0, car A is at the intersection and B is 35 m behind the intersection. At t = 6 s, ⸫ At t = 6 m, distance of B from the intersection will be 35 - 21.6 = 13.4 m The position vectors of A and B at t = 6 can be written, taking the intersection as origin, as : Position of B with respect to A is ⸫ Position of B w.r.t. A is Example 9.1.53 As observed from a ship moving due east at 9 km/h, the wind appears to blow from south. After the ship has changed its course and is moving now due north at 6 km/h wind appears to blow from south-west. Assuming that wind has same direction and magnitude of its velocity, find its magnitude and direction. Solution : When ship moves at 6 km/h towards north, the wind appears to come from south- west as shown in Fig. 9.1.44 (c). Examples for Practice Q.1 Two cars A and B are moving on two mutually perpendicular roads as shown in Fig. 9.1.45 with constant velocities vA = 40 km/h and vB = 60 km/h respectively. When A is at the intersection, B is 100 m behind the intersection. Determine i) vA/B ii) Shortest distance between the two cars and the corresponding time. Q.2 A man can row a boat at a speed of 10 km/h in still water. Find the direction in which he should row his boat in river with water flowing at 3 km/h so that he can reach a point exactly oppoiste to the starting point on the opposite bank. If width of river is 250 m find the time required to reach the opposite bank. [Ans. : At an angle of 72.54° with the stream in opposite direction, 94.35 s]1. Variables in Rectilinear Kinematics






2. Variable Acceleration

 • While solving problems, the following concepts will be useful:
• While solving problems, the following concepts will be useful:Solved Examples for Understanding














 where a and x are expressed in m/s2 and m respectively and K is a constant. If velocity of the particle is v = 10 m/s when x = 20 m, determine the value of K and the maximum velocity.
where a and x are expressed in m/s2 and m respectively and K is a constant. If velocity of the particle is v = 10 m/s when x = 20 m, determine the value of K and the maximum velocity.




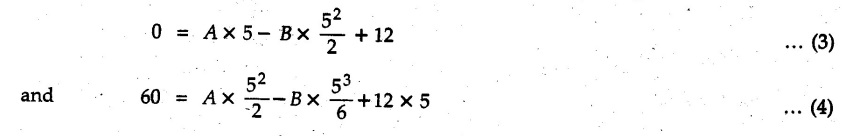

















 + 8t]
+ 8t]3. Motion with Constant Acceleration



























































4. Motion Diagrams











 which represents a cubic curve.
which represents a cubic curve.
























5. Dependent Motion














6. Relative Motion
 respectively which are shown in Fig. 9.1.38.
respectively which are shown in Fig. 9.1.38.
 and is directed from A to B as shown in Fig. 9.1.38.
and is directed from A to B as shown in Fig. 9.1.38. 
 in terms of unit vectors
in terms of unit vectors  Use equation (9.1.12) or (9.1.14).
Use equation (9.1.12) or (9.1.14). in terms of
in terms of  Then use equation (9.1.13) or (9.1.15).
Then use equation (9.1.13) or (9.1.15). in magnitude and direction.
in magnitude and direction. has been calculated in (a), then B is the observer and hence is treated stationary. We plot the motion of A as observed by B which is represented by
has been calculated in (a), then B is the observer and hence is treated stationary. We plot the motion of A as observed by B which is represented by ![]() Plot the direction of A as observed by B in proper quadrant. (It is the direction of
Plot the direction of A as observed by B in proper quadrant. (It is the direction of  ).
). and calculate this perpendicular distance which is the shortest distance using basic trigonometry.
and calculate this perpendicular distance which is the shortest distance using basic trigonometry. for a fixed observer will be resultant of the boat velocity
for a fixed observer will be resultant of the boat velocity  and water velocity
and water velocity  as shown in Fig. 9,1,39.
as shown in Fig. 9,1,39.














Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : with Solved Example Problems - Kinematics - Rectilinear Motion
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
