kinematic chain

KINEMATIC CHAIN

• A kinematic chain is defined as the combination of kinematic pairs in which each link forms a part of two kinematic pairs and the relative motion between the links is either completely constrained or successfully constrained.

• A chain may be locked, constrained and unconstrained.

• A kinematie chain having four links is known as a simple kinematic chain and a kinematic chain having more than four links is known as a compound kinematic chain.

• Closed and open kinematic chain:

■ When links are connected in a sequence, with first link connected to the last (forming a closed loop), then the chain is called as closed kinematic chain.

■ When links are connected in a sequence, with first link not connected to the last (forming an open loop), then the chain is called as open kinematic chain.

1. Conditions to form a Kinematic Chain

• The required equations/conditions to form a kinematic chain are:

where

n = Number of links,

p = Number of pairs,

j = Number of binary joints, and

h = Number of higher pairs.

• If above equations are satisfied, then the assemblage of links form a kinematic chain.

• The equations (1.1) and (1.2) can be applied only for kinematic chains having lower pairs, whereas the equation (1.3) can be applied for kinematic chains having lower and/or higher pairs.

• It may be noted that when h = 0 (i.e., no higher pair, only lower pairs) in-équation (1.3),  we get j = 3/2 n − 2, which is exactly the same as that of equation (1.2).

2. A.W. Klien's Criterion of Constraint to Determine Nature of Chain

• A.W. Klien's criterion of constraint is used to determine the nature of chain, i.e., whether the chain is a locked chain (i.e., structure) or a constrained chain or an unconstrained chain.

• According to A. W. Klien's criterion of constraint, in equation (1.3) [or in equations (1.1) and (1.2)],

(i) If L.H.S > R.H.S., then the given chain is called locked chain or structure.

(ii) If L.H.S. = R.H.S., then the given chain is called constrained kinematic chain.

(iii) If L.H.S. < R.H.S., then the given chain is called unconstrained kinematic chain.

Example 1.1

Show that a combination of three links cannot form a kinematic chain.

Solution:

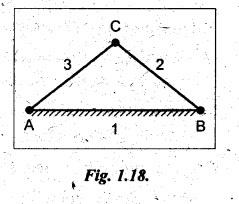
Consider an assemblage of three links AB, BC and CA which are pin jointed at A, B and C, as shown in Fig.1.18.

From Fig.1.18, we can write

Number of links, n = 3.

Number of pairs, p = 3

Number of joints, j = 3

Number of higher pairs, h = 0

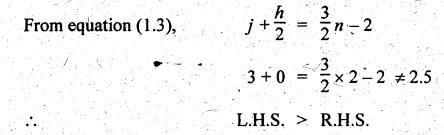
Since L.H.S. > R.H.S., therefore the given three links chain is not a kinematic chain; it is a locked chain or structure. Ans. 

Note

Locked chain forms a rigid frame which is used in bridges and trusses.

Example 1.2

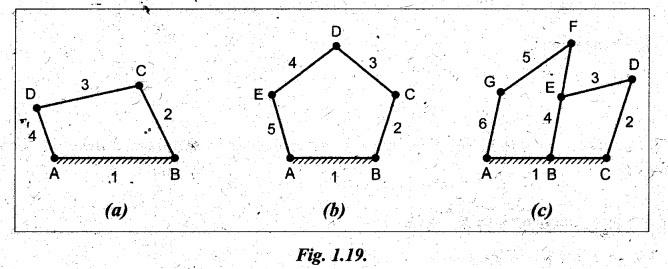
Fig.1.19 shows the chains with four links, five links and six links. Determine whether they are locked, constrained or unconstrained kinematic chain.

Solution:

Case (a): Four link chain

Referring to Fig.1.19(a), we can write

n = 4; p = 4; j = 4; and h = 0.

From equation (1,3),

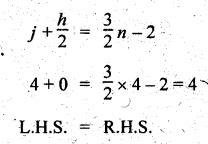
Since L.H.S.= R.H.S., therefore the four-bar chain is a constrained kinematic chain. Ans. 

Case (b): Five link chain

Referring to Fig.1.19(b), we can write

n = 5; p = 5; j = 5; and h = 0.

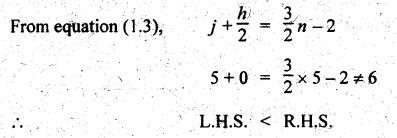
Since L.H.S. < R.H.S., therefore the five bar chain is an unconstrained kinematic chain. Ans.  

Case (c): Six link chain

Referring to Fig.1.19(c), we can write

n = 6; p = 5; j = 7; and h = 0.

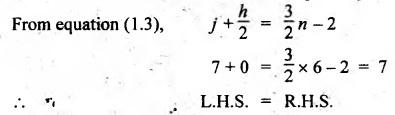
Since L.H.S. = R.H.S., therefore the six bar chain is a constrained kinematic chain. Ans.