Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Joule-Thomson Coefficient
Definition, Formula, Equation, Experiment, Curve diagram | Thermodynamics
The Joule-Kelvin effect or Joule-Thomson effect is an efficient way of cooling gases.
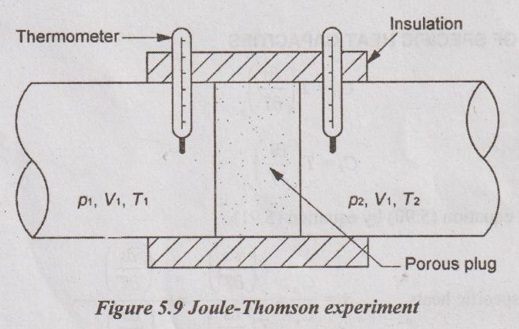
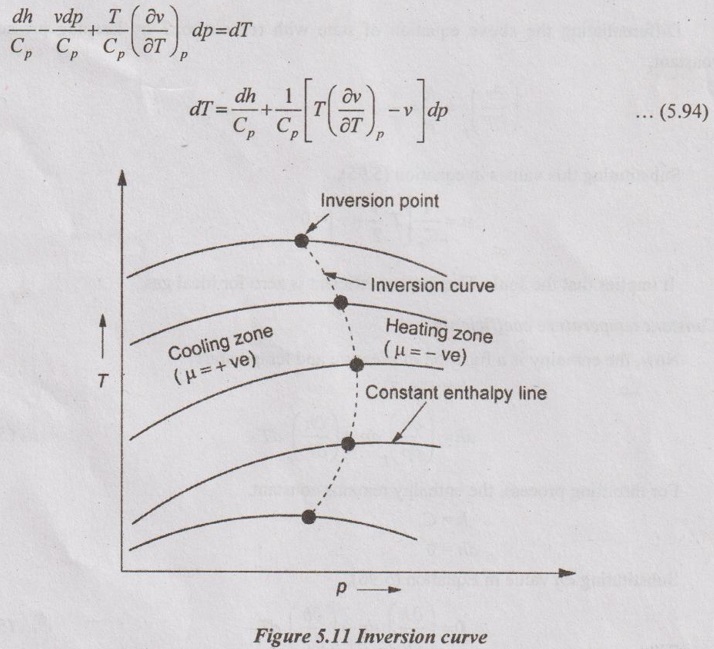
JOULE-THOMSON COEFFICIENT The Joule-Kelvin effect or Joule-Thomson effect is an efficient way of cooling gases. In this process, a gas is made to undergo a continuous throttling process. A constant pressure is maintained at one side of a porous plug and a constant low pressure is maintained at the other side. The apparatus is thermally insulated so that the heat loss can be neglected. Joule-Thomson coefficient is defined as the ratio of change in temperature to change in pressure at constant enthalpy. It is denoted by (μ). Throttling process is defined as the fluid expansion through a minute orifice or slightly opened valve. During throttling process, both pressure and velocity are reduced. But there is no heat transfer and no work done by the system. In this process, the enthalpy remains constant. The internal energy of an ideal gas and an incompressible substance is a function of temperature only, u = u(T). Initially, one tank contains air at high pressure and the other tank is evacuated. When the thermal equilibrium attains, the valve is opened to allow air to pass from one tank to the other until the pressures are equalized. The bulbs were immersed in a well-stirred water bath equipped with a sensitive thermometer. It is observed that there is no change in temperature of the water bath and understood that no heat was transferred to or from the air. Then, it is concluded that there is no change in volume and pressure due to no work done. So, it is proved, the internal energy is a function of temperature only and not a function of pressure or specific volume. Figure 5.9 shows the arrangement of porous plug experiment. In this experiment, a stream of gas at a pressure p1 and temperature T1 is continuously allowed to flow through a porous plug. The gas comes out from the other side of the porous plug at a pressure p2 and temperature T2. The whole apparatus is completely insulated. Therefore, no heat transfer takes place. Also, the system does not exchange work with the surrounding. Therefore, Q = 0 and W = 0 From Steady Flow Energy Equation (SFEE), Since there is no considerable change velocity, v1 = v2 and z1 = z2. Q = 0, W = 0, v1 = v2 and z1 = z2 are applied in SFEE. So, the equation (5.93) becomes h1 = h2 Enthalpy at inlet, h1 = Enthalpy at outlet, h2 It indicates that the enthalpy is constant for throttling process. It is assumed that a series of experiments performed on a real gas by keeping the initial pressure p1 and temperature T1 constant with various reduced down steam pressures (p2, p3, p4 ...). So, the downstream temperature also changes. The results from these experiments can be plotted as a constant enthalpy curve on T-p (Temperature - Pressure) plane. The slope of a constant enthalpy is known as Joule-Thomson coefficient, it is denoted by μ. For real gas, μ may be either positive or negative depending upon the thermodynamic state of the gas. Case (i): There is always a pressure drop in throttling process. So, Δp and temperature change are negative. Therefore, μ will be positive. This throttling process produces the cooling effect since the temperature reduces. Case (ii): There is always a pressure drop in throttling process. So, Δp is negative. When the temperature change is positive, μ is negative. This throttling process produces the heating effect since the temperature increases. Case (iii): When μ is zero, the temperature of the gas will remain constant with throttling process. The temperature at which μ = 0 is called inversion temperature for a given pressure. The maximum point on each curve is called inversion point and the locus of the inversion point is called inversion curve as shown in Figure 5.11. A generalized equation of the Joule-Thomson coefficient can be derived by using the change of enthalpy equation. We know that Dividing the equation by Cp on both sides, Differentiating this equation with respect to pressure at constant enthalpy, From equation (5.95), the Joule-Thomson coefficient (μ) is determined in terms of measurable properties such as pressure (p), temperature (T), specific volume (v) and Cp. We know that the equation of state for ideal gas is given by pv = RT Engineering Thermodynamics Differentiating the above equation of state with respect to T by keeping pressure, p constant, Substituting this values in equation (5.95), It implies that the Joule-Thomson coefficient is zero for ideal gas. Now, the enthalpy is a function of pressure and temperature. For throttling process, the enthalpy remains constant. h = C dh = 0 Substituting dh value in Equation (5.96), Throttling process:
Throttling process:Joule-Thomson experiment:
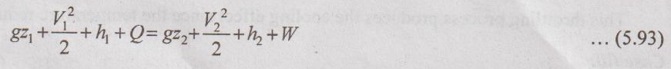
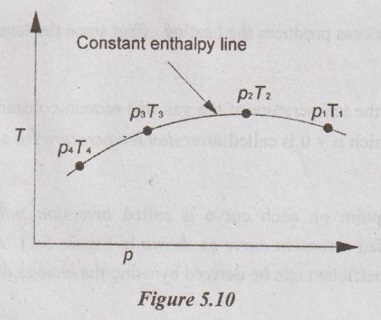
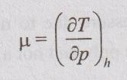
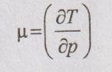
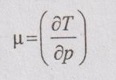
Inversion curve:
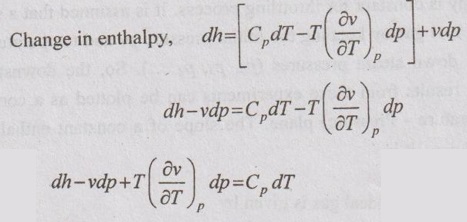
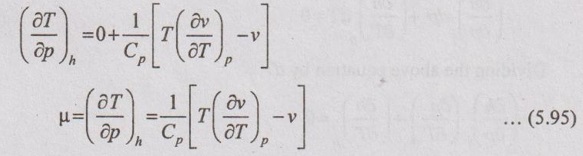
Joule-Thomson coefficient for ideal gas:
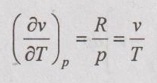
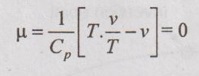
Constant temperature coefficient:
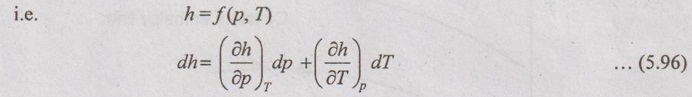

Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : Definition, Formula, Equation, Experiment, Curve diagram | Thermodynamics - Joule-Thomson Coefficient
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
