Matrices and Calculus: Unit III: Functions of Several Variables
Jacobians
Definition, Properties, Worked Examples, Exercise with Answers
Jacobians have many important applications such as functional dependence, transformation of variable in multiple integrals, problems in partial differentiation and in the study of existence of implicit functions determined by a system of functional equations.
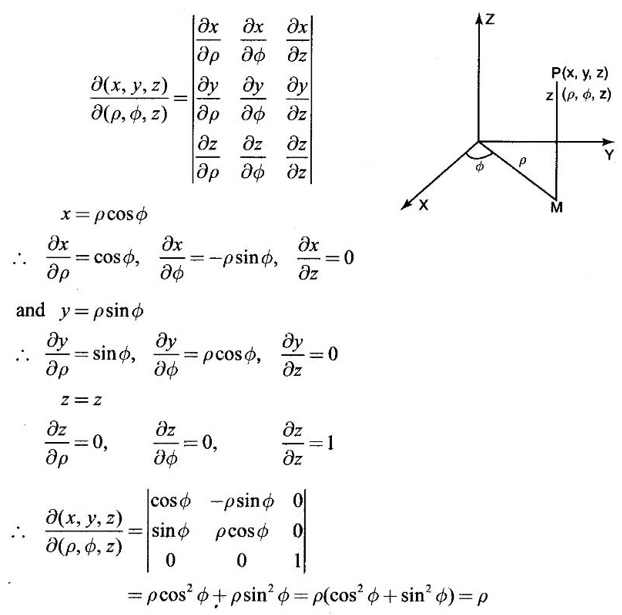
JACOBIANS Jacobians have many important applications such as functional dependence, transformation of variable in multiple integrals, problems in partial differentiation and in the study of existence of implicit functions determined by a system of functional equations. Definition 3.3.1 (1) If u and v are continuous functions of two independent variables x and y, having first order partial derivatives, then the determinant (2) If u, v, w are continuous functions of three independent variables x, y, z having first order partial derivatives then the Jacobian of u, v, w with respect to x, y, z is defined as Similarly, we can define Jacobians for functions of 4 or more variables. For simplicity we shall prove the properties of Jacobians for two variables. However, they can be extended to any number of variables. Property 1: If u and v are functions of x and y, then Proof Let u = f1(x, y) and v = f2(x, y) be continuous functions of two independent variables x and y having first order partial derivatives then The condition for these equations to be solvable for x and y is J ≠ 0. Since u and v are independent variables from differentials (1) and (2) we get Property 2: Jacobians of composite functions or chain rule If u and v are functions of p and q, where p and q are functions of x and y, then Proof If u and v are continuous functions of p and q and p and q are functions of x and y, then Property 3: If u and v are functions of two independent variables x and y and u and v are functionally dependent Proof If u and v are not independent, then there is a relation between u and v. Let f(u, v) = 0 be the relation between u and v. Differentiating with respect to x and y we have, Note (1) The converse of property 3 is also true. (2) The property can be extended to functions of more than two variables. Property 4: If x = f(u, v), y = g(u, v) and h(x, y) = F(u, v) then Example 1 Solution and v = y2 – 2 Example 2 Solution Example 3 If x = r cos θ, y = r sin θ, then find the Jacobian of x and y with respect to r and θ. Solution The Jacobian of x and y with respect to r and θ is Note x = r cos θ, y = r sin θ transforms cartesian coordinates into polar coordinates. Example 4 Solution Since x and y are function of u, v we can find Subtracting in (1), we get Example 5 If x = u (1 − v), y = uv, then compute J and J' and prove that JJ' = 1. Solution We know J = To prove JJ' = 1 Given x = u(1 − v) We have to find u and v in terms of x and y. x = u (1 − v) = u - uv and y = uv ⇒ x = u - y Example 6 If u = 2xy, v = x2 - y2, x = r cos θ, y = r sin θ, evaluate Solution Given u, v are functions of x and y and x and y are functions of r and θ. So by property 2 of composite function Since x = r cos θ, y = r sin θ ⇒ x2 + y2 = r2 cos2 θ + r2 sin2 θ = r2 From example 3, we have Example 7 For the transformation x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ, compute the Jacobian of x, y, z with respect to r, θ, φ. Solution The Jacobian of transformation Note This is the transformation of cartesian coordinates to spherical polar coordinates (r, θ, φ) Example 8 Solution We have Note This is the transformation of cartesian coordinate to cylindrical coordinates (ρ, φ, z). Example 9 Solution = −1(+1−1)−1(− 1 − 1) +1(1+1) = 0 + 2 + 2 = 4 Example 10 If u = x + y + z, uv = y + z, uvw = z, then find Solution Given u = x + y + z, uv = y + z, uvw = z Example 11 Solution Example 12 Solution Example 13 Solution If y1, y2 y3,... yn are implicitly given as functions of x1, x2, ..., xn by the functional equations f1(x1, x2, ..., xn, y1, y2 y3,... yn) = 0 for i = 1, 2, ... n, then Example 14 If F = xu + v - y, G = u2 + vy + w, H = zu – v + vw compute (1) Solution F = xu + v - y, G = u2 + vy + w H = zu – v + vw These equations implicitly define x, y, z in terms of u, v, w. ⸫ by the Jacobian of implicit functions, we have Example 15 If x + y + z - u = 0, y + z - uv = 0, z – uvw = 0 then find Solution Given x + y + z - u = 0, y + z - uv = 0, z - uvw = 0 These equations implicitly define x, y, z interms of u, v, w Let f1 = x + y + z - u f2 = y + z - uv f3 = z - uvw By the Jacobian of implicit functions Given f1 = x + y + z - u f3 = z - uvw
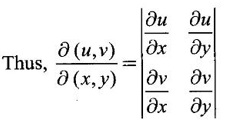
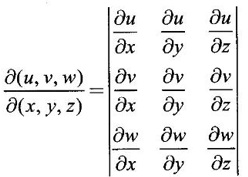
1. Properties of Jacobians

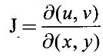



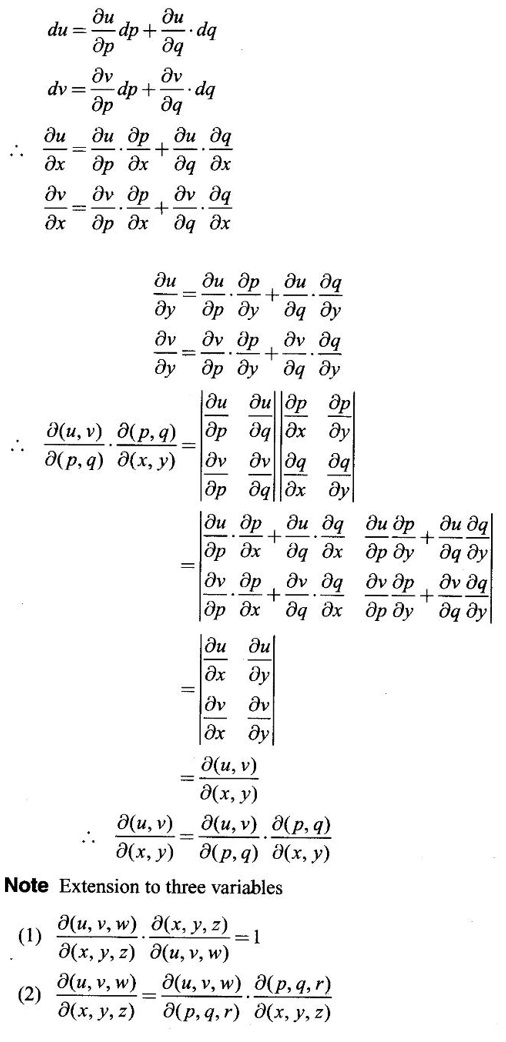
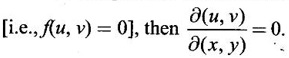
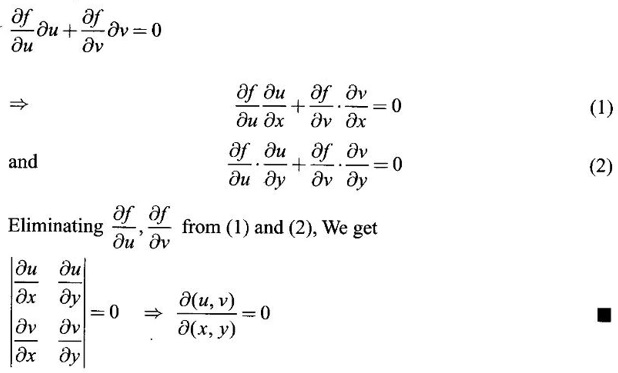
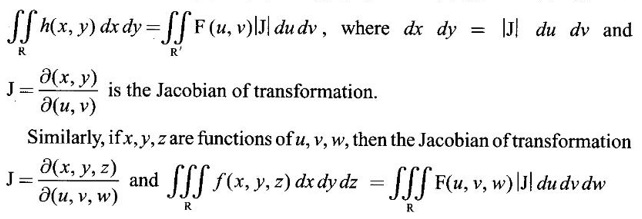
WORKED EXAMPLES


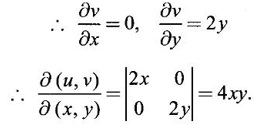
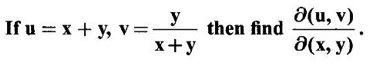

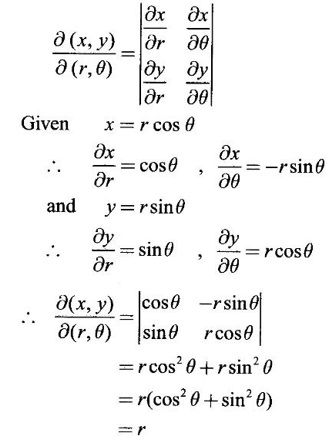




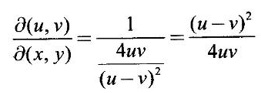
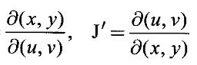
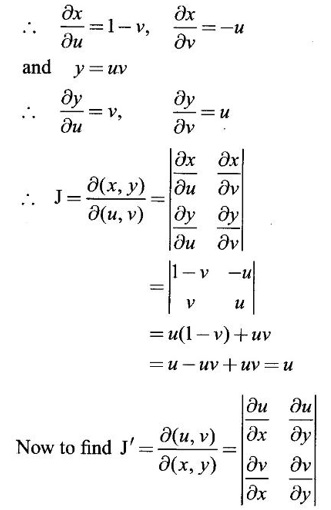

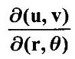 without actual substitution.
without actual substitution.
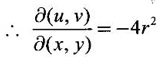


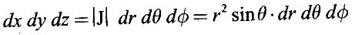




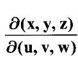





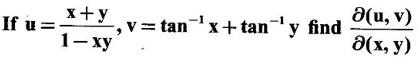

2. Jacobian of implicit functions

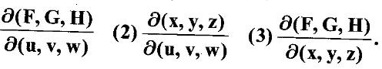


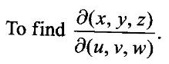


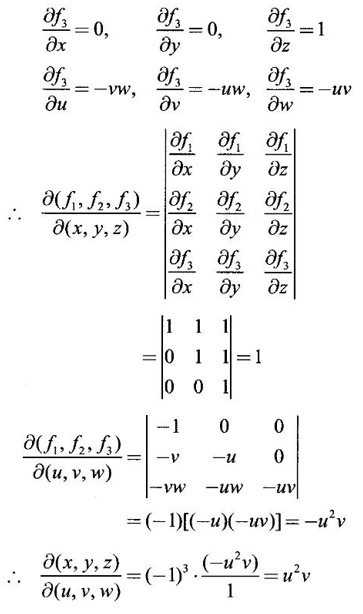
EXERCISE 3.3

ANSWERS TO EXERCISE 3.3.

Matrices and Calculus: Unit III: Functions of Several Variables : Tag: : Definition, Properties, Worked Examples, Exercise with Answers - Jacobians
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
