inversions of four-bar chain

INVERSIONS OF FOUR-BAR CHAIN

• From a four-bar chain, four different inversions can be obtained by fixing its four links one at a time in turn. Applying each of the inversions, several useful mechanisms can be obtaind.

• Table 1.4 shows the inversions of four-bar mechanism and their important applications.

Table 1.4. Inversions of four-bar chain

1. First/Second Inversion (Crank-Rocker Mechanism)

• As shown in Fig.1.27(a), link 1 is the crank, link 4 is fixed and link 3 oscillates whereas in Fig.1.27(b), link 2 is fixed and link 3 oscillates. The mechanism thus obtained is known as crank-rocker mechanism or crank-lever mechanism or rotary-oscillating converter.

• Application: Beam engine

Beam Engine

• Beam engine is an example of crank-rocker mechanism, where one link oscillates, while the other rotates about the fixed link, as shown in Fig.1.28.

• When the crank (link 1) rotates, the lever (link 3) oscillates. The oscillatory motion of the lever is converted into reciprocating motion of a plunger in a cylinder as shown in Fig. 1.28.

• Thus this mechanism is used to convert the rotary motion into reciprocating motion.

2. Third Inversion (Double-Crank Mechanism)

• If the shortest link, i.e., link 1 (crank) is fixed, the adjacent links 2 and 4 would make complete revolutions, as shown in Fig.1.29. The mechanism thus obtained is known as crank-crank mechanism or double-crank mechanism or rotary-rotary converter drag link mechanism.

• Application: Coupling of the locomotive wheels.

1. Coupling of Locomotive Wheels

• Coupled wheels of a locomotive is an example of a double-crank mechanism where both cranks rotate about the points in the fixed link. It consists of four links and the opposite links are equal in length, as shown in Fig.1.30.

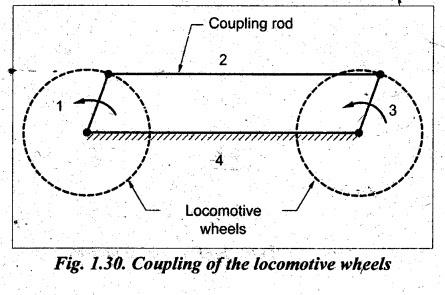
• Since links 1 and 3 work as two cranks, the mechanism is also known as rotary-rotary converter.

• This mechanism is used to transmit rotary motion from one wheel to the other' wheel.

3. Fourth Inversion (Double-Rocker Mechanism)

• If the link opposite to shortest link is fixed, i.e., link 3 is fixed, then the shortest link (link 1) is made coupler and the other two links 2 and 4 would oscillate as shown in Fig.1.31. The mechanism thus obtained is known as rocker-rocker or or double-lever double-rocke mechanism or oscillating-oscillating converter.

• Applications: 1. Watt's indicator mechanism

2. Pantograph

3. Ackermann steering

1. Watt's Indicator Mechanism

• This mechanism was invented by James Watt for his steam engine to guide the piston rod along straight line. It is also known as simplex indicator.

• As shown in Fig.1.32, the Watt's indicator mechanism consists of four links: Link 3 is fixed, link 2 is ABC, link 3 is CDP, and link 1 is BED.

• Links ABC and CDP act as levers and due to this, the mechanism is also known as double-lever or double-rocker mechanism.

• The point E is connected to piston of indicator cylinder and the displacement of point E (and link BED) is directly proportional to the steam or gas pressure in the indicator diagram.

• In Fig.1.32, continuous lines depict the initial position of the mechanism, whereas the dotted lines show the position of the mechanism when steam or gas pressure acts on the indicator piston.

• The point P (of the link CDP) traces the variation of pressure in the cylinder. It may be noted that the point P traces approximately the straight line motion (PP') corresponding to motion of E. For this reason, this mechanism is also known as straight line generator mechanism.

2. Pantograph

Pantograph is a device which is used to reproduce a displacement exactly in an enlarged or reduced scale.

3. Ackermann Steering

The Ackermann steering mechanism is used for changing the direction of the wheel axles with reference to the chasis, so as to move the vehicle in any desired path.