inversions of double slider-crank chain

INVERSIONS OF DOUBLE SLIDER-CRANK CHAIN

The double slider-crank chain provides three different inversions. Table 1.6 shows the inversions of double slider-crank chain and their important applications.

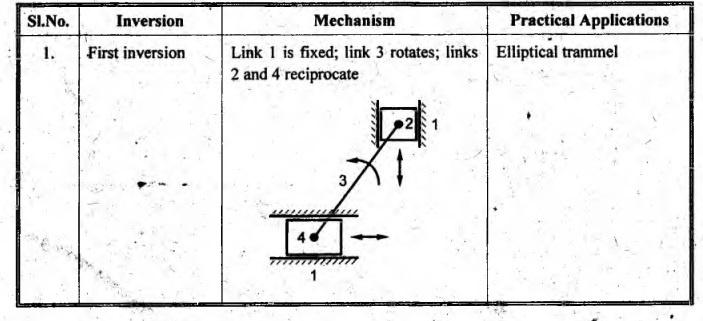
Table 1.6. Inversions of double slider-crank chain and their applications

• By fixing any of the two sliders in the double slider-crank chain only scotch yoke mechanism is obtained. Therefore, only three different mechanisms/inversions are obtained from double slider-crank chain.

1. First Inversion

• First inversion is obtained by fixing the link 1.

• In this, the two adjacent pairs 2-3 and 3-4 are turning pairs and the other two pairs 1-2 and 1-4 are sliding pairs.

• Application: Elliptical trammel

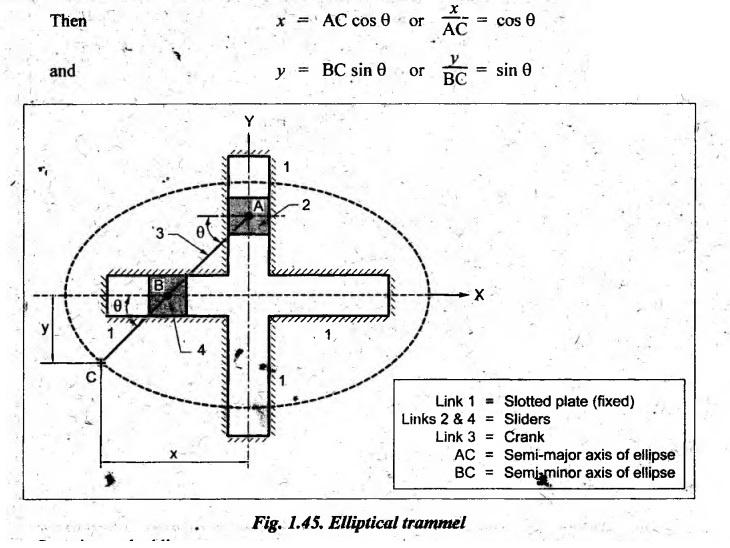
1. Elliptical Trammel

• Elliptical trammel is an instrument used for drawing ellipses.

• This inversion is obtained by fixing the link 1 (i.e., slotted plate), as shown in Fig.1.45. The link 1 or the fixed plate has two straight grooves in it, at right angles to each other.

• When the links 2 and 4 (sliders) slide along their respective grooves, the end C of the extension BC of the link AB, traces an ellipse such that AC and BC are the semi-major and semi-minor axis of the ellipse respectively.

• Proof: Let AC makes an angle θ as shown in Fig.1.45 and co-ordinates of point C be (x, y).

Squaring and adding, we get

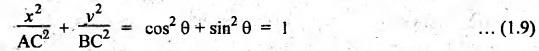
which is the equation of an ellipse.

The above expression proves that AC is the semi-major axis of the ellipse and BC is the semi-minor axis of the ellipse.

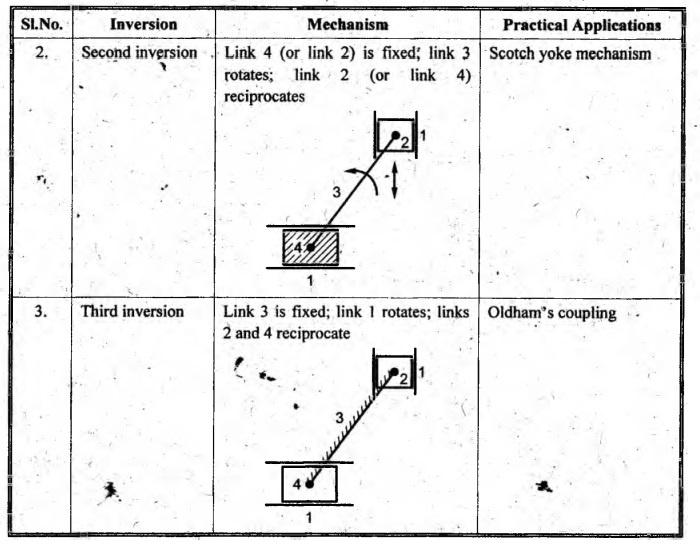
2. Second Inversion

• Second inversion is obtained by fixing any one of the slider blocks (i.e., link 2 or link 4) of the first inversion.

• When link 4 is fixed, end B of crank 3 rotates about A and link 1 reciprocates in the horizontal direction.

• Application: Scotch yoke mechanism

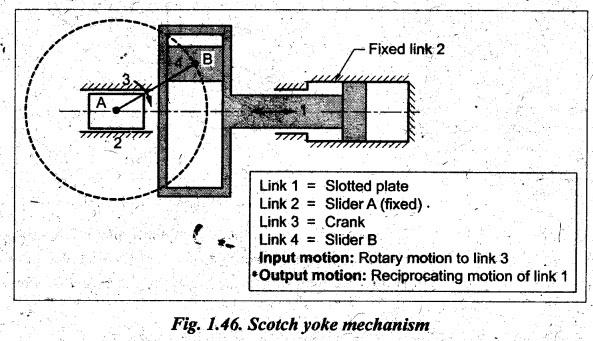
1. Scotch Yoke Mechanism

• This inversion is used for converting rotary motion into reciprocating morton. Nowadays, it is used as sine-cosine generator for computing elements and as a mechanism on a test machine to produce vibrations.

• It is obtained by fixing any one of the sliders (here link 2), as shown in Fig.1.46. As crank 3 rotates about fixed point A, the horizontal portion of link 1 slides or reciprocates in the fixed link 2. The slider B (which is attached to crank) reciprocates. This causes the slotted lever frame (link 1) to reciprocate. The fixed slider A guides the frame to reciprocate. Thus this mechanism converts rotary motion of link 3 into reciprocating motion of link 1.

3. Third inversion

• Third inversion is obtained by fixing the link 3 as shown in Table 1.6.

• When link 3 iş fixed, link I rotates and links 2 and 4 reciprocate.

• Application: Oldham's coupling.

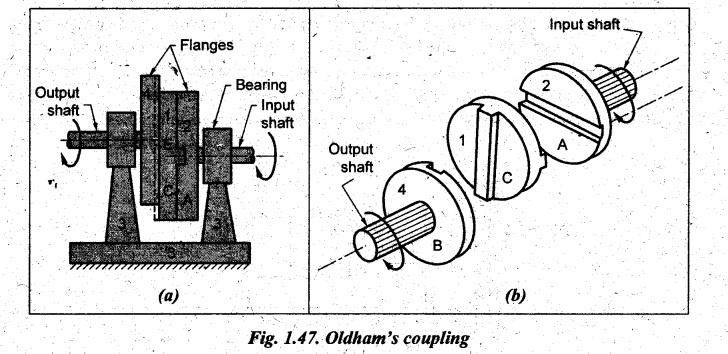
1. Oldham's Coupling

• The Oldham's coupling is used for transmitting motion between two shafts when (i) the shafts are parallel, but not coaxial, and (ii) the centre distance between their centre lines is small.

• The shafts are coupled in such a way that if one shaft rotates, the other shaft also rotates at the same speed.

• The inversion is obtained by fixed the link 3 as shown in Fig.1.47.

• It consists of a driving shaft, fitted with a flange (link 2) having a diametrical slot on its face; a driven shaft fitted with flange C (link 4) also has diametrical slot on its face. This whole makes link 4. The slots on the two flanges are at right angles to each other. An intermediate piece circular shape, having tongues X and Y at right angles on opposite sides, is fitted in between the flanges of the two shafts in such a way that the tongues of the intermediate piece get fitted closely in the slots of flanges. The intermediate circular piece E forms link 1 which slides between the flanges C and D.

• When driving shaft rotates through certain angle, the driven shaft also rotates through the same angle. Motion is transmitted through intermediate link 1. If the distance between the axis of the shafts is x, it will be the diameter of a circle traced by the center of intermediate piece.

• The maximum sliding velocity of each tongue along its slot is given by

v_s = r . ω

where

v_s = maximum sliding velocity of each tongue along its slot,

r = Distance between the axis of shafts, and

ω = Angular velocity of the shaft.