Engineering Physics: Unit I: Mechanics
Introduction to non - linear oscillations
Vibration phenomena is well understood by using linear vibrations theory include small amplitude vibrations.
INTRODUCTION TO NON - LINEAR OSCILLATIONS Vibration phenomena is well understood by using linear vibrations theory include small amplitude vibrations. Examples: Vibration of long, slender objects like long bridges, aeroplane wings and helicopter blades, small rocking motions of ships in calm waters; the simplest whirling motions of flexible shafts, and so on. However, interactions between bridges and foundations, between wings / blades and air, between ships and waves, between shafts and bearings, and so on, are all nonlinear. Non - linear systems can show behaviours that linear systems cannot. These include: (a) múltiple steady state solutions, some stable and some unstable, in response to the same inputs. (b) jump phenomena, involving discontinuous and significant changes in the response of the system as some forcing parameter is slowly varied. (c) response at frequencies other than the forcing frequency. (d) internal resonances, involving the different parts of the system vibrating at different frequencies, all with steady amplitudes (the frequencies are usually in rational ratios, such as 1:2, 1:3, 3:5, etc.), (e) self sustained oscillations in the absence of explicit external periodic forcing, and (f) complex, irregular motions that are extremely sensitive to initial conditions (chaos). A linear oscillator can oscillate with only one frequency, its motion is sinusoidal and periodic. If the return force in the spring is not linear, the motion will still repeat itself, but it will no longer have only a single frequency in its motion. The oscillations will repeat over and over, always with the same period, but the position as a function of time will not be given by y = A cos (2 πf1 t), where f1 = 1/P. Here P is period. • In order to describe the motion of the non-linear oscillator, the sine wave different frequencies to be considered. • Non - linear oscillators describe motion that exactly repeats itself cycle after cycle, we need building blocks that oscillate with exactly the same period P, or at least integer fractions of the period, namely P, P /2, P /3, etc., • We can write symbolically as Pn = P /n where n is an integer, n = 1, 2, 3, .... Since the frequency fn is the inverse of the period. The first four harmonics. The fourth harmonic is shown below the others for clarity. The dashed vertical line shows half the period, so t = P/2. Note the difference between the behavior of the odd (1 and 3) harmonics and the even harmonics (2 and 4) just after t = P/2. Thus, the complex motion is resultant of sine waves of several frequencies called harmonics. The sine waves with frequencies that are integer multiples of the lowest frequency f1 = 1/P. They go through exactly 1, 2, etc. complete oscillations in the period P. The frequency f1 is called the fundamental of the harmonic series. The first four harmonics are shown in fig. 1.48, which are given by It is noted that at the midpoint, all of the harmonics are zero, but the even harmonics have gone through an integer number of cycles, and they are going positive again while the odd harmonics have gone through 1/2, 3/2, 5/2, etc cycles, and are going negative. If the period of the oscillation is P, then the frequencies present in the motion are To summarize, the motion contains the frequency f1 which is the inverse of the period, plus harmonics (integer multiples) of this frequency. This is very different from the simple oscillator. In the simple oscillator we had one frequency which only depended on the stiffness and inertia of the system. Now, the motion of the non-linear oscillator consists of a complex motion made up of harmonics of f1. The participation of each harmonic in a complex oscillation depends on the details of the nonlinearity. There are two important characteristics of the nonlinear oscillator. 1. The effects of the nonlinearity becomes much more important as the amplitude is increased. 2. For some types of nonlinearity, the frequency of the oscillator will change with amplitude. Thus when we drive a nonlinear system, the larger the amplitude the more important the higher harmonics are. Non - linear system is a system in which the change of the output is not proportional to change of the input. Non linear problems are of interest to engineers, biologists, physicists, mathematicians and many other scientists because most systems are inherently non- linear in nature.Non - linear oscillators
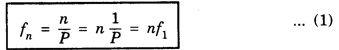

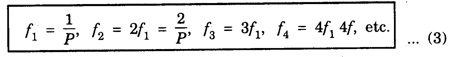
Applications & uses
Engineering Physics: Unit I: Mechanics : Tag: : - Introduction to non - linear oscillations
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
