Matrices and Calculus: Unit IV: Integral Calculus
Integration by Parts
Worked Examples, Exercise with Answers | Integral Calculus
When the integrand can not be reduced to standard form by substitution, we apply integration by parts. It corresponds to product rule in differentiation.
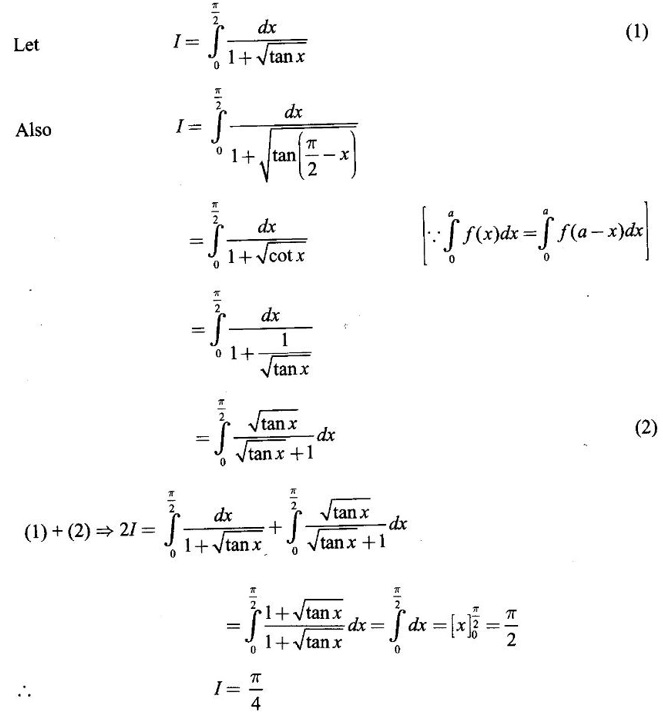
Integration by Parts When the integrand can not be reduced to standard form by substitution, we apply integration by parts. It corresponds to product rule in differentiation. If u and v are functions of x, then Integrating, we get This is called the formula for integration by parts. The success of the method depends on the proper choice of u as that function which comes first in the word 'ILATE' where I - inverse circular function L - logarithmic function A - algebraic function T - trigonometric function E - exponential function Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Evaluate Solution Example 4 Evaluate Solution Example 5 Evaluate Solution Example 6 Find Solution Example 7 Evaluate Solution Example 8 Evaluate Solution Example 9 Evaluate Solution Put t = sin x. Example 10 Evaluate Solution Example 11 Evaluate Solution Example 12 Evaluate Solution Example 13 Using integration by parts, evaluate Solution Repeated application of integration by parts is called Bernoulli formula. If u and v are differentiable functions of x, then where primes denote differentiation and suffixes denote integration. That is and If u is a polynomial in x, then Bernoulli's formula terminates. Solution It is a product of two functions. So, using integration by parts, we evaluate the integral. Solution It is a product of two functions. So, we use integration by parts to evaluate the integral. Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Evaluate Solution Example 4 Evaluate Solution Example 5 Evaluate Example 6 Evaluate Solution Example 7 Evaluate Solution Integrals of type We derive the reduction formula for some standard integrals Example 1 Solution Example 2 Solution Deduction: If n is a non-negative integer, then prove that Solution Case 1: If n is even, then Case 2: if n is odd, then Similarly, we get Example 3 Solution Example 4 Solution Example 5 Show that Solution Example 6 Solution Here n = 5 is odd Example 7 Evaluate Solution Example 8 Evaluate Solution Example 9 Solution Here, n = 7 is odd Evaluate following integrals by integration by parts formula If f(x) is a continuous and integrable function of x in [a, b], then the following properties are satisfied. Note That is the value of a definite integral is unaffected by the change of dummi variable, if the limits and function are the same. Substituting in (1), we get Example 1 Evaluate Solution Example 2 Solution Example 3 If ƒ is continuous on [0, π] show that Solution Example 4 Show that Solution Note Since the right hand side is independent of n, this is true for all n. Example 5 Prove that Solution Example 6 Prove that Solution Example 7 Evaluate Solution Example 8 Prove that Solution Note In the interval (0, π) we cannot put t = tan x as it is not increasing there and discontinuous at x = π/2. So, we reduced the interval from (0, π) to [0, π/2] by property 6, so that in (0, π/2), tan x is strictly increasing. Example 9 Evaluate Solution Example 10 Evaluate Solution Here the interval is [0,4], Example 11 Evaluate Solution Example 12 Evaluate Solution Example 13 Evaluate Solution We know We shall now find derivatives of integrals using part-I of Fundamental theorem of calculus and we obtain Leibnitz rule for derivative. Example 1 If g(x) = Solution Example 2 Solution Example 3 Solution Example 4 Solution Example 5 Solution Example 6 Solution Example 7 Solution Example 8 Solution Example 9 Solution Example 10 The function f is continuous and satisfies Solution Differentiate with respect to x, we get To find c, substitute for f in the given equation f(t) = 2t15 Evaluate the following integrals 6. Definite integral Working Rule Example 1 Show that Solution Example 2 Solution Example 3 Show that Solution Let To convert the product into sum, take logarithm on both sides Example 4 Solution Integrating by parts, we get Evaluate the following limits as integrals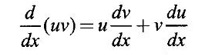
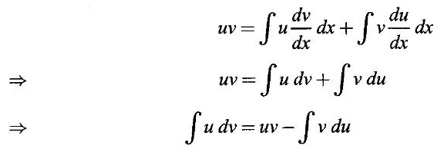
WORKED EXAMPLES



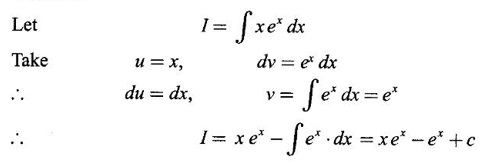
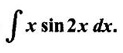

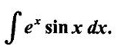

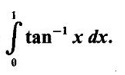
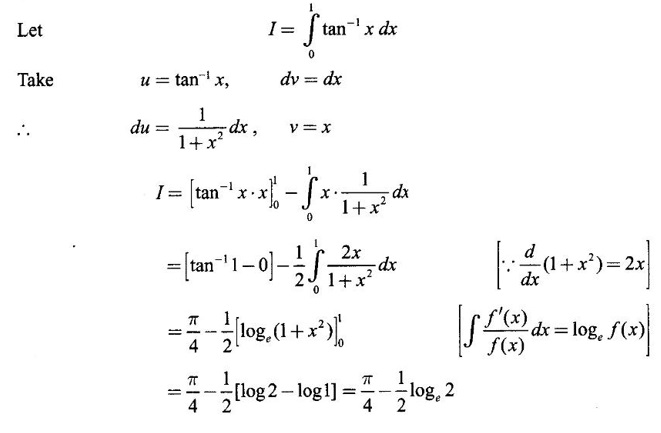


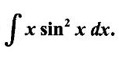
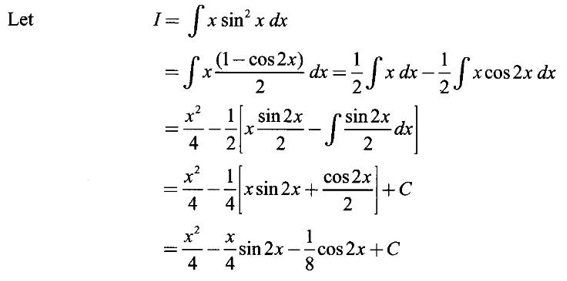

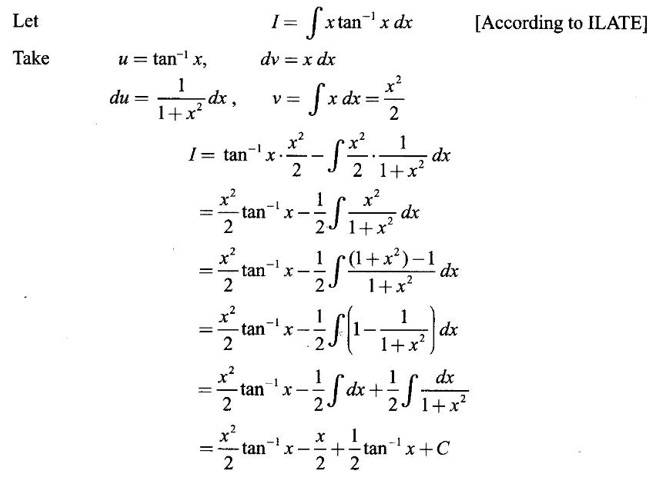


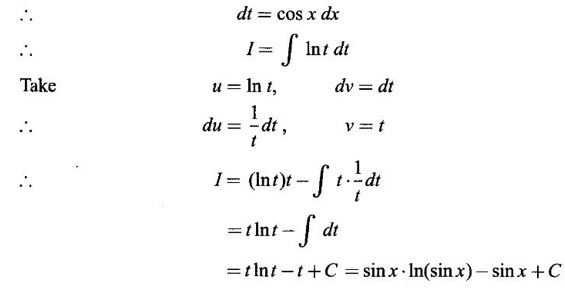
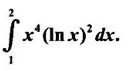


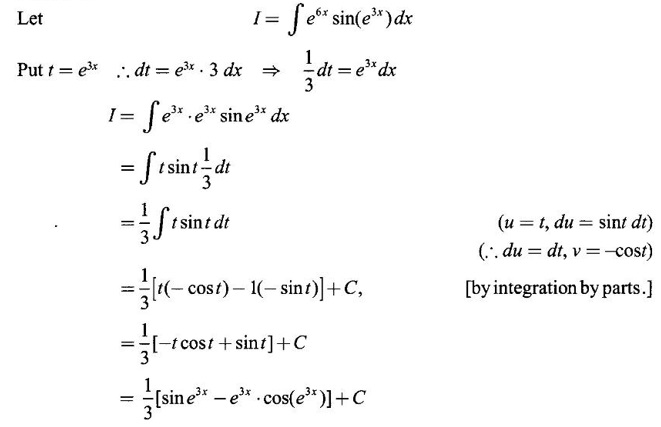
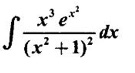
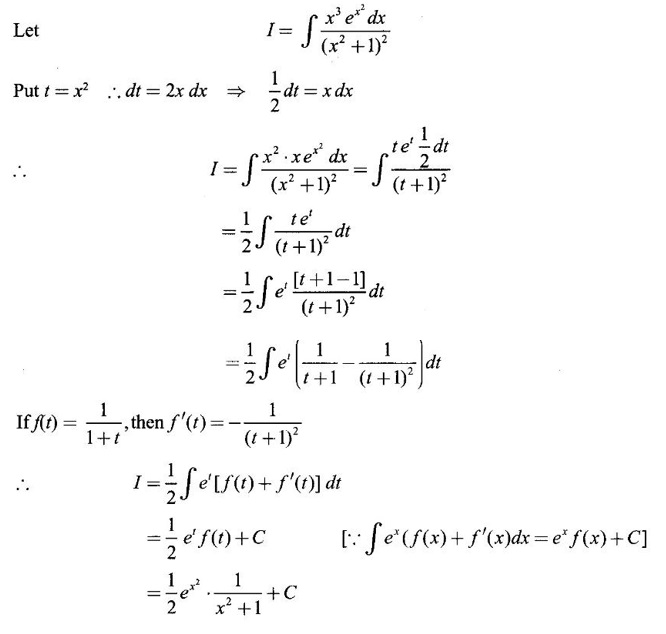

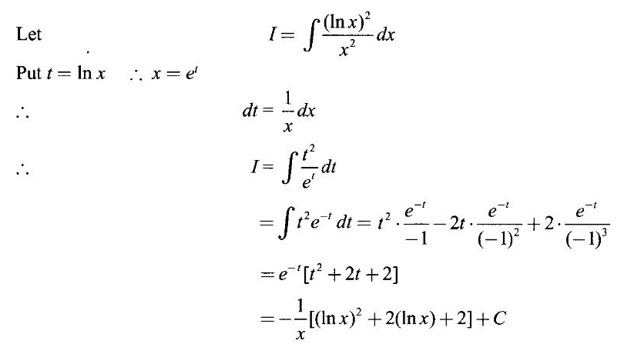
1. Bernoulli's Formula
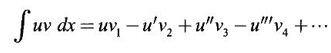


2. Special Integrals
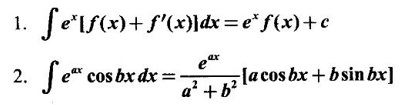




WORKED EXAMPLES





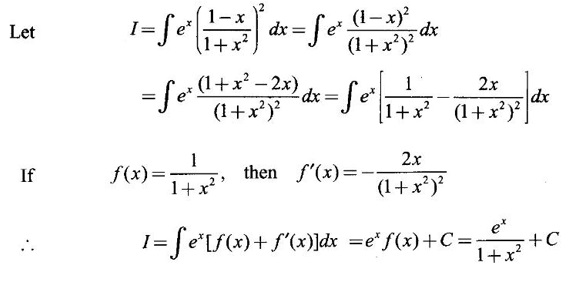
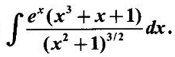

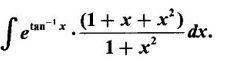


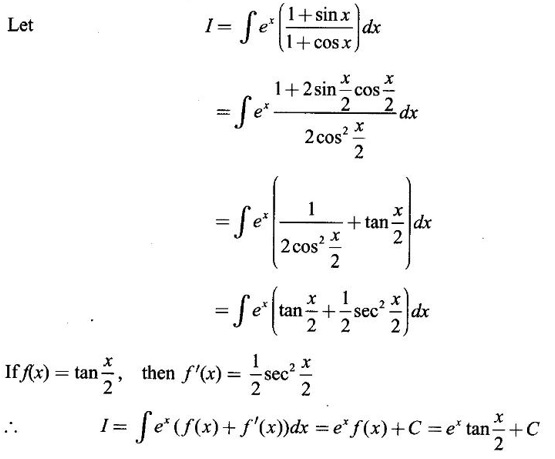


3. Reduction Formula
 cannot be evaluated directively. Applying integration by parts, we can reduce an integral with index n > 0, called the order of the integral, to an integral of the reduced order with a smaller index. The relation between the given integral and the reduced integral of lower order is called the reduction formula.
cannot be evaluated directively. Applying integration by parts, we can reduce an integral with index n > 0, called the order of the integral, to an integral of the reduced order with a smaller index. The relation between the given integral and the reduced integral of lower order is called the reduction formula.WORKED EXAMPLES


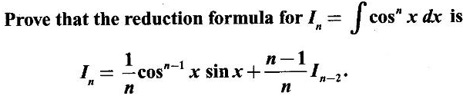

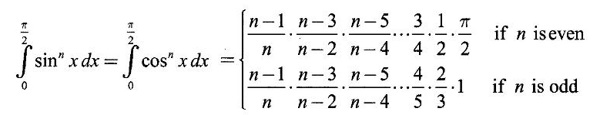

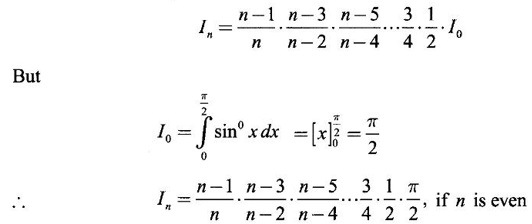









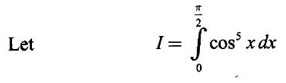


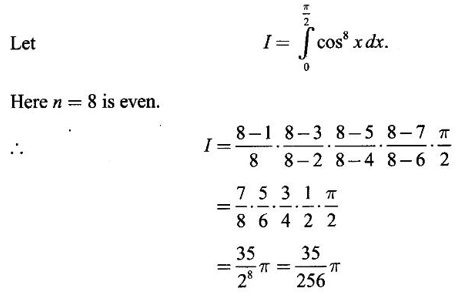
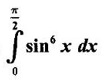
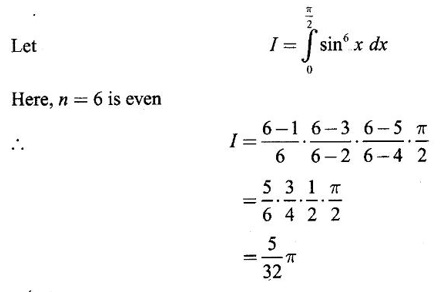
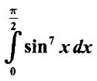

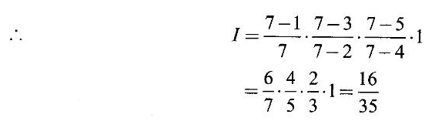
EXERCISE

ANSWERS TO EXERCISE

4. Properties of Definite Integrals

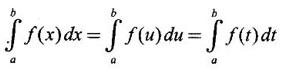


WORKED EXAMPLES
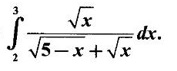
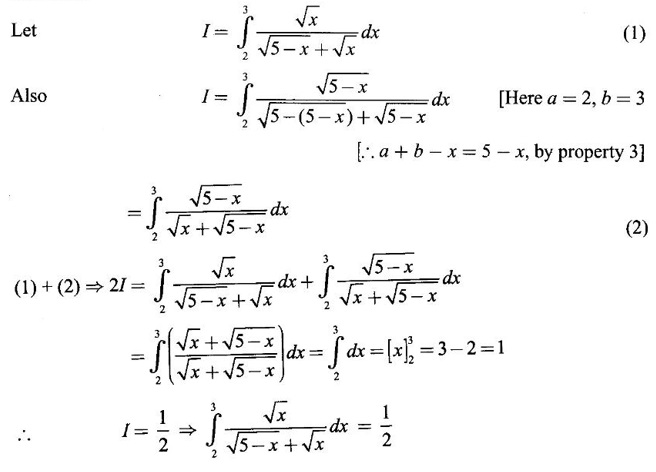



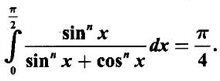




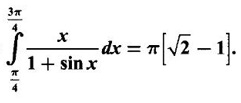

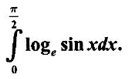






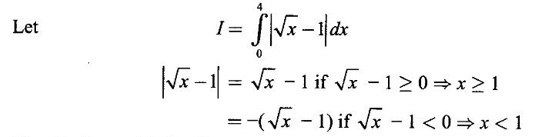
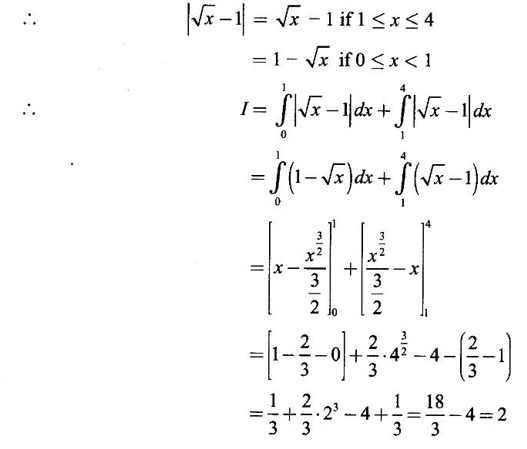
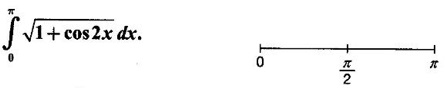


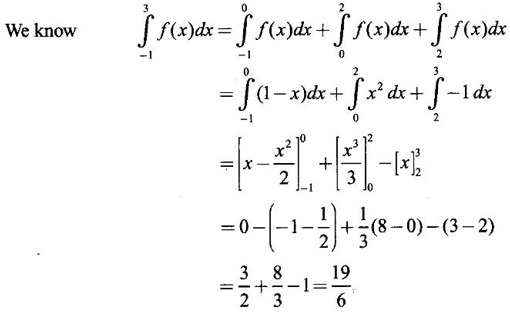



5. Leibnitz Rule for Derivative of Integral
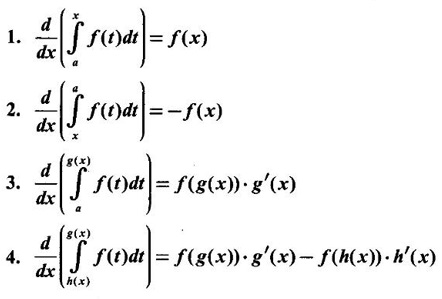
WORKED EXAMPLES



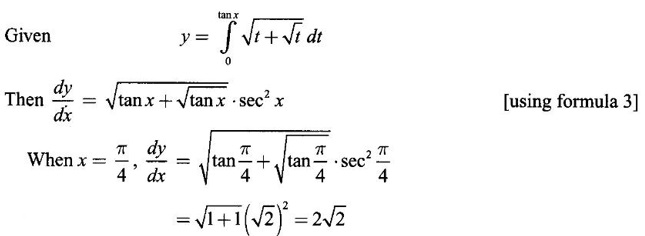

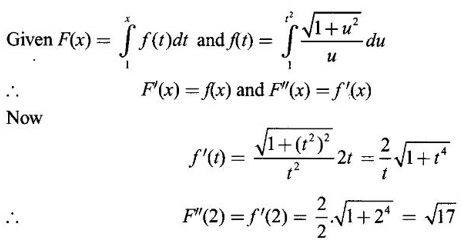
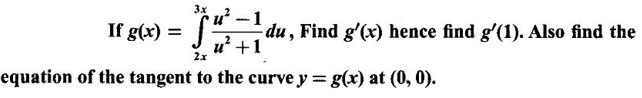

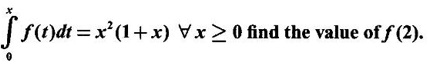
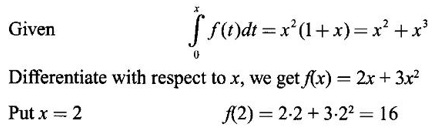

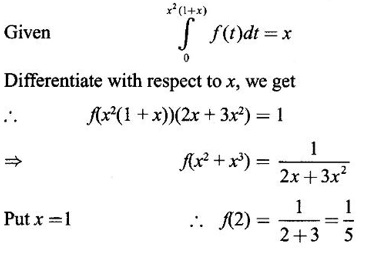

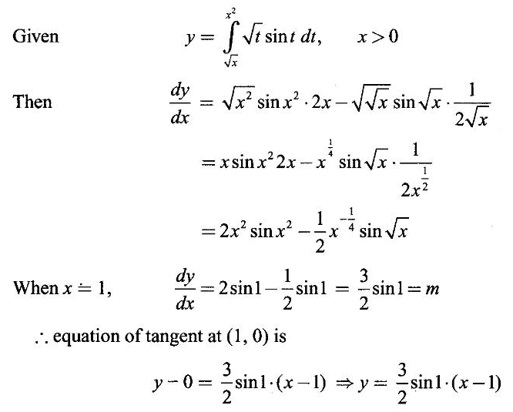

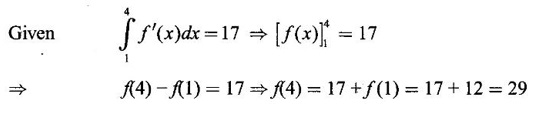

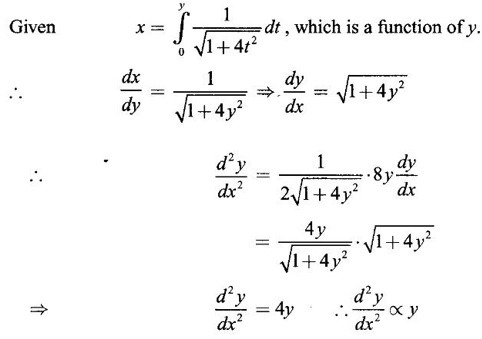
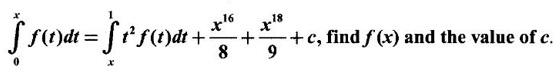

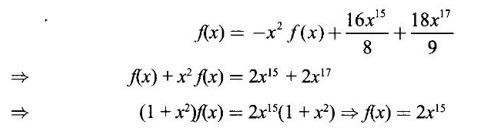

EXERCISE

ANSWERS TO EXERCISE

 as a limit of a sum
as a limit of a sum
WORKED EXAMPLES








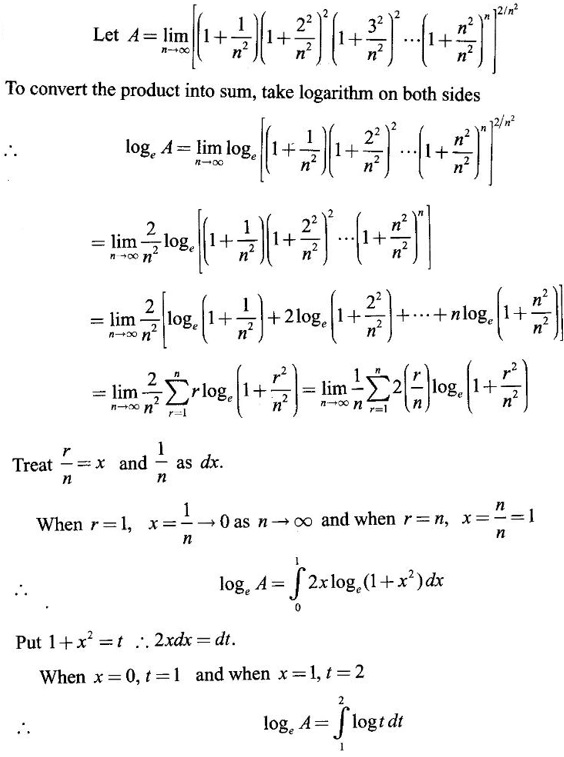
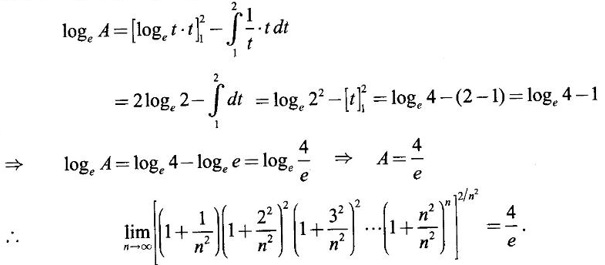
EXERCISE

ANSWERS TO EXERCISE
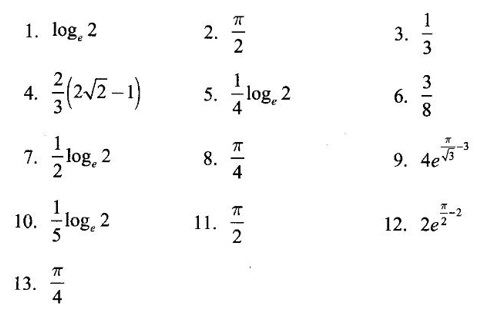
Matrices and Calculus: Unit IV: Integral Calculus : Tag: : Worked Examples, Exercise with Answers | Integral Calculus - Integration by Parts
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
