Matrices and Calculus: Unit IV: Integral Calculus
Indefinite Integral
Worked Examples, Exercise with Answers | Integral Calculus
Further we have the following list of integrals of standard functions from the derivatives of these functions. This list is important for integration.
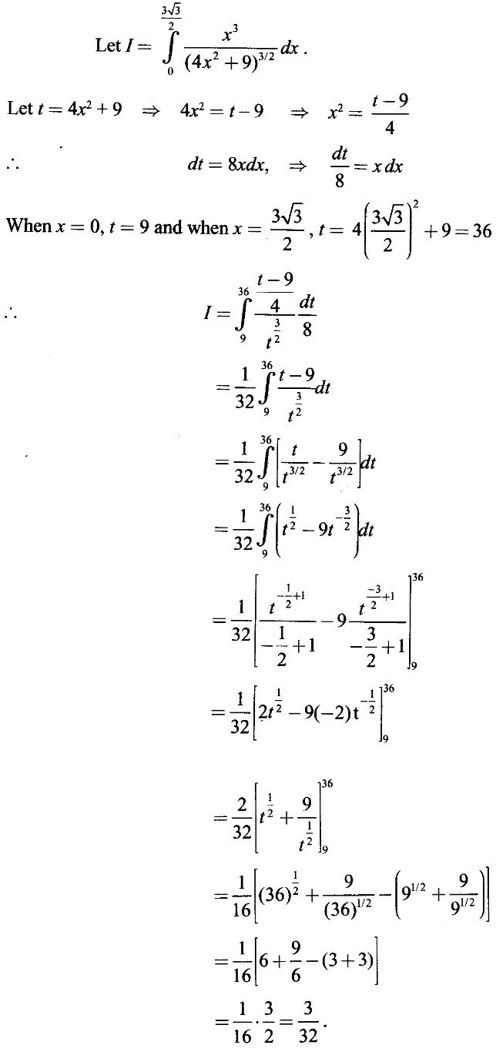
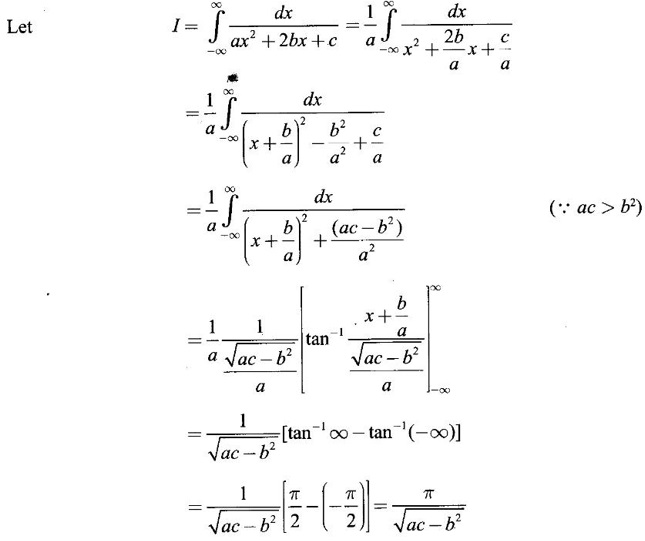
INDEFINITE INTEGRAL If F'(x) = f(x) in an open interval I, then F is called an anti derivative or primitive of f on I. If F(x) is an anti derivative of f(x), then F(x) + C, where C is a arbitrary constant, is an anti derivative, called the general anti derivative. Libnitz used the special symbol ∫ f(x)dx to denote the general anti derivative or general primitive of ƒ and it is called the indefinite integral of f. f(x) is called the integrand and C is constant of integration. dx indicates variable of integration is x. Note: 1. The equation ∫ f(x)dx = F(x) + C is to be considered mearly an alternative way of writing F'(x) = f(x). 2. ∫ f(x)dx represents a family of functions F(x) + C and They have similar notations because the first one is useful in computing the second one. 3. But for the appearance, the symbols ∫ f(x)dx and From the definition of indefinite integral we have the following results, Further we have the following list of integrals of standard functions from the derivatives of these functions. This list is important for integration. There are three main techniques which are used in evaluating integrals. 1. Integration by substitutions 2. Integration by partial fractions 3. Integration by parts Example1 Evaluate ∫ (4x3 − 2x + 3) dx Solution Let Example 2 Evaluate ∫(x + 3)(x − 2)dx Solution Example 3 Evaluate Solution Example 4 Evaluate Solution Example 5 Evaluate Solution Example 6 Evaluate Solution Example 7 Evaluate Solution Example 8 Evaluate Solution Example 9 Evaluate Solution Example 10 Evaluate Solution = tan x - cot x + C Example 11 Evaluate ∫(tan x − 2cot x)2dx. Solution = tan x + 4 (-cot x) - 9x + C = tan x - 4 cot x - 9x + C Certain integrals can be reduced to one of the standard forms in the list of integrals by a suitable substitution or transformation of variable. The form of the integrated often suggests the substitutions. If t = g(x) then dt = g'(x) dx. Then ∫f(x)dx will reduce to standard form ∫F(t)dt = G(t) + C . Then rewrite in terms of x. Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Evaluate Solution Example 4 Evaluate Solution Example 5 Evaluate Solution Example 6 Evaluate Solution Example 7 Evaluate Solution Note: It can also be worked out by putting t = x + 5. Do it yourself: Example 8 Evaluate Solution Example 9 Evaluate Solution Example 10 Evaluate Solution Example 11 Evaluate Solution Example 12 Solution You can do this problem by putting t = sin2x. Do it yourself! Example 13 Evaluate Solution Example 14 Evaluate Solution It can also be worked out by putting t = 1 + x2. Do it yourself! Example 15 Find Solution Example 16 Find Solution Example 17 Find ∫ sint(sec2 (cost)dt. Solution Let I = ∫ sint(sec2 (cost)dt Put y = cos t ⸫ dy = -sin t dt ⇒ -dy = sin t dt = - tan y + C = - tan (cos t) + C Example 18 Evaluate Solution Example 19 Evaluate Solution Example 20 Evaluate Solution Example 21 Evaluate Solution Example 22 Find Solution Example 23 Evaluate Solution Example 24 Evaluate Solution Example 25 Find ∫cos x°dx. Solution Example 26 Find Solution Example 27 Evaluate Solution Evaluate the following indefinite integrals 2. Special Type: Reciprocal Form Certain integrals ∫ƒ(x)dx can be evaluated by rewriting in terms of 1/x. Observe the next few examples WORKED EXAMPLES Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Evaluate Solution Example 4 Find Solution Example 5 Evaluate Solution 3. Integration of Trigonometric Functions of Products and Powers Example 1 Evaluate ∫sin 3x⸱sin bx dx. Solution I = ∫sin 3x⸱sin bx dx We convert into a sum or difference. We know cos (A + B) - cos(A + B) = -2 sinA ⸱ sinB Example 2 Evaluate Solution Example 3 Find Solution We know that Example 4 Find ∫ cos2 x · sin3 x dx. Solution Let Example 5 Find Solution Let I = ∫ sin3 x ⋅ cos2x dx [power of sine is odd] Put t = cos x. ⸫ dt = -sin x dx ⇒ - dt = sin x dx Example 6 Find Solution Example 7 Solution Example 8 Evaluate Solution Example 9 Solution Example 10 Evaluate Solution Example 11 Find Solution Let Example 12 Evaluate Solution Example 13 Find Solution Example 14 Find Solution Type 1: The Integrals of the Form where numerator and denominator are functions of the first degree in sinx or cosx or both. To evaluate it, put l sin x + m cos x = A d/dx (a sin x + b cos x) + B(a sin x + b cos x) Example 1 Evaluate Solution Equating coefficients of sin x on both sides, we get -4A + 5B = 3 (1) Equating coefficients of cos x on both sides, we get 5A + 5B = 2 (2) Solve (1) and (2) to find A, B Substituting in (1), we get Example 2 Evaluate Solution Type 2 In the following problems we choose the substitution t in terms of sin x and cos x, so that dt is the numerator. Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Evaluate Solution Type 3 Example 1 Solution Example 2 Solution Example 3 Find Solution Example 4 Find Solution 3. Integration of Irrational Functions by Trigonometric Substitutions When the integrand contains expressions of the form Example 1 Evaluate Solution Example 2 Solution Example 3 Evaluate Solution Example 4 Evaluate Solution Example 5 Evaluate Solution Evaluate the following integrals 4. Integration of Rational Algebraic Functions If the degree of the numerator is greater than or equal to the degree of the denominator, We divide till the remainder degree is less than the degree of denominator. Example 1 Find Solution Example 2 Find Solution Example 3 Show that Solution Being rational function divide the Numerator by the Denominator Example 4 Find Solution 5. Integration by Partial Fractions If the integrand is a proper rational function and the denominator is factorisable into rational factors of first degree or second degree, then the integrand can be expressed into partial fractions. Then we integrate. Example 1 Evaluate Solution Since degree of numerator is less then the degree of denominator i.e., the integrand is a proper fraction, we use partial fraction method. Example 2 Evaluate Solution Since the degree of numerator is less than the degree of denominator, it is a proper fraction. We use partial function method. Multiplying both sides by x(2x − 1)(x + 2), we get Example 3 Evaluate Solution Since degree of numerator is less than the degree of denominator. We use partial fraction method. Here the denominator contains repeated factor (x − 1)2 Note: For repeated factor (x − 1)2 there will be 2 terms as written in the Example 3. For a second degree factor assume numerator as first degree ax + b. Example 4 Evaluate Solution Example 5 Solution Example 6 Evaluate Solution The numerator degree is less than the denominator degree. So, it is a proper fraction with denominator containing repeated factor and second degree factor. Equating co efficient of x, we get Equating coefficients of x, we get Example 7 Evaluate Solution Multiplying by (x - 1) (x - 2), we get 7x – 6 = A(x - 2) + B(x - 1) Put x = 1, then 7 - 6 = A(1−2) ⇒ -A = 1 ⇒ A = -1 Put x = 2, then 14 - 6 = B(2 − 1) ⇒ B = 8 Evaluate the following integrals: Special Cases Example 1 Evaluate Solution Put t = 0, then I = A Example 2 Evaluate Solution Let Put x + 1 = tan θ ⸫ dx = sec2 θ dθ Example 3 Evaluate Solution Since there is no odd powers of x and the denominator factors are of the form x2 ± a2, the partial fraction can be written treating x2 as variable y. Example 4 Evaluate Solution Example 5 Evaluate Solution Example 6 Evaluate Solution Type 1: Integrals of the Form where ax2 + bx + c cannot be factorized into real factors. In the first integral, take out a and completing squares it will reduce to one of the forms Equating the coefficients find A and B. Then integrate w. r. to x. One integral will be of type (1) and the other is of the form Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Prove that Solution Example 4 Solution Equating constant terms, we get Example 5 Evaluate Solution Equating constants terms, Example 6 Evaluate Solution Type 2: Integrals of the form (1) (1) is evaluated by completion of squares method and using the formulae (2) is evaluated by putting Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Evaluate Solution Example 4 Evaluate Solution Example 5 Evaluate Solution Example 6 Evaluate Solution Type 3 by taking out A and completing squares. To evaluate it, we use any one of the formulae given below. Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Evaluate Solution Type 4: Integrals of the form In (i) take out a and complete the squares and it will reduce to the form To evaluate it, we use any one of the formulae given below. Example 1 Evaluate Solution Example 2 Evaluate Solution Example 3 Evaluate Solution Example 4 Solution Example 5 Evaluate Solution Evaluate the following integrals
 represents a number.
represents a number.![]() f(x)dx originate from two different processes differentiation and integration.
f(x)dx originate from two different processes differentiation and integration.

WORKED EXAMPLS
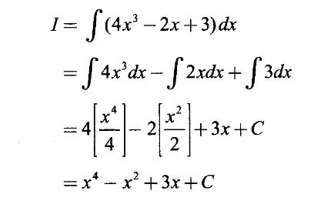
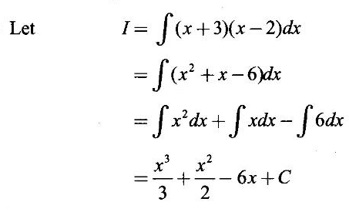



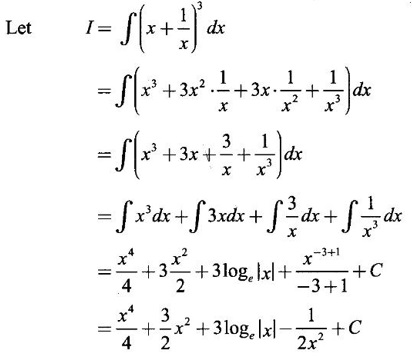
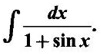

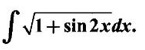





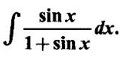




1. Integration by Substitution
WORKED EXAMPLES
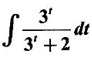
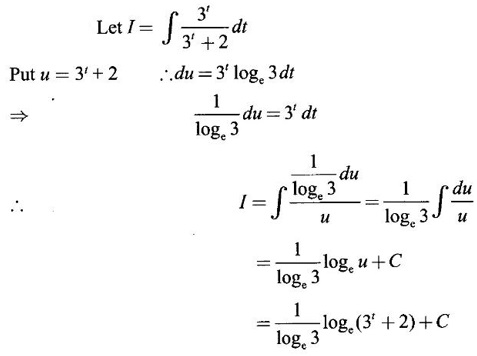



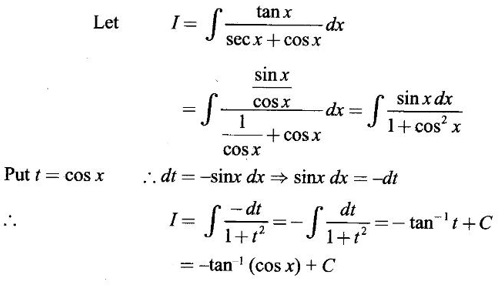



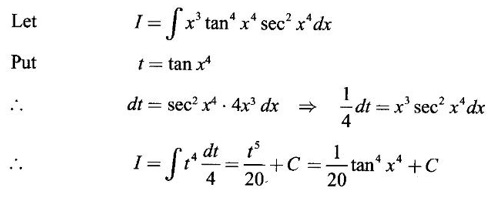

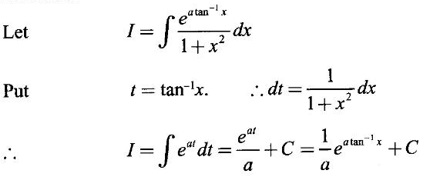

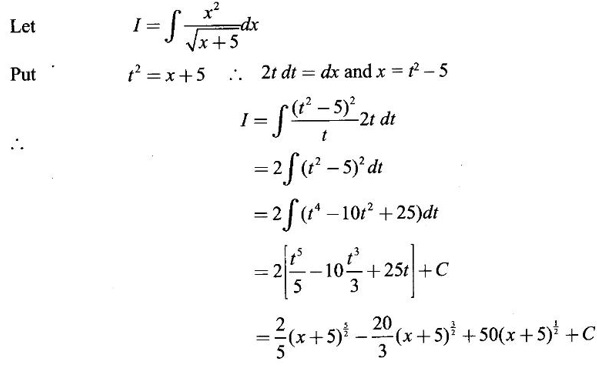
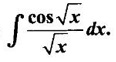
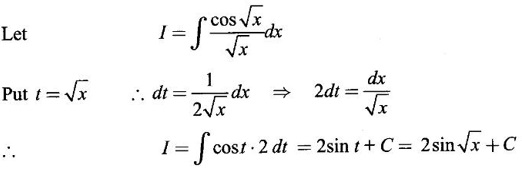

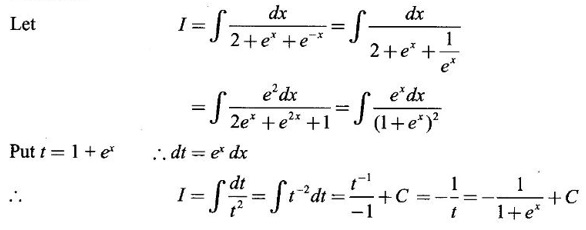
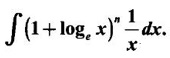



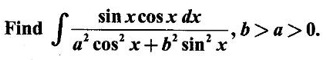
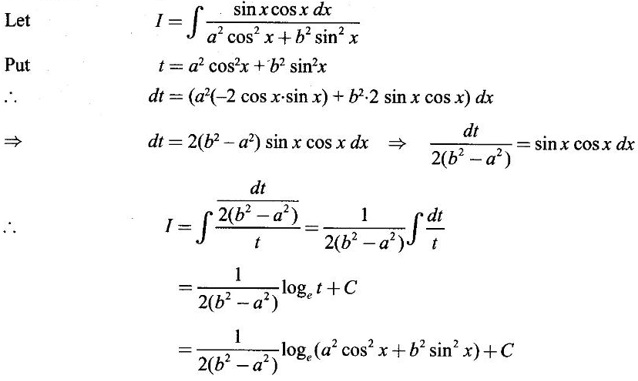

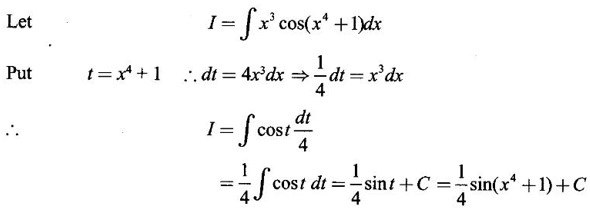
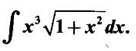
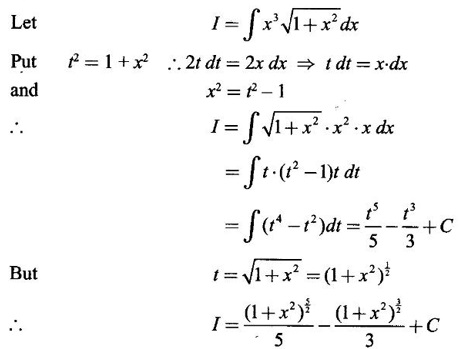




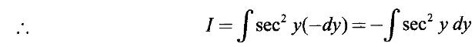

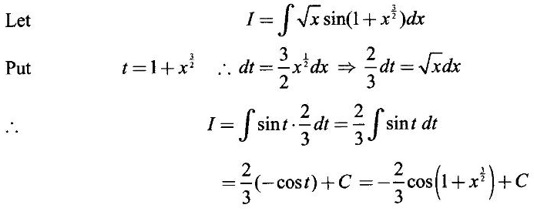
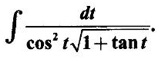
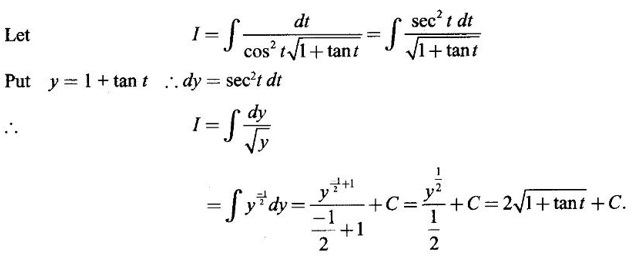

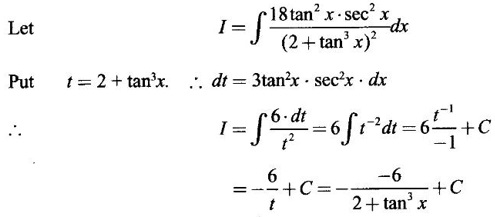


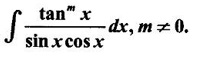

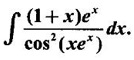



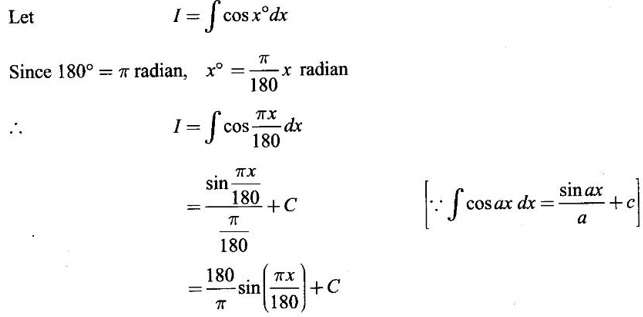

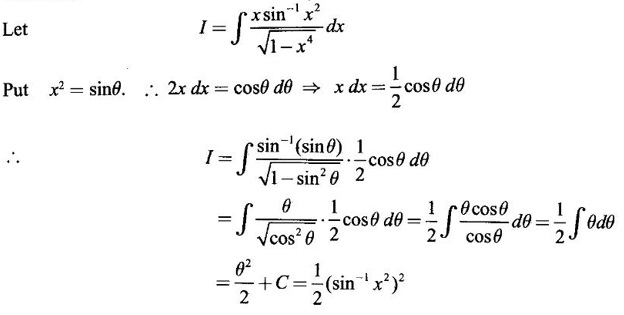
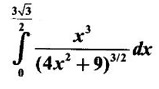
EXERCISE

ANSWERS TO EXERCISE
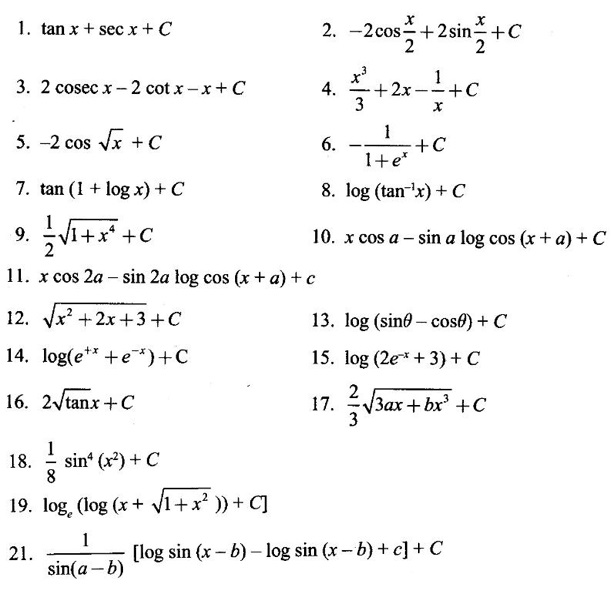
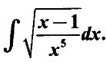

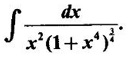



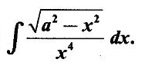


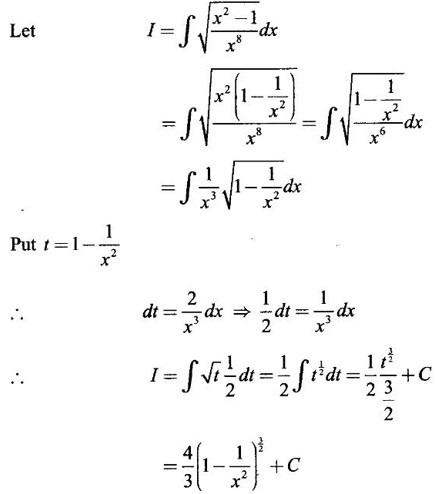
WORKED EXAMPLES



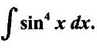










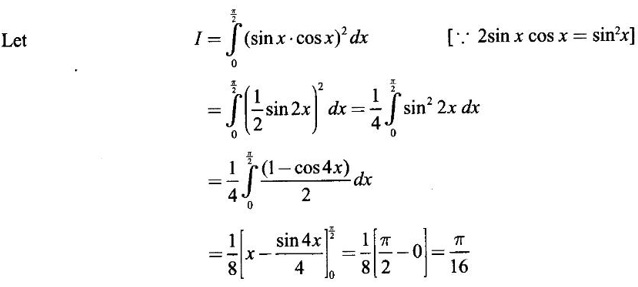
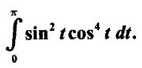
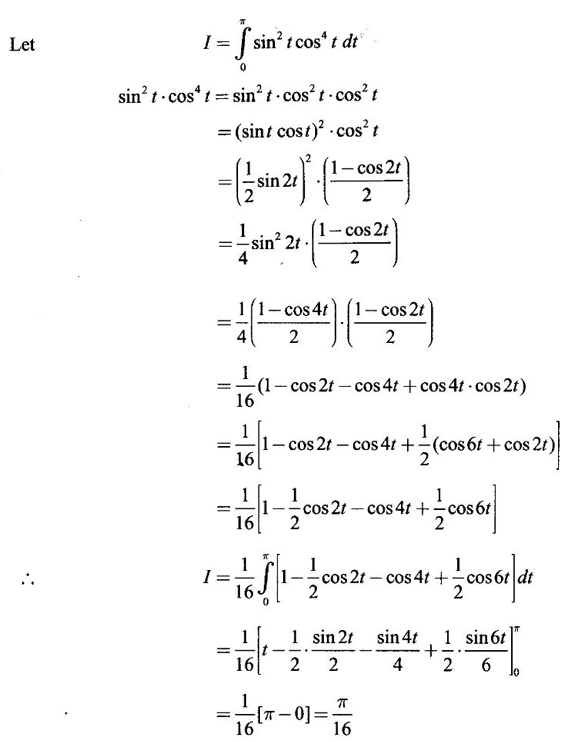

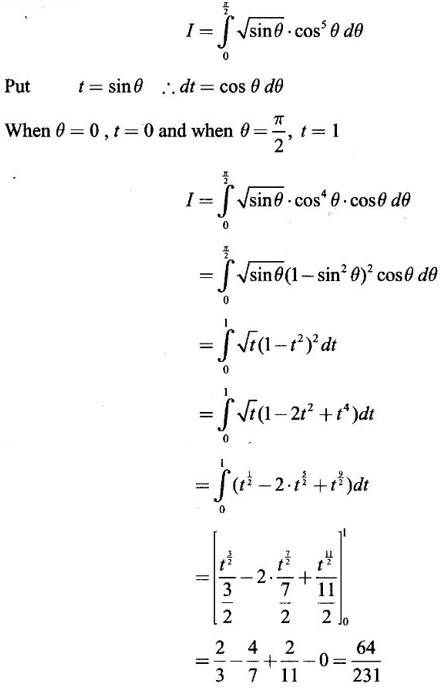
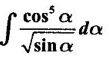


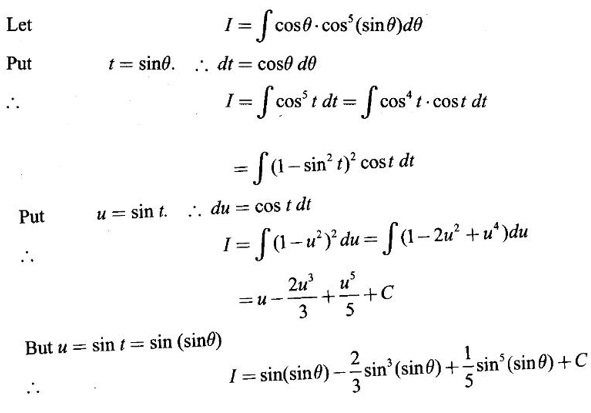
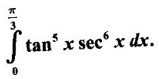
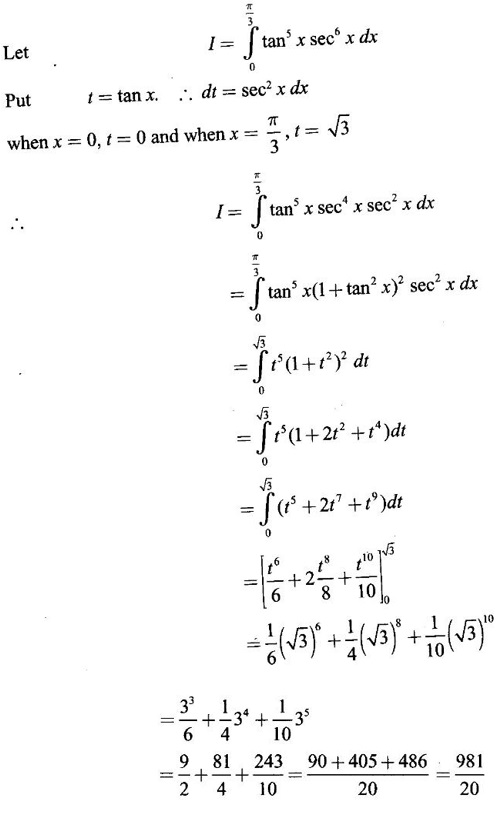


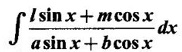
WORKED EXAMPLES






WORKED EXAMPLES







WORKED EXAMPLES


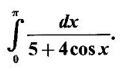

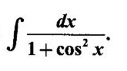
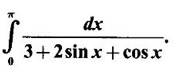
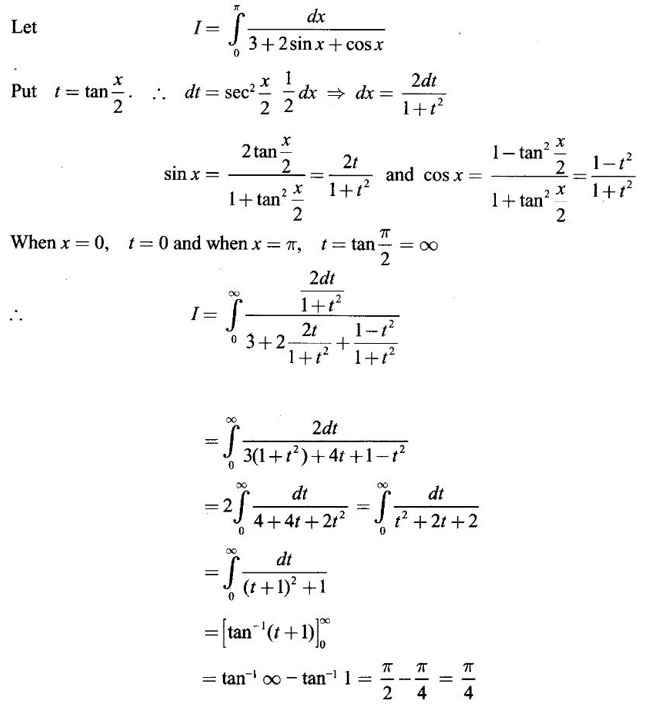
EXERCISE

ANSWERS TO EXERCISE
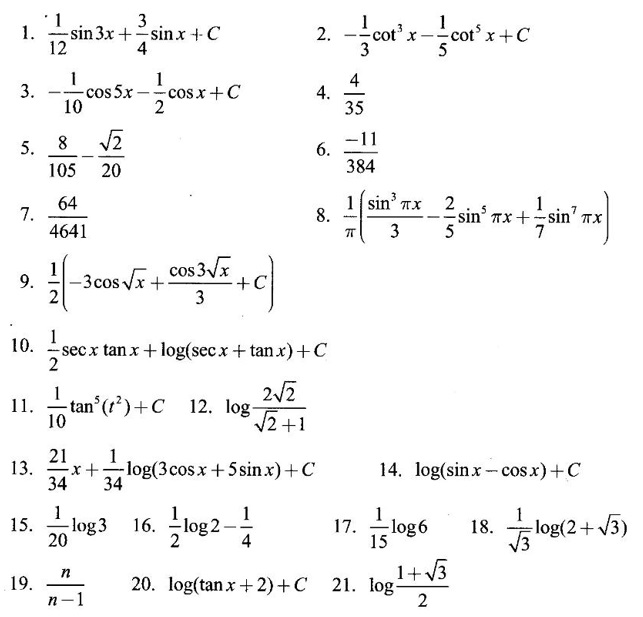

WORKED EXAMPLES


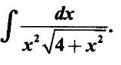



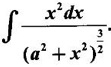

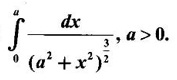

EXERCISE

ANSWERS TO EXERCISE
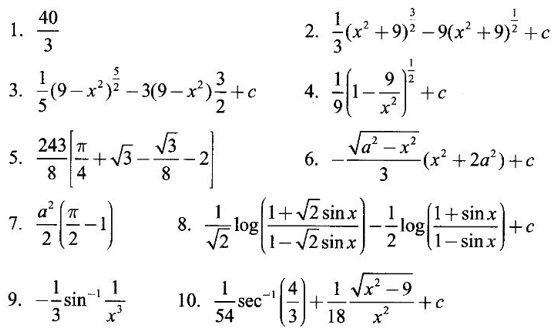
WORKED EXAMPLES
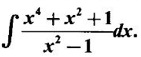




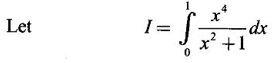


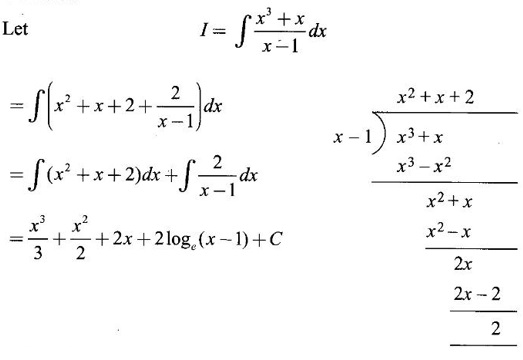
WORKED EXAMPLES










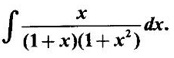
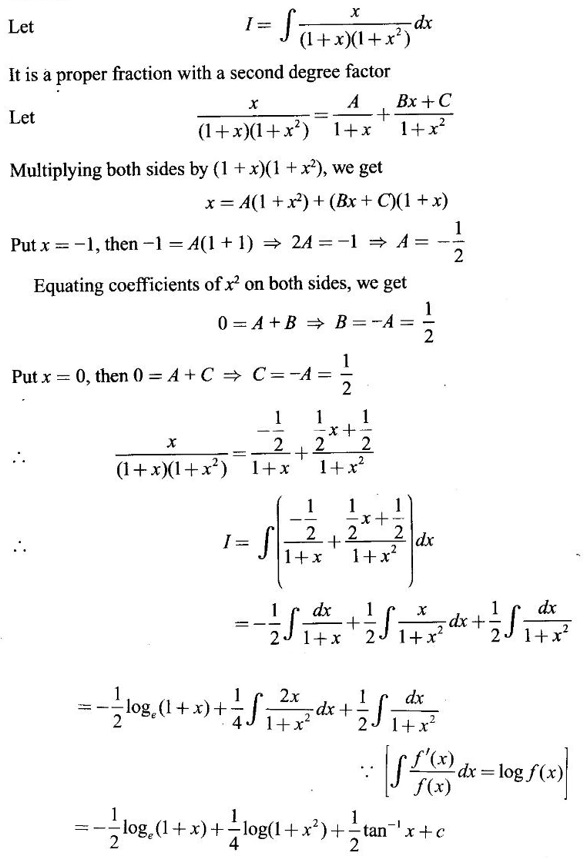



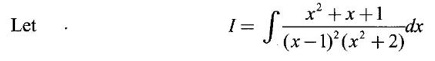
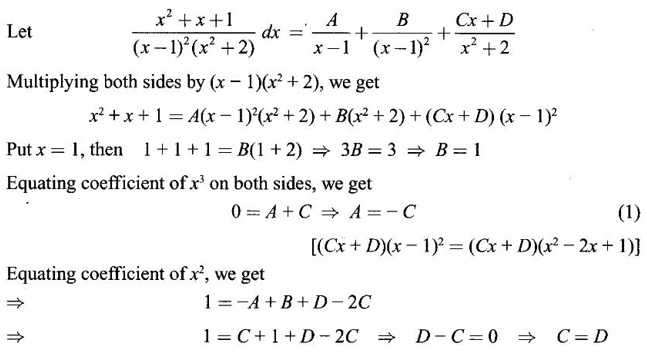

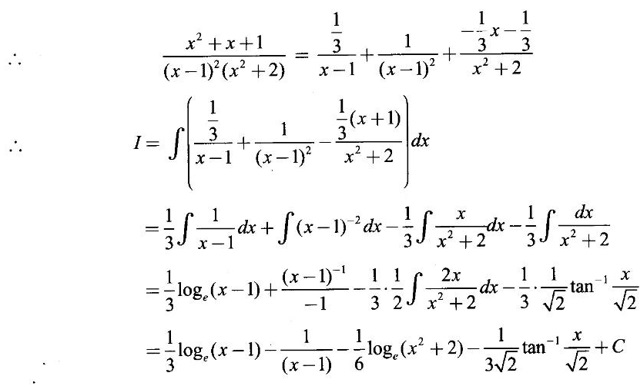

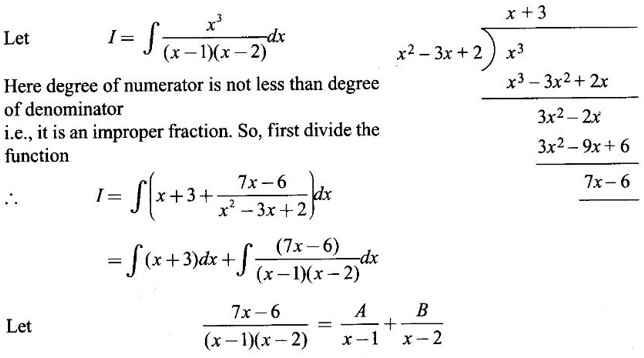
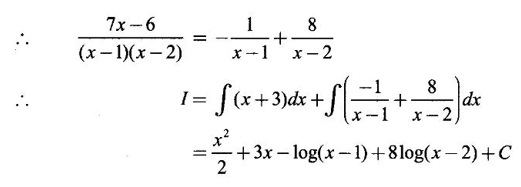
EXERCISE

ANSWERS TO EXERCISE

WORKED EXAMPLES
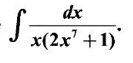

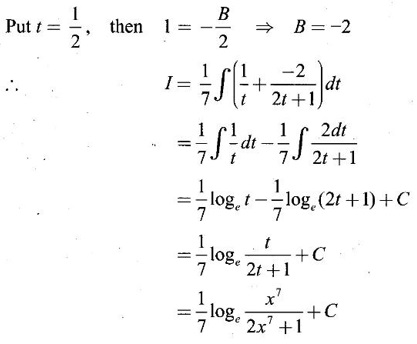




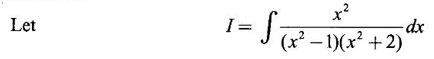







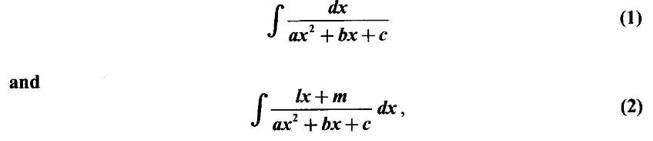



WORKED EXAMPLES



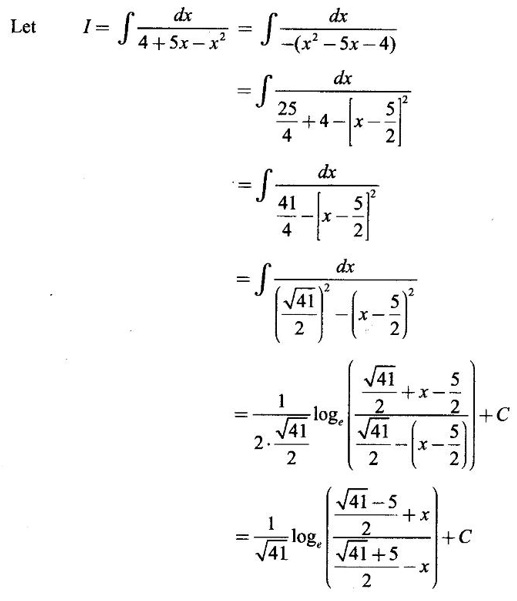







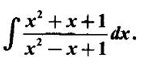

 and (2)
and (2) 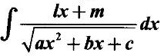
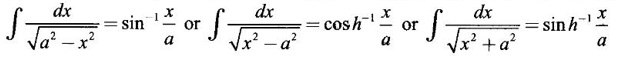
 and proceeding as above.
and proceeding as above.WORKED EXAMPLES



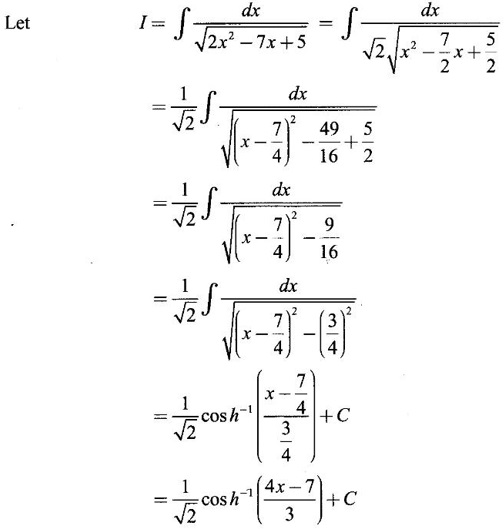


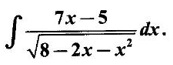





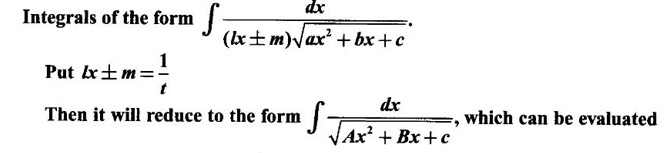
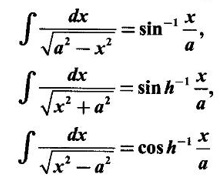
WORKED EXAMPLES
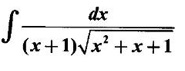
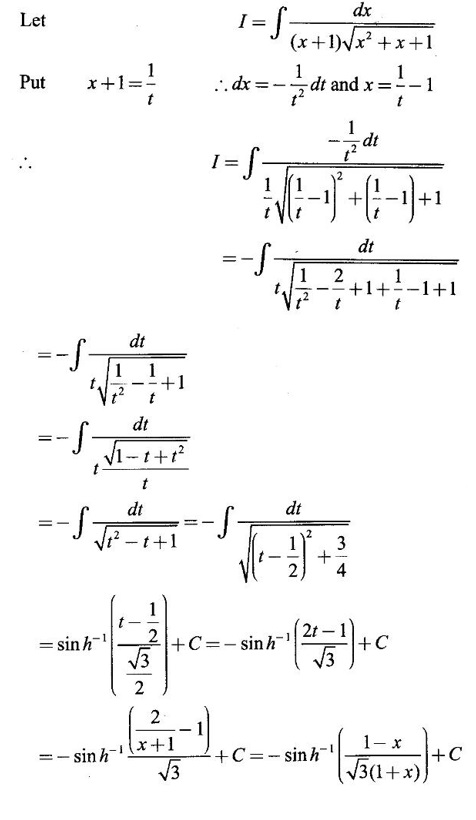
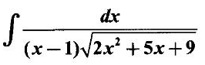
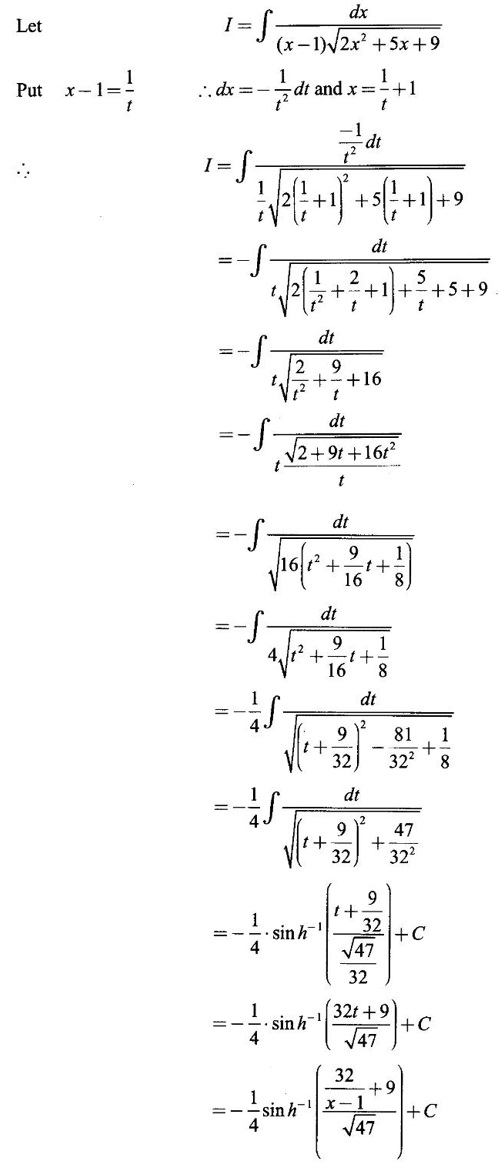
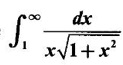




WORKED EXAMPLE


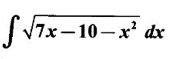







EXERCISE

ANSWERS TO EXERCISE

Matrices and Calculus: Unit IV: Integral Calculus : Tag: : Worked Examples, Exercise with Answers | Integral Calculus - Indefinite Integral
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
