Matrices and Calculus: Unit IV: Integral Calculus
Improper Integrals
Theorem, Worked Examples, Exercise with Answers | Integral Calculus
there are many practical problems where ƒ is unbounded on [a, b] or the interval is not finite. Such integrals are known as improper integrals.
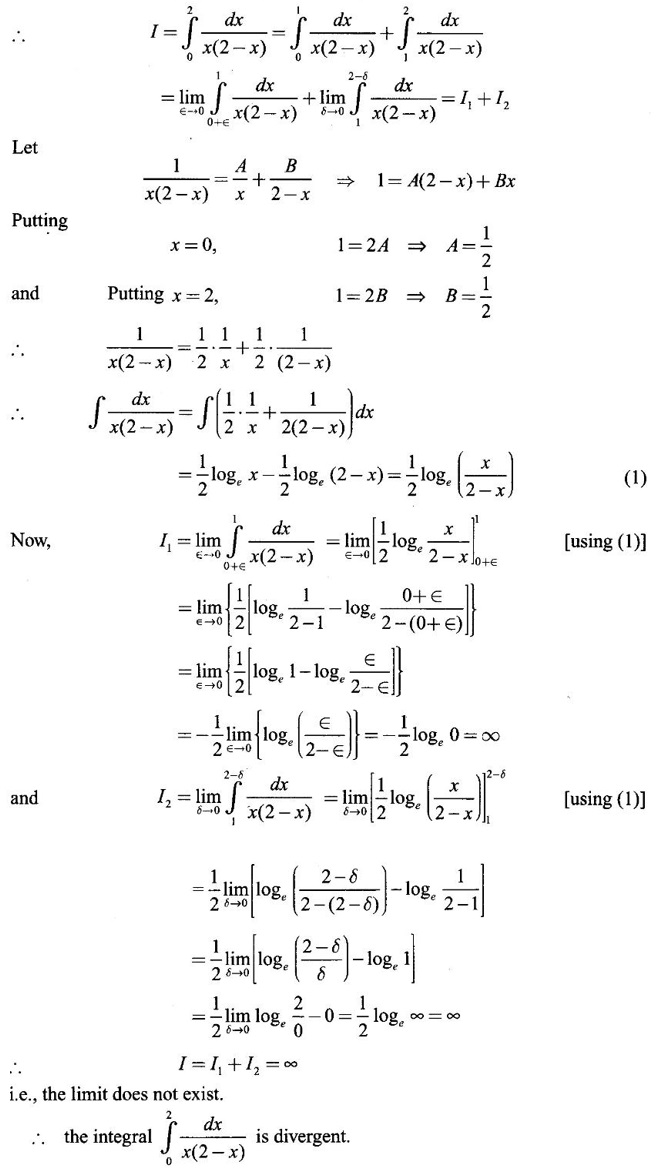
IMPROPER INTEGRALS The definite integral Then But there are many practical problems where ƒ is unbounded on [a, b] or the interval is not finite. Such integrals are known as improper integrals. For example: (a) Improper integrals of the first kind Note The integral (b) Improper integrals of the second kind If the interval [a, b] is finite and f is unbounded at one or more points on [a, b], then 1. If f is unbounded at a only (i.e., ƒ has an infinite discontinuity at a), then we define (ii) the limit exists and is equal to A. Remark: Cauchy's Principal Value Problems based on improper integral of the first kind Example 1 Evaluate the improper integral Solution Example 2 Evaluated Solution Example 3 Evaluate Solution When x = a, t = a2 and when x = 0, t = 0 Example 4 Evaluate Solution Example 5 Evaluate Solution But sin a and cos a oscillate finitely between -1 and +1. Since a cos a → as a → ∞, limit is ∞ Example 6 Evaluate Solution Example 7 Evaluate Solution Example 8 Solution Example 9 Evaluate Solution Put x = 0, then 3 = A – C ⇒ C = A - 3 = 2 − 3 = −1 Equating coefficients of x2, 0 = A + B ⇒ B = -A = -2 Example 10 Evaluate the improper integral Solution When v = 0, Problems based on improper integral of the second kind Example 11 Evaluate the improper integral Solution Let Example 12 Evaluate the improper integral Solution Let ⸫ f(x) is unbounded at x = 1. ⸫ the integrand is unbounded when x = 1 and the interval [0, 2] is finite. Hence, it is an improper integral of the second kind. Example 13 Evaluate the improper integral Solution ⸫ f(x) is unbounded at x = 0 and x = 2 ⸫ the integrand is unbounded and the interval [0, 2] is finite. Hence, it is an improper integral of the second kind. Example 14 Evaluate the improper integral Solution Let As x→0 +, loge x → ∞. So, f(x) is unbounded at x = 0. ⸫ the integrand is unbounded and the interval [-1, 1] is fininte. Hence, it is an improper integral of the second kind. But Now Example 15 Evaluate Solution Let Hence, it is an improper integral of the second kind Here Test the convergence of the following improper integrals using definition. Find the value if convergent. As in the case of series of positive terms, we have tests for convergence of improper integrals with positive integrand. (a) Tests of convergence of improper integrals of the first kind We state the following theorems without proof. Theorem 4.2 Comparison Test Theorem 4.3 Note The above result is equivalently, if Limit form of comparison test That is both the integrals behave alike. Note As in the case of series, here also we consider the following improper integrals for comparison, Absolute Convergence Example 1 Test the convergence of Solution Example 2 Test the convergence of Solution ⸫ by the comparison test, Example 3 Test the convergence of Solution Example 4 Test the convergence of Solution Let ⸫ 0 is not a point of infinite discontinuity. Example 5 Test the convergence of Solution Example 6 Test the convergence of Solution Example 7 Test the convergence of Solution Example 8 Test the convergence of Solution (b) Test of convergence of Improper Integrals of the second kind We state the following theorems without proof. Theorem 4.5 Comparison Test Theorem 4.6 Limit form of comparison test Theorem 4.7 Note Improper integrals for comparison Example 1 Test the convergence of the improper integral Solution Example 2 Test the convergence of the improper integral Solution Example 3 Test the convergence and evaluate the improper integral Solution Example 4 Test the convergence of the improper integral Solution Example 5 Prove that Solution The function is bounded, but the interval is infinite. So, it is improper integral of the first kind. ⸫ 0 is not a discontinuity. Note Similarly, we can prove These two integrals are called Fresnel's integrals. They are useful in explaining the concept of light diffraction. Example 6 Show that Solution Example 7 Solution Let Integrating by parts, Test the convergence of the following improper integrals. 1. convergent 2. divergent 3. convergent 4. divergent 5. convergent 6. convergent 7. convergent 8. divergent 9. convergent 10. convergent 11. convergent 12. convergent 13. convergent 14. convergent 15. divergent 16. divergent 17. convergent if n < 2 18. convergent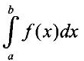 is defined as the limit of a sum under two conditions (i) the interval [a, b] is of finite length and (ii) f is defined and bounded on [a, b].
is defined as the limit of a sum under two conditions (i) the interval [a, b] is of finite length and (ii) f is defined and bounded on [a, b].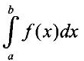 is called a proper integral.
is called a proper integral.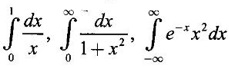 are improper integrals.
are improper integrals.1. Kinds of Improper Integrals and their Convergence

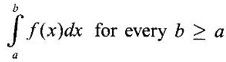 for every b ≥ a is analogus to "partial sum” in infinite series and so it may be considered as "partial integral".
for every b ≥ a is analogus to "partial sum” in infinite series and so it may be considered as "partial integral".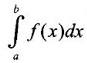 is called an improper integral of the second kind.
is called an improper integral of the second kind.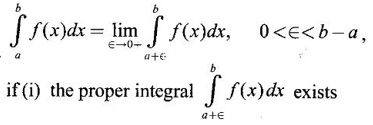


WORKED EXAMPLES
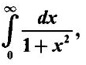 if it exists.
if it exists.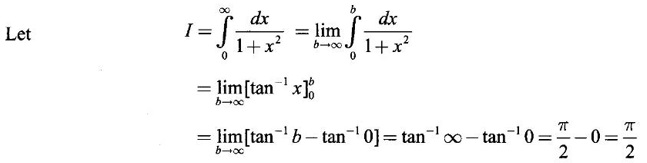
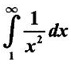 if it exists.
if it exists.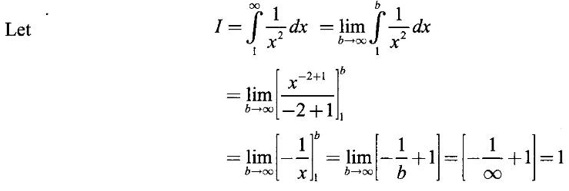
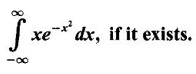
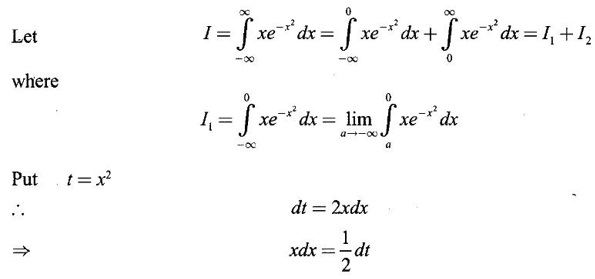
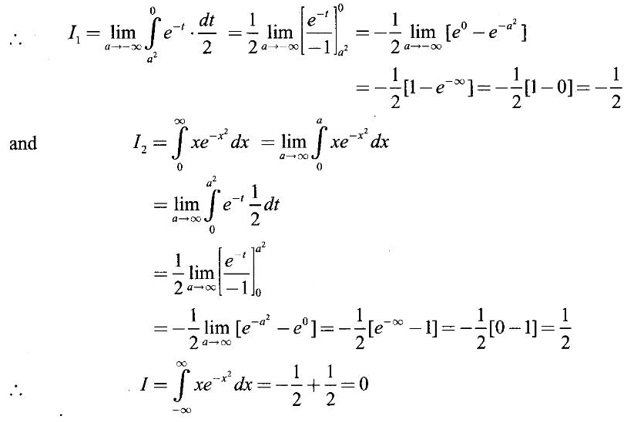
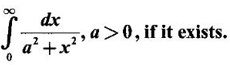
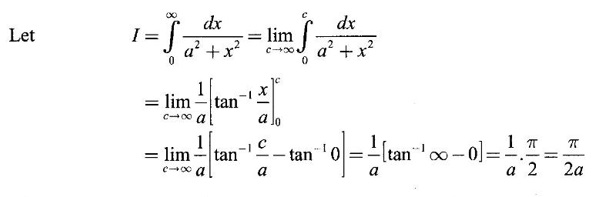
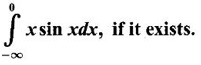
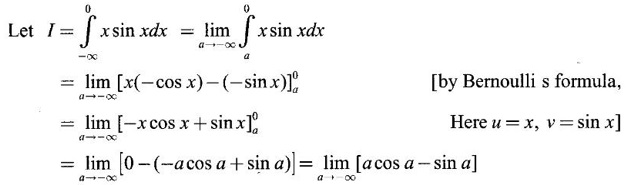
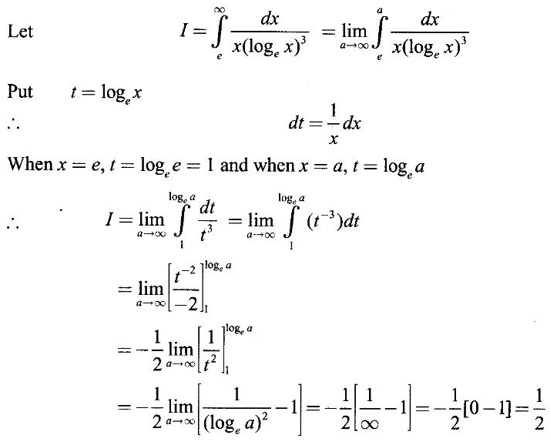
 if it exists.
if it exists.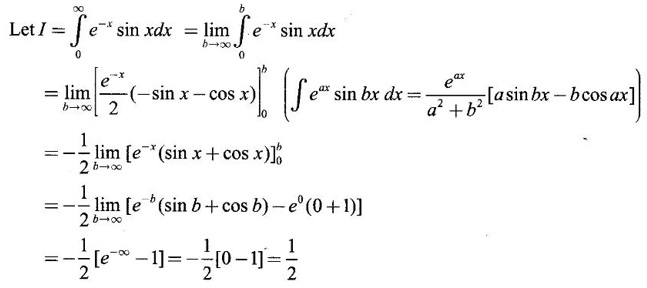
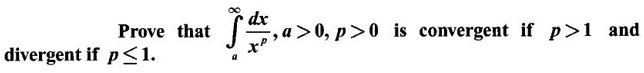
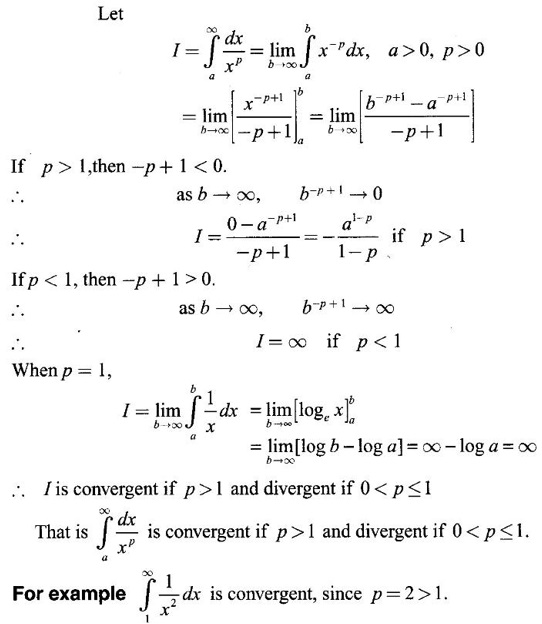
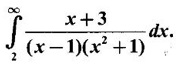
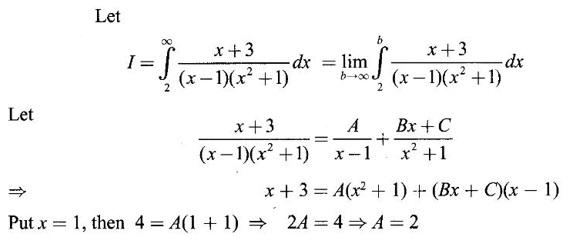

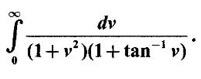
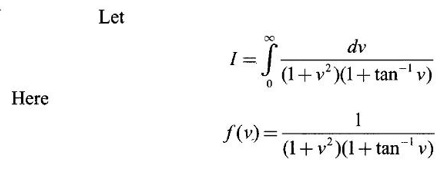

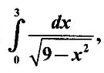 if it exists.
if it exists.
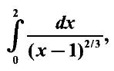 if it exists.
if it exists.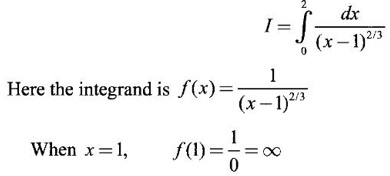

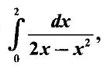 if it exists.
if it exists.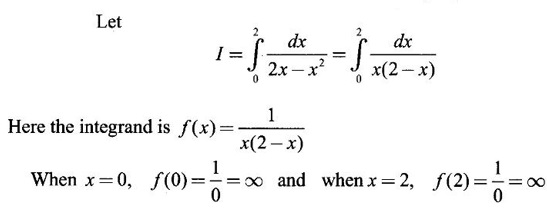
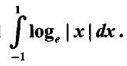
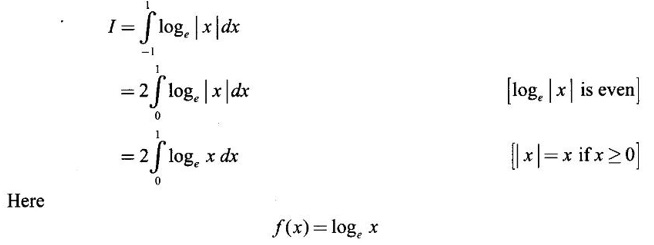
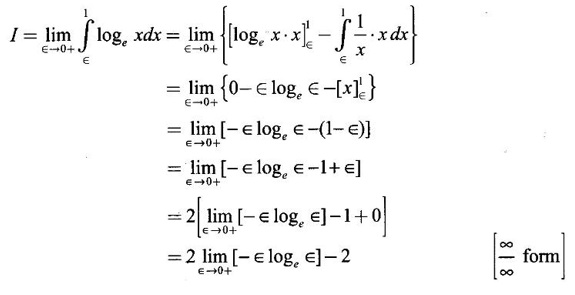

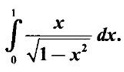
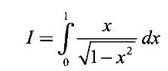

EXERCISE
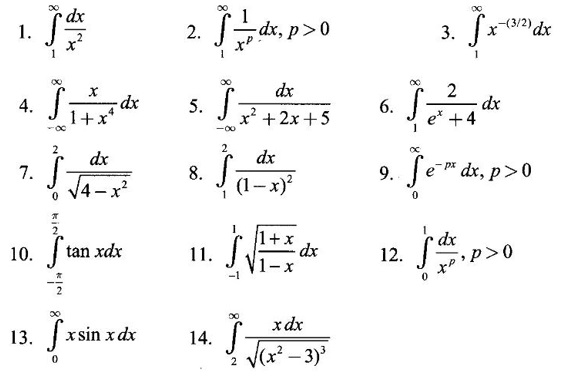
ANSWERS TO EXERCISE

2. Tests of Convergence of Improper Integrals
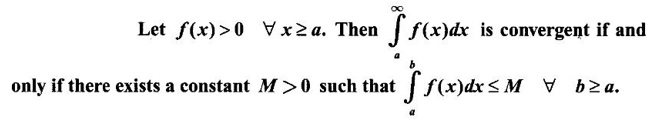
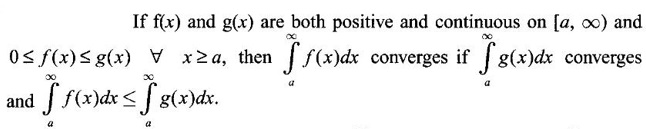
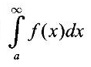 diverges, then
diverges, then 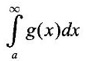 diverges.
diverges.Theorem 4.4
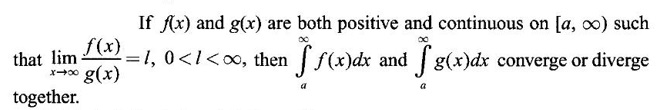
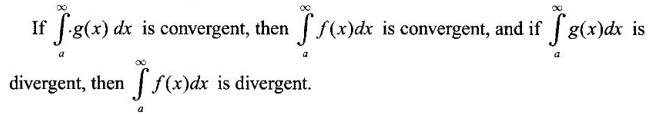
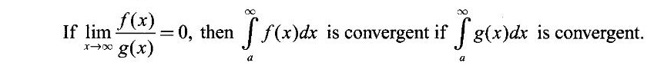

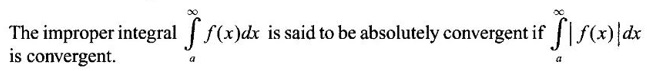
WORKED EXAMPLE:
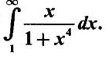

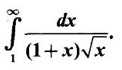
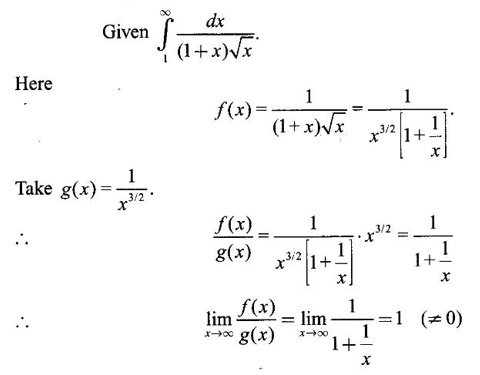
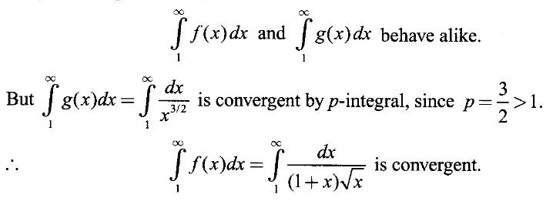
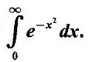

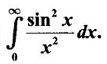
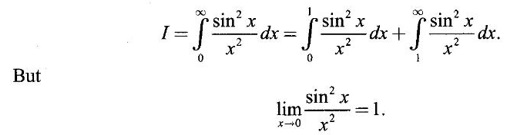

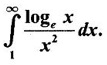

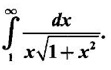

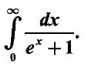

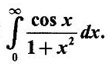

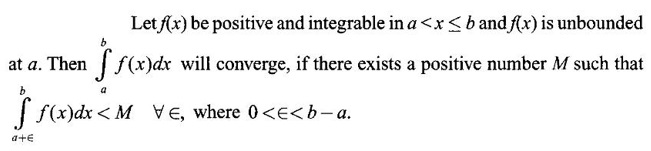
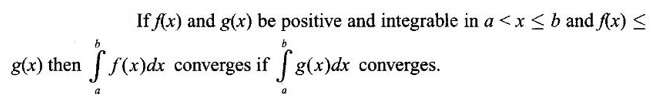
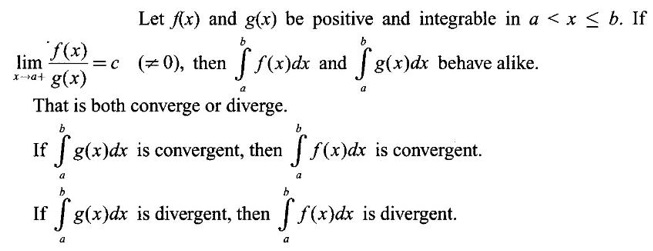
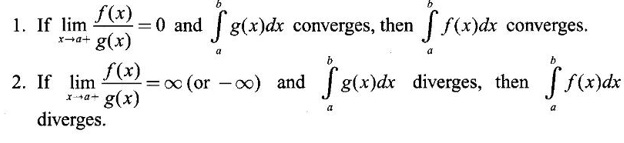
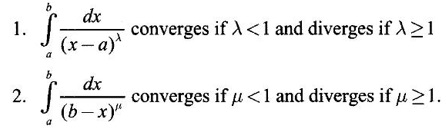
WORKED EXAMPLES
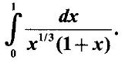

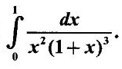
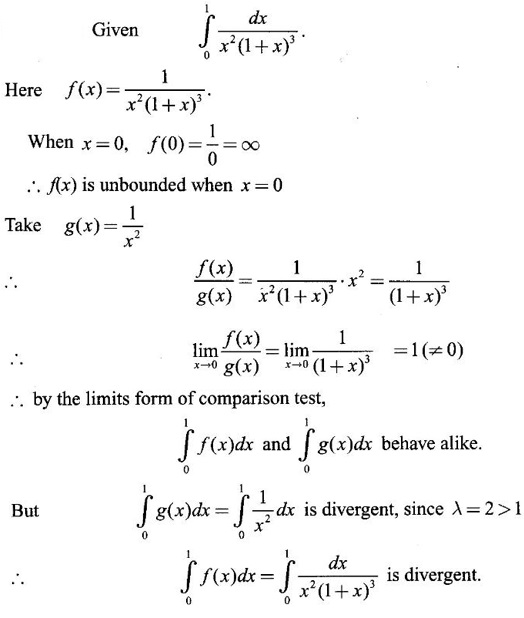
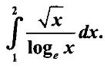

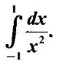

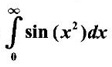 converge.
converge.


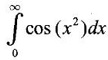 is convergent.
is convergent.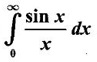 converges.
converges.

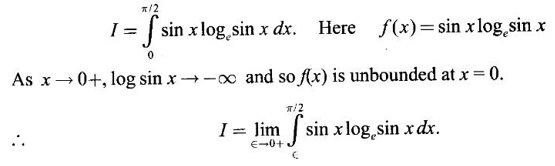

EXERCISE

ANSWERS TO EXERCISE
Matrices and Calculus: Unit IV: Integral Calculus : Tag: : Theorem, Worked Examples, Exercise with Answers | Integral Calculus - Improper Integrals
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
