Matrices and Calculus: Unit II: Differential Calculus
Implicit Differentiation
Worked Examples | Differential Calculus
So far, we have seen differentiation of function given by equations of the form y = f(x), where y is written explicitly in terms of x.
IMPLICIT DIFFERENTIATION So far, we have seen differentiation of function given by equations of the form y = f(x), where y is written explicitly in terms of x. The function is then said to be in explicit form. But in practical situations we come across equations such as x3 + y3 = 3xy, where y cannot be written in terms of x explicitly. Such an equation is in the form of F(x, y) = 0, where y is defined implicitly as a function of x, is said to be in implicit form. To differentiate the functions in implicit form, we treat y as a function of x and differentiate with respect to x. This type of differentiation is known as implicit differentiation. This technique is illustrated in the following examples. Example 1 Solution Given x2 + xy − y2 = 10 (1) It is implicite function. ⸫ differentiating w. r. to x, we get Example 2 Solution Example 3 Find y' and y" if x4 + y4 = 4 Solution Given x4 + y4 = 4 (1) It is implicit function Differentiating (1) w. r. to x, we get Differentiating (2) w. r. to x, we get From (2), we get Substituting in (3), we get Example 4 Solution Given the implicit form x2 - y2 + sin (xy) = 0 Differentiating with respect to x, treating y as a function of x, we get Example 5 Solution Given the implicit form x3 + y3 = 6xy Differentiating with respect to x, treating y as a function of x, we get Dividing by 3, we get Example 6 Solution Given the implicit form sin y = x sin(a + y) Differentiating with respect to y, we get Example 7 If x2 + xy + y = 1, then find the value of ym at the point where x = 1 Solution From (3), we get ⇒ 2 + 1⸱ yn + 2(-2) + 0 + 0 = 0 ⇒ yn – 2 = 0 ⇒ yn = 2 From (4), we get Example 8 Solution Example 9 Solution Example 10 Solution Given the implicit form Differentiating with respect to x, we getWORKED EXAMPLES
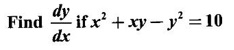
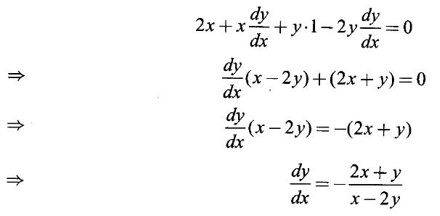
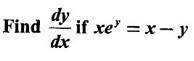
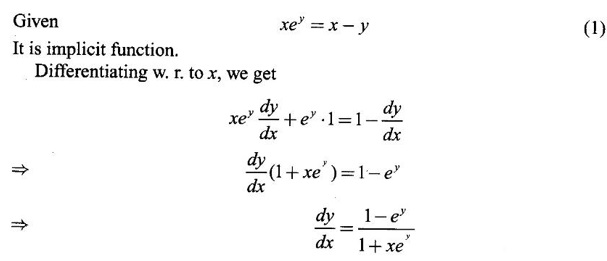
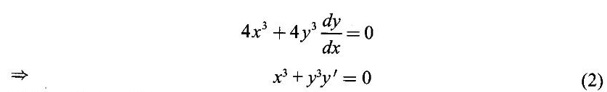
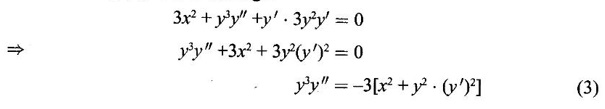
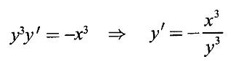

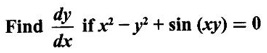
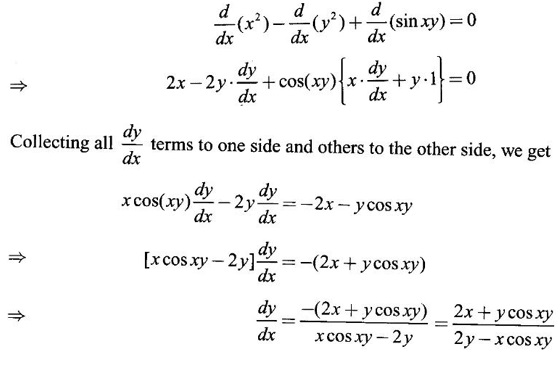
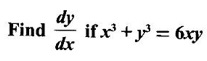
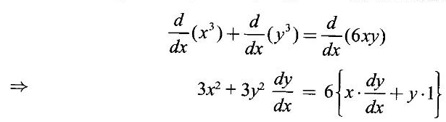
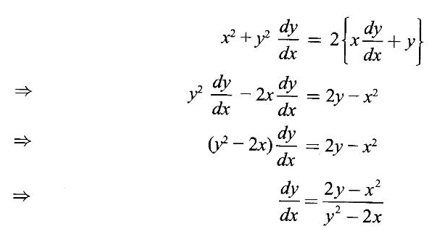


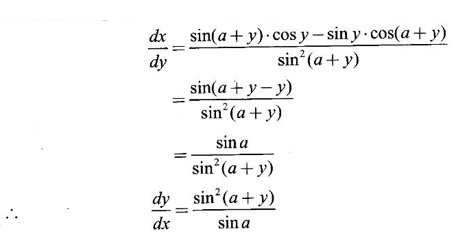

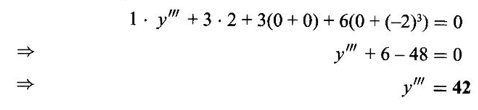
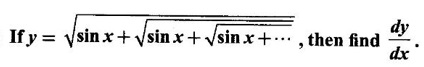
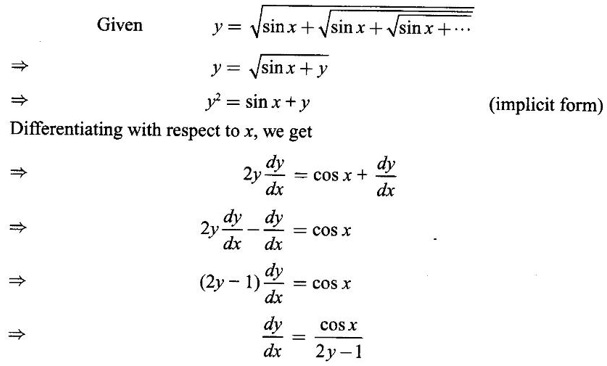
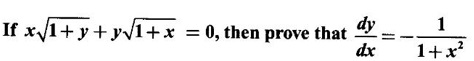
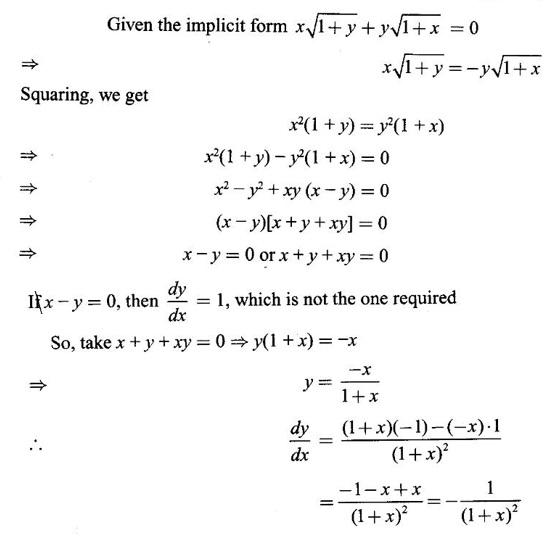
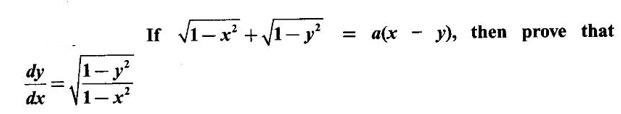

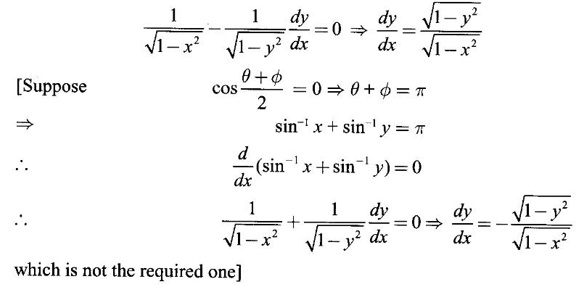
Matrices and Calculus: Unit II: Differential Calculus : Tag: : Worked Examples | Differential Calculus - Implicit Differentiation
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
