Matrices and Calculus: Unit II: Differential Calculus
Hyperbolic Functions
Definition, Worked Examples, Exercise with Answers | Differential Calculus
Certain combinations of exponential functions ex and e-x are called hyperbolic functions. They occur frequently in mathematical and engineering applications.
HYPERBOLIC FUNCTIONS Certain combinations of exponential functions ex and e-x are called hyperbolic functions. They occur frequently in mathematical and engineering applications. We have The odd combination is called hyperbolic sine of x and the even combination is called hyperbolic cosine of x using these two functions we define other hyperbolic functions. The prefix hyperbolic is due to the fact that (cos hθ, sin hθ) is a point on the hyperbola x2 - y2 = 1, much the same way as (cos θ, sin θ ) is a point on the circle x2 - y2 = 1. The hyperbolic functions possess many properties that resemble those of trigonometric functions. These identities can be verified using the definitions Proof: Similarly, we can prove others We saw inverse trigonometric functions exist in the restricted domains. Similarly, inverse hyperbolic functions exist Since hyperbolic functions are defined in terms of ex, the inverse hyperbolic functions can be expressed in terms of natural logarithms. Proof: Let y = sinh -1 x. Then sin y = x Similarly, we can prove the other inverse hyperbolic functions Proof: Similarly, we can prove the following Formulae Derivatives of hyperbolic functions Derivative of inverse hyperbolic functions Example 1 Find the derivative of f(x) = tanh(1 + e2x) Solution Example 2 Find derivative of tan h-1(sin x) Solution Let y = tan h-1(sin x) Example 3 Solution Example 4 Solution Given I. Rewrite the expressions in terms of exponential and find the derivatives II. Find the derivative of the following problems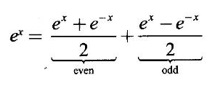
Definition 2.19

1. Hyperbolic Identities
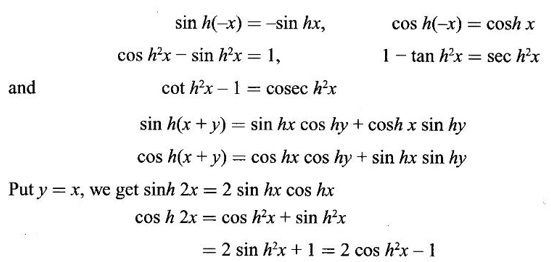
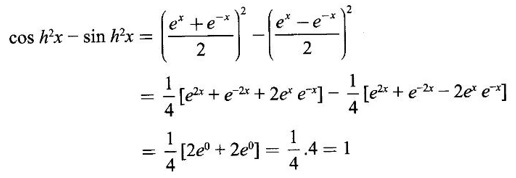
2. Derivatives of Hyperbolic Functions
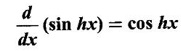
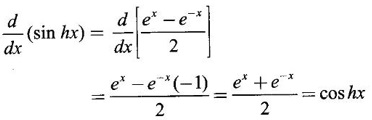
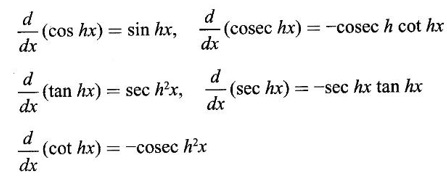
3. Inverse Hyperbolic Functions
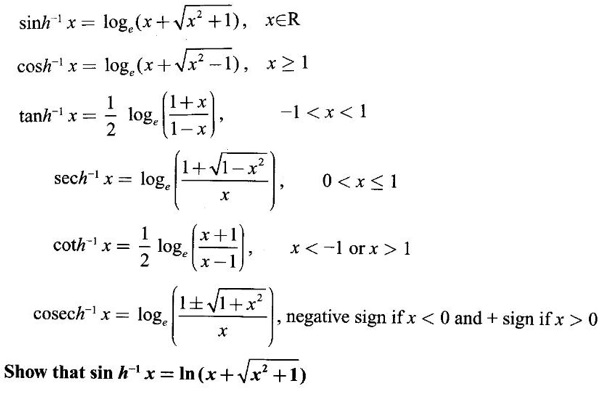

4. Derivatives of Inverse Hyperbolic Functions
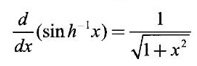
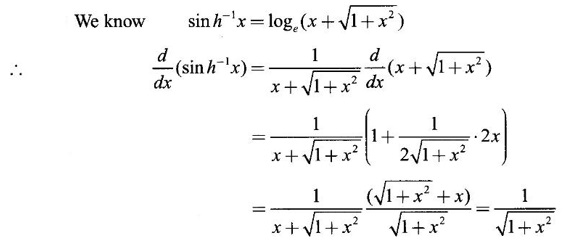
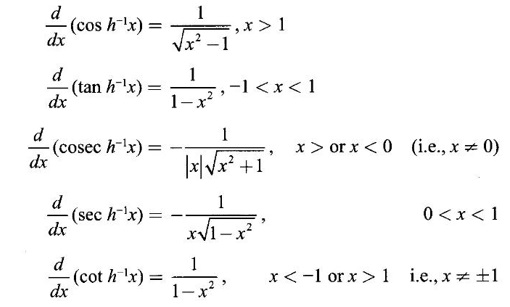
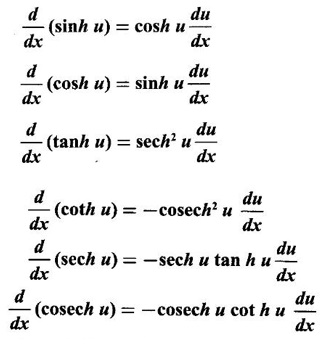
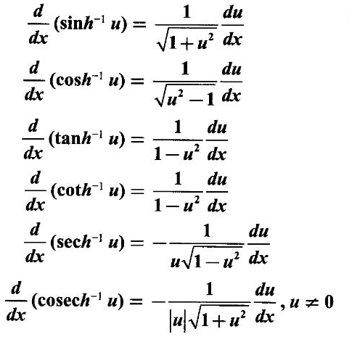
WORKED EXAMPLES
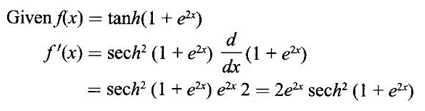
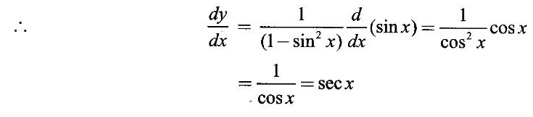
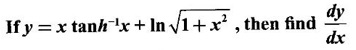
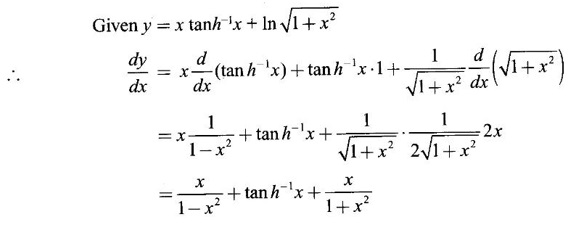
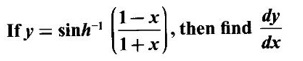

EXERCISE 2.9

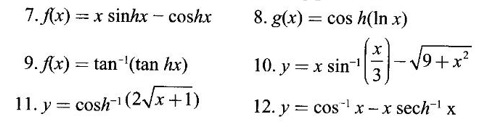
ANSWERS TO EXERCISE 2.9
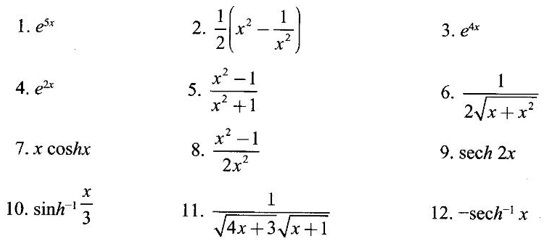
Matrices and Calculus: Unit II: Differential Calculus : Tag: : Definition, Worked Examples, Exercise with Answers | Differential Calculus - Hyperbolic Functions
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
