Engineering Physics: Unit V: Applied Quantum Mechanics
Harmonic Oscillator (Qualitative)
Definition, Examples, Formula, Wave equations, Wave functions
A particle undergoing simple harmonic motion is called a harmonic oscillator.
HARMONIC OSCILLATOR (Qualitative) Definition A particle undergoing simple harmonic motion is called a harmonic oscillator. In harmonic oscillator, the force applied is directly proportional to the displacement and is always directed towards the mean position. Examples. Familiar examples are; a simple pendulum, an object floating in a liquid, a diatomic molecule and an atom in a crystal lattice. If applied force moves the particle through x, then restoring force F is given by The potential energy of the oscillator is where k is force constant. In harmonic oscillator, angular frequency is given by Squaring on both sides where m - mass of the particle Substituting k in eqn (1), we have The time - independent Schrodinger wave equation for linear motion of a particle along the x-axis is: where E – Total energy of the particle, V - Potential energy and Ψ - Wave-function for the particle which is function of x alone. Substituting for V in equation (4) we get: This is Schrodinger wave equation for the oscillator. To simplify eqn. (6), a dimensionless independent variable y is introduced. It is related to x by the equation y = ax ... (7) Now we have Differentiating Substituting for a2 The wave equation for the oscillator is satisfied only for discrete values of total energies given by where, n = 0, 1, 2, ......, and v is the frequency of the classical harmonic oscillator, given by From eqn. (13),we get the following conclusions: 1. The lowest energy of the oscillator is obtained by putting n = 0 in eqns (12) and (13) it is: This is called the ground state energy or the zero point vibrational energy of the harmonic oscillator. The zero-point energy is the characteristic result of quantum mechanics. The values of En in terms of E0 are given by: where n = 0, 1, 2, 3, ... 2. The eigen-values of the total energy depend only on one quantum number n. Therefore all the energy-levels of the oscillator are non-degenerate. 3. The successive energy-levels are equally spaced; the separation between two adjacent energy-levels being In the figure 7.2 the horizontal lines show the energy levels and the dashed curve is parabola representing the potential energy V = 1/2 kx2 For each value of the parameter (i) the normalization constant Nn given by: (ii) the exponential factor (iii) a polynomial Hn (y), called Hermite polynomial in either odd or even powers of y. Thus the general formula for the nth wave function is: The first six Hermite polynomials are given in the following table: For lowest (ground) state, n = 0 This is the lowest value of energy, called zero point energy. Even if the temperature reduces to absolute zero, the oscillator would still have an amount of energy 1/2 hv. In old quantum mechanics, the energy of nth level... whereas in wave mechanics A comparison of two results shows that the only difference in old quantum mechanics and wave mechanics is that all the equally spaced energy levels are shifted upward by an amount equal to half the separation of energy levels i.e., 1/2 hv (equal to zero point zero). The existence of zero point energy is an important feature of wave mechanics and has been found to be experimentally true. • Experiments in scattering of light by crystals at low temperature show that when temperature is decreased, the intensity of scattered light tends to a finite limit and remains unchanged with further decrease in temperature. • It indicates that the oscillations of the atom in the crystal do not stop even at absolute zero.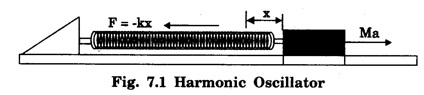

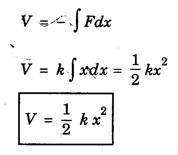
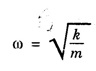
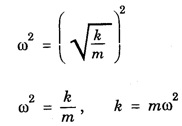
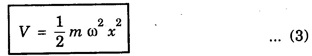
Wave equations for the oscillator
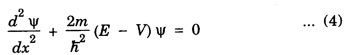
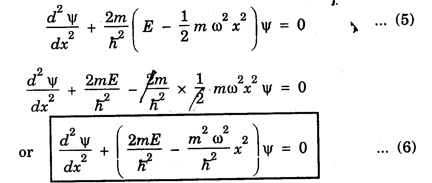
Simplification of the wave equation
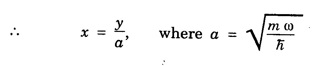
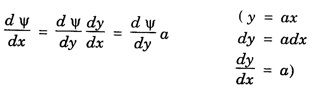

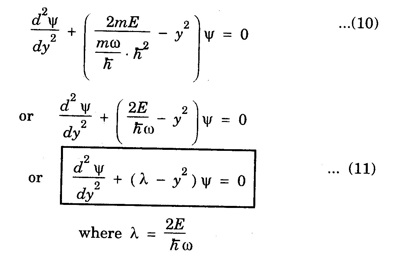
Eigen-values of the total energy En
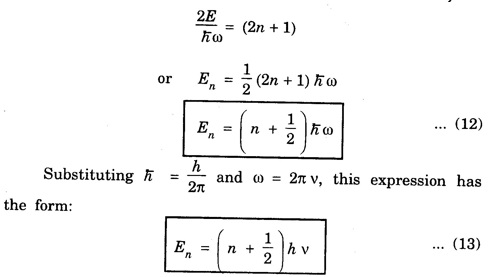
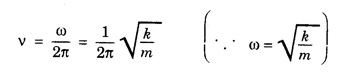
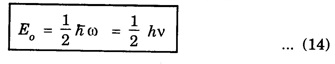

 The energy-level diagram for the harmonic oscillator is shown in fig. 7.2.
The energy-level diagram for the harmonic oscillator is shown in fig. 7.2.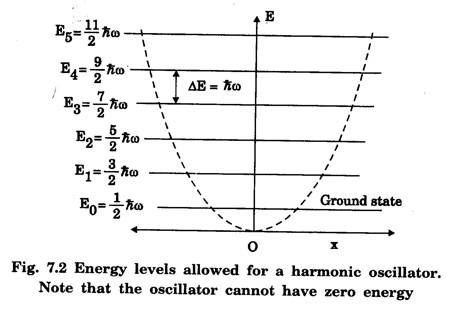
Wave functions of the harmonic oscillator
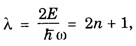 there is a different wave function Ψn, which consists of:
there is a different wave function Ψn, which consists of: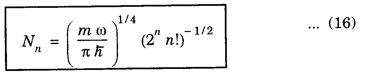
![]() and
and 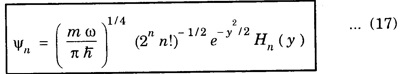

Significance of zero point energy
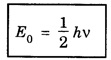
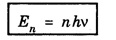

Engineering Physics: Unit V: Applied Quantum Mechanics : Tag: : Definition, Examples, Formula, Wave equations, Wave functions - Harmonic Oscillator (Qualitative)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
