Matrices and Calculus: Unit II: Differential Calculus
Geometrical Interpretation of Derivative
Worked Examples, Exercise with Answers | Differential Calculus
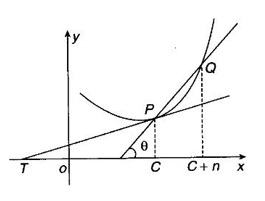
The derivative f'(c) of a function ƒ at a point c is the slope of the tangent at the point (c, f(c)) on the graph of ƒ given by the equation y = f(x).
GEOMETRICAL INTERPRETATION OF DERIVATIVE The derivative f'(c) of a function ƒ at a point c is the slope of the tangent at the point (c, f(c)) on the graph of ƒ given by the equation y = f(x). Let ƒ be a differentiable function on [a, b]. The graph of ƒ is the set {(x, y)|y = f(x), x ∈ [a, b]} . That is y = f(x) is the equation of the graph of ƒ, Let c, c + h ∈ [a,b]. So, that P(c, f(c)) and Q(c+h, f(c+h)) be the corresponding points of the curve y = f(x). Then the slope of the chord Suppose the point Q moves along the curve towards P, then the chord PQ approaches to a definite line PT in the limit as Q→ P. This line PT is called the tangent line to the curve at P. So, when f'(c) exists, it is the slope of the tangent PT at P. ⸫ the equation of the tangent at P is. y = ƒ(c)= ƒ'(c)(x - c). 1. The equation of the tangent at (x1, y1) The given curve is y = f(x). Let P(x1, y1) be any point on the curve. Let m be the slope of the tangent at (x1, y1). ⸫ the equation of the tangent at P(x1, y1) is y - y1 = m(x - x1 ). 2. The equation of the normal at (x1, y1) The normal at P(x1, y1) is a straight line through P and perpendicular to the tangent at P. Note: The derivative f'(c) of ƒ at c is defined as a real number. However, for geometrical convenience, we extend the definition to include ± ∞. We define f'(c) = ∞, if f'(c-) = ∞ and f'(c+) = ∞ and f'(c) = -∞, if ƒ'(c-) = -∞ and ƒ'(c+) = -∞. Thus, if dy/dx = 0, the tangent is parallel to the x-axis. Example 1 Find the equations of the tangent and normal line to the curve Solution Example 2 If F(x) = Solution ⸫ the equation of the normal at the point (2, 2) y - y1 = m1 (x - x1) Example 3 Find the points on the curve y = x4 - 6x + 4, where the tangent is horizontal. Solution Let (x1, y1) be a point on y = x4 - 6x + 4 (1) where tangent is horizontal ⸫ tangent is parallel to the x-axis Differentiating (1) with respect to x, we get Example 4 Find the points on the curve y = x4 - 6x3 + 13x2 - 10x + 5 where the tangents are parallel to the line y = 2x and prove that two of the points have the same tangent. Solution The given curve is y = x4 - 6x3 + 13x2 - 10x + 5 (1) Let the tangent at the point (x1, y1) on the curve be parallel to the line y = 2x. ⸫ the slope of the tangent at the point (x1, y1) = The slope of the line y = 2x. Since the slope of the line = 2, the slope of the tangent is 2. Differentiating (1) w.r.to x, we have By inspection x1 = 1 is a root. The other roots are given by At these points the tangents to the curve are parallel to the line y = 2x. Now we have to prove that at two of these points, the tangents are same. At the point (1,3) The equation of the tangent is y – 3 = 2(x - 1) ⇒ y – 3 = 2x – 2 ⇒ 2x – y + 1 = 0 (2) At the point (2,5) The equation of the tangent is y – 5 = 2(x - 2) ⇒ y – 5 = 2x – 4 ⇒ 2x – y + 1 = 0 (3) The equations (2) and (3) are the same. ⸫ the tangents at the points (1,3), (2,5) are the same. Example 5 Find the equations of the tangents from the origin to the curve y = 4x3 - 2x5. Solution The given curve is y = 4x3 - 2x5. (1) Let a tangent from the origin to the curve touch the curve (1) at the point P(x1, y1). ⸫ OP is a tangent to the curve and y1 = 4x13 - 2x15 (2) ⸫ the points of contact of the tangents from the origin to the curve are (1, 2) and (−1, − 2) . At the point (1, 2): The slope of the tangent is m = ⸫ the equation of the tangent is y – 2 = 2(x - 1) ⇒ y = 2x. At the point (-1,−2): The slope of the tangent is ⸫ the equation of the tangent is y - (-2) = 2(x − (−1)) ⇒ y + 2 = 2(x + 1) ⇒ y = 2x. So, from the origin, same tangent is drawn to the curve. See Fig. above. Example 6 Find the equation of the normal line to the parabola y = x2 - 5x + 4 that is parallel to the line x - 3y = 5. Solution Given curve is y = x2 - 5x + 4. Let (x1, y1) be a point on the curve at which the normal is parallel to x - 3y = 5. Example 7 Find the equations of the tangent at any point P on y2 = x3. If the tangent at P meets the curve again at Q and the lines OP and OQ (O is the origin) make angles α, β with the x-axis, then prove that tan α = -2 tan β. Solution The given curve is Given that OP and OQ make angles α and β with the x-axis. ⇒ t = -2 tan β tan α = -2 tan β. Example 8 Find a cubic function f(x) = ax3 + bx2 + cx + d whose graph y = ax3 + bx2 + cx + d has horizontal tangents at the points (−2, 6) and (2, 0). Solution Given curve is y = ax3 + bx2 + cx + d. The points (-2, 6) and (2, 0) are points on the curve. So, they satisfy the equation of the curve Example 9 Show that the portion of the tangent at any point on the curve Solution Let (a cos3θ, a sin3θ) be any point on the curve If the tangent meets the coordinate users at A and B, the x-intercept OA = a cos θ y-intercept OB = a sin θ which is a constant Example 10 Show that the curve y = 6x3 + 5x – 3 has no tangent line with slope 4. Solution The given curve is y = 6x3 + 5x – 3 Differentiating w.r. to x, we get Suppose (x1, y1) is the point on the curve at which the tangent has slope 4 The slope the tangent at the point (x1, y1) is ⸫ there is no tangent to the curve with slope 4. Example 11 Find the values of a and b if the line 2x + y = b is a tangent to the parabola y = ax2 when x = 2. Solution The given curve is y = ax2 (1) Also given that the line 2x + y = b (2) tangent to the curve when x = 2 Example 12 If c > 1/2, how many lines through the point (0, c) are normal to y = x2? What happens if c ≤ 1/2? Solution Let p(t, t2) be a point on the parabola so that the normal at the point passes through (0, c). Differentiating (1) w.r. to x, we get ⸫ t2 > 0, which will give two real values for t, say t1 and t2. ⸫ t = 0, t1, t2 are real, correspondingly we get three normal to the curve through (0, c) ⸫ t is immaginary and t = 0 is the only real value So, there is only one normal through(0, c), which is the y-axis for t = 0 ⸫ the point is (0, 0), the origin and the normal is the y-axis 1. Find the equation of tangents to the curve y = (x3- 1)(x - 2) at the point where it meets the x-axis. 2. Find the equation of the tangents from the origin to the curve y = 2x2 + 1 3. Find the equation of normal to the curve 3x2 - y2 = 8 which is parallel to the line x + 3y = 4. 4. Find the equation of the tangent to the curve y = 7x - x2 at the point (3, 12) on it. Also find the equation of the normal at the point. 5. Find the points on the curve y2 = 2x(3 - x2) at which the tangents are parallel to the x-axis. 6. Find the points on the curve y3 = x2(2a - x), where the tangents are parallel to y-axis. 7. If the tangent at (x1, y1) on the curve y3 + x3 – 9xy + 1 = 0 is parallel to the x-axis, prove that at the point 8. Find the equation of the tangent to the curve x = 9. Find the abscissa of the point on the curve ay2 = x3 at which the normal cuts off equal intercepts on the coordinate axes. [Hint: A line makes équal intercepts if its slope = 1 or -1]. 10. If the tangent at (1, 3) on the parabola y = 4x – x2 cuts the parabola y = x2 - 6x + k at two different points, find the values of k. 11. Find the equation of the tangent to the curve x2 + 4y2 =16 at the point which is such that it is the mid point of the portion of the tangent intercepted between the coordinate axes. 12. Find the points on x2 = y3 at which the normal pass through (0, 4). 13. The curve y = a x2 + bx + c passes through the points (-1, 0) and (0, -2). The tangent to the curve at the latter point makes 135° with the x-axis. 14. If p, q are the lengths of the perpendiculars from the origin to the tangent and normal at a point on x2/3+ y2/3 = a2/3, then prove that 4p2 + q2 = a2 15. Find the equation of the straight line which is tangent at one point and normal at another point of the curve x = 3t, y = 2t3. 16. Find all the tangents to the curve y = cos (x + y), -2π ≤ x ≤ 2π, that are parallel to the line x + 2y = 0. 17. Find the equation of the tangent and the normal to the curve 18. Find the equation of the tangent and the normal to the curve y(x - 2)(x - 3) – x + 7 = 0 at the point where it cuts the x-axis. 19. Prove that the line 20. Find a curve y = ax2 + bx + c that has slope 4 at x = 1, slope -8 at x = -1, and passes through the point (2, 15) 21. The curve y = ax3 + bx2 + cx + 5 touches the x-axis at p(-2, 0) and cuts the y-axis at a point Q where the gradient is 3. Find a, b, c1. Geometrical Interpretation of Derivative

2. Equation of the Tangent and the Normal to the Curve y = f(x)

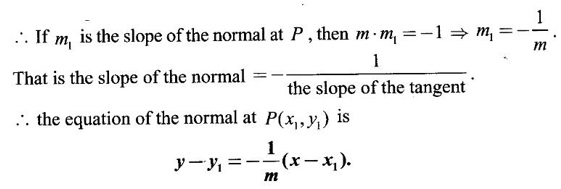
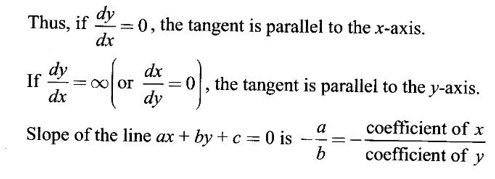
WORKED EXAMPLES
 at the point (3,2)
at the point (3,2)
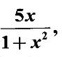 then find F '(2) and use it to find the equations of the tangent and normal to the curve
then find F '(2) and use it to find the equations of the tangent and normal to the curve

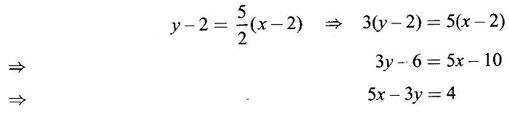
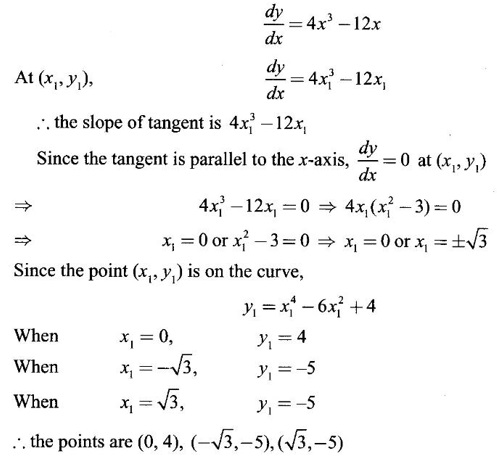
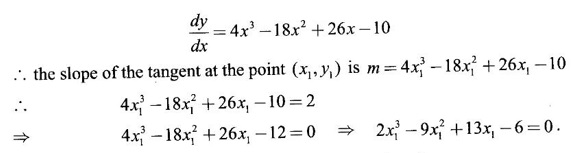
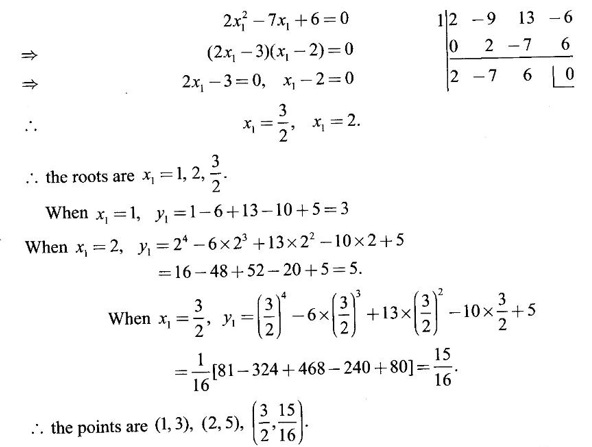

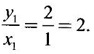



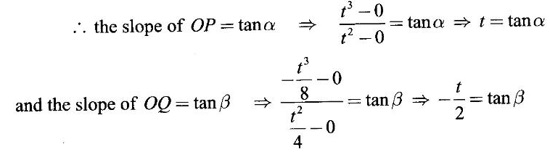

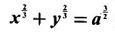 intercepted between the axis is a constant.
intercepted between the axis is a constant.
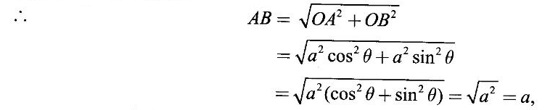

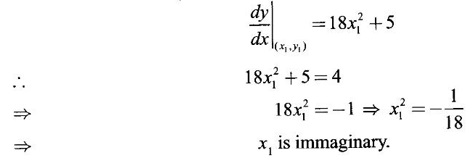





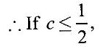 there is only one normal.
there is only one normal.EXERCISE 2.10

 at the point t = 2.
at the point t = 2. 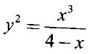 at the point (2, −2).
at the point (2, −2).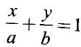 touches the curve y = be-x/a at the point where the curve crosses the y-axis.
touches the curve y = be-x/a at the point where the curve crosses the y-axis.ANSWERS TO EXERCISE 2.10
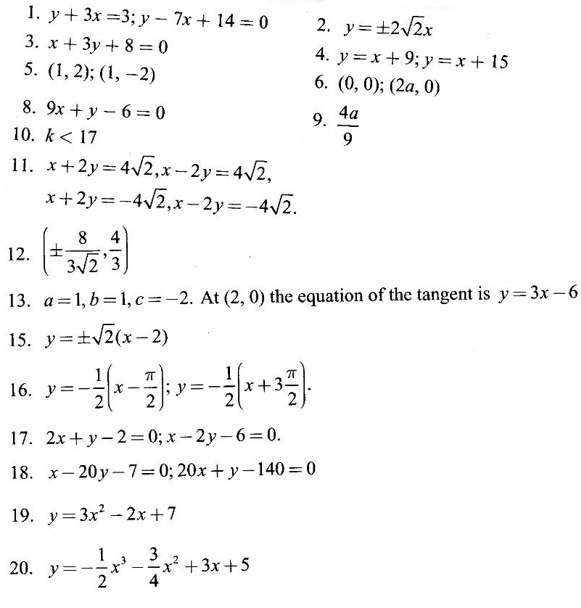
Matrices and Calculus: Unit II: Differential Calculus : Tag: : Worked Examples, Exercise with Answers | Differential Calculus - Geometrical Interpretation of Derivative
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
