Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies
General Procedure to Find Resultant of Non-concurrent Force System
with Solved Example Problems
Find magnitude and direction of resultant force using rectangular components :
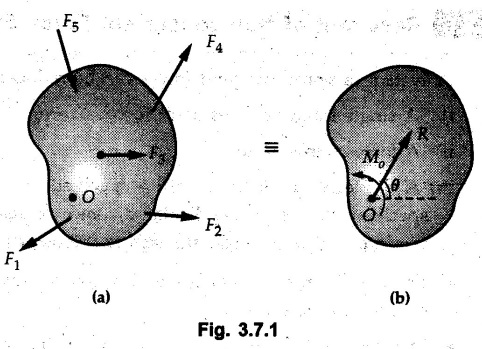
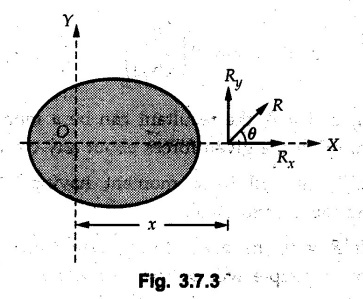
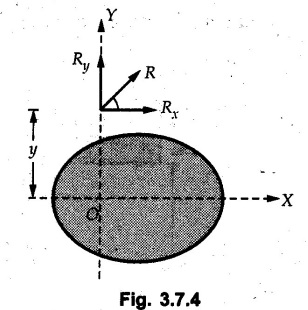
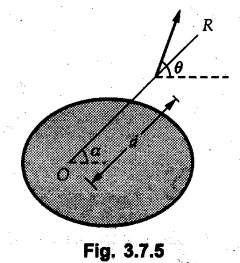
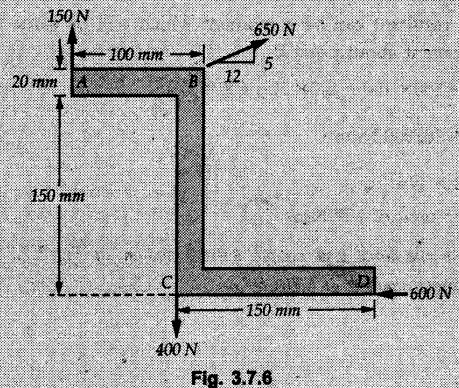
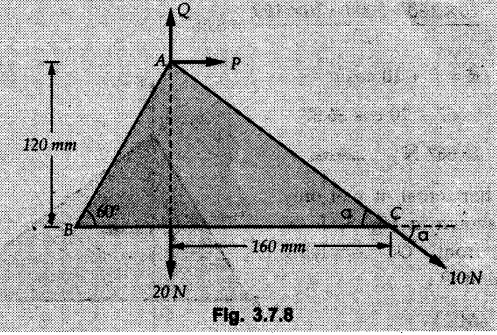
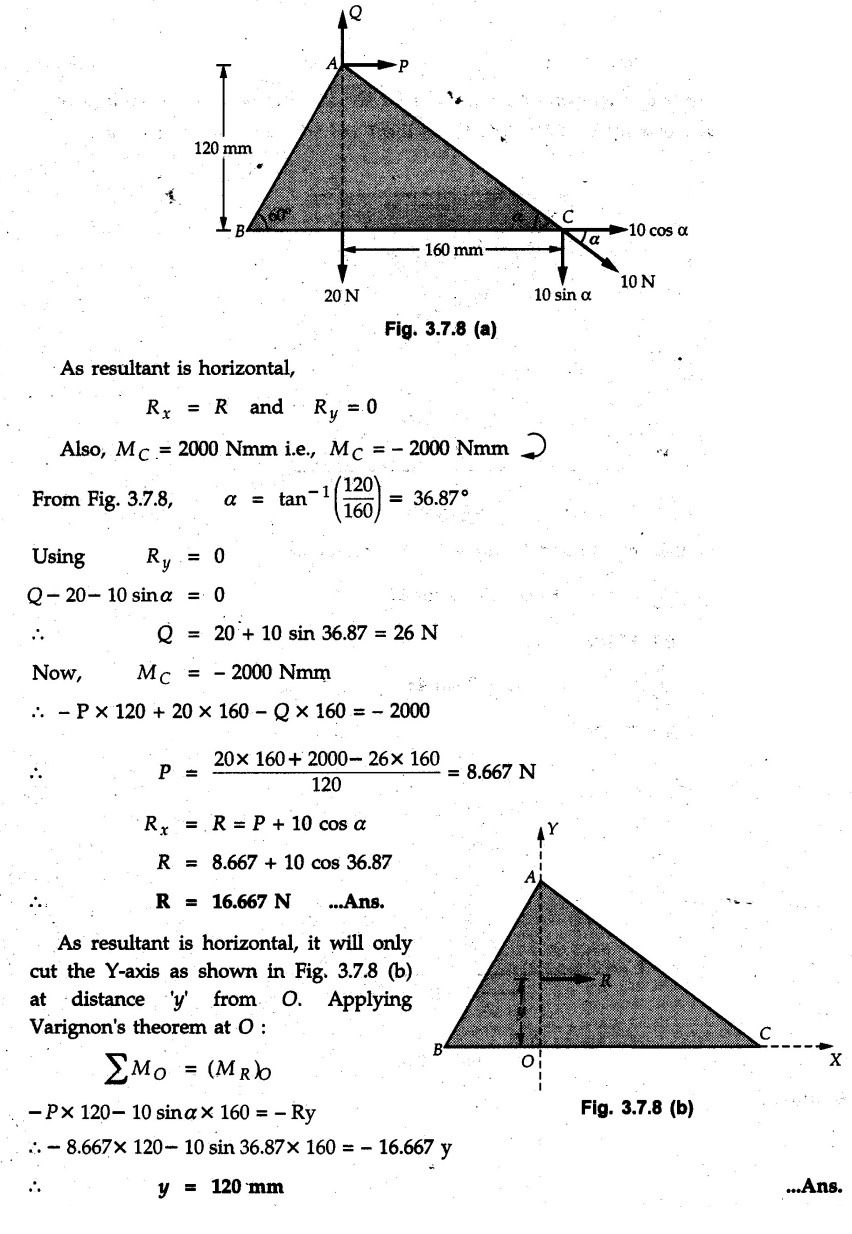
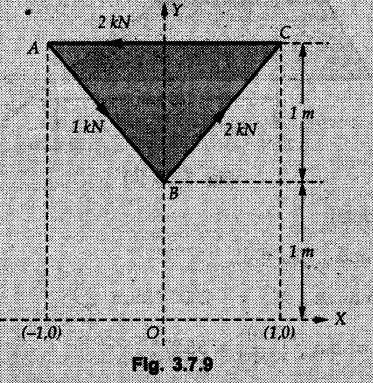
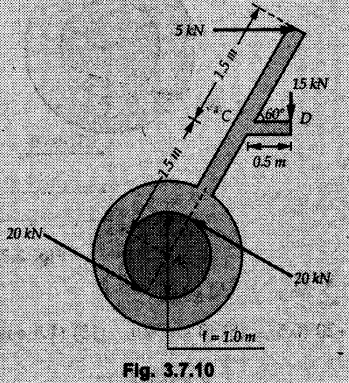
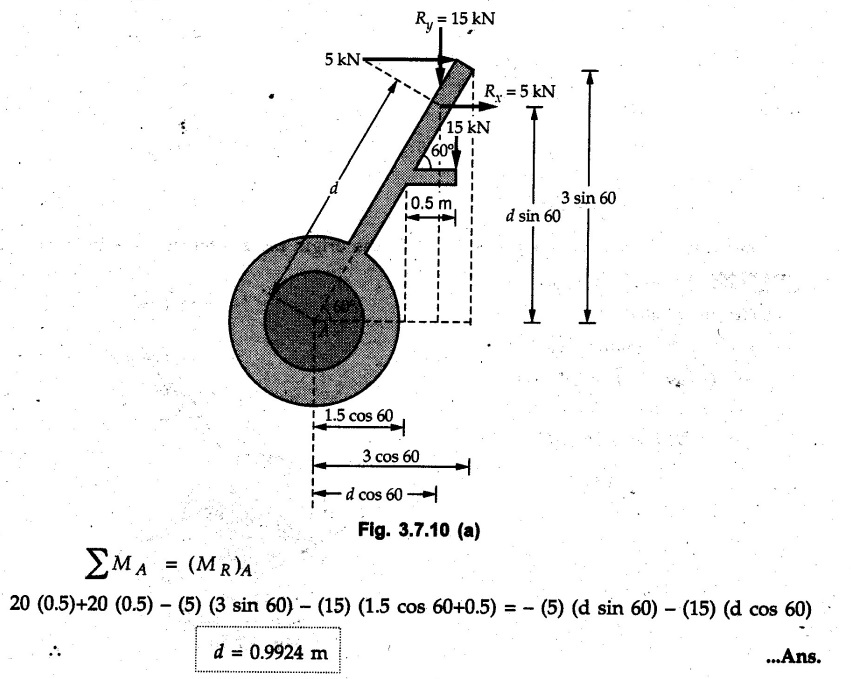
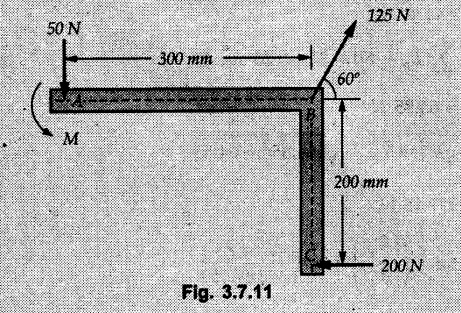
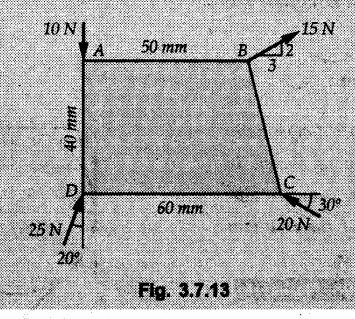
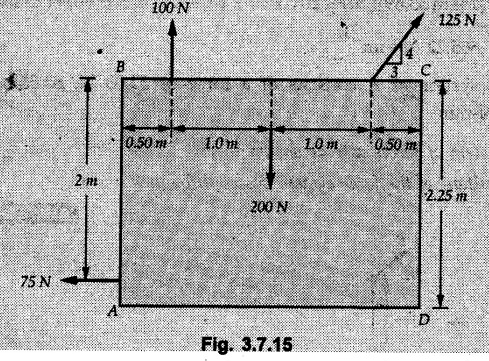
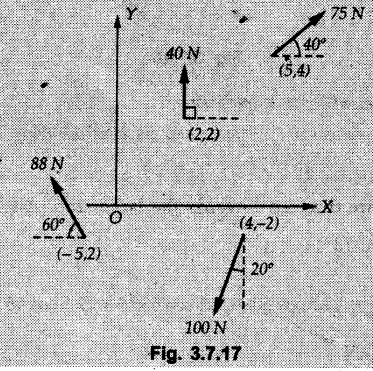
General Procedure to Find Resultant of Non-concurrent Force System I) Find magnitude and direction of resultant force using rectangular components : II) a) If R = 0, the resultant can be a moment. Find this resultant moment by taking moment of all the given forces about any convenient point in the plane. Equilibrant will be a moment having same magnitude as resultant moment but opposite sense of rotation. b) If R ≠ 0, the given force system can be reduced to a force-couple system. The moment of couple will be the moment of all the given forces about some given point. Thus a force system can be reduced to a force-couple system as shown in Fig. 3.7.1. c) If R ≠ 0, the line of action of resultant force can be specified in the following three ways: i) Line of action as defined by perpendicular distance 'd' from a specifed point can be obtained using Varignon's theorem. F1 d1 + F2 d2 + ... = Rd ... (3.7.1) If L.H.S is positive (i.e total moment due to all forces is anticlockwise according to sign convention followed in this book), the value of d is also positive representing anticlockwise moment of resultant. A negative value of d will represent clockwise F1 moment of resultant. The resultant can then be represented on a sketch as shown in Fig. 3.7.2. ii) Line of action as defined by x or y intercept : To find x-intercept, plot the resultant obtained in step I on X-axis at a distance 'x' as shown in Fig. 3.7.3 and use Varignon's theorem about O: F1 d1 + F2 d2 + ... = Ryx The R.H.S. representing moment of resultant is written by resolving R. Moment of R is zero about O. Moment of Ry is Ryx with anticlockwise sense of rotation and hence taken positive. To find y-intercept, plot the resultant on Y-axis at a distance 'y' as shown in Fig. 3.7.4 and use Varignon's theorem about O: F1 d1 + F2 d2 + ... = -Rxy Here line of action of Ry passes through 'O' and hence its moment about O is zero. Moment of Rx is Rxy with clockwise sense of rotation and hence taken negative. iii) Line of action as defined by point of application of resultant force on any inclined line: Plot resultant on the inclined line at some distance 'd', as shown in Fig. 3.7.5 and use Varignon's theorem to determine 'd'. Example 3.7.1 A Z-shaped lamina of uniform width of 20 mm is subjected to four forces as shown in Fig. 3.7.6. Find equilibrant in magnitude and direction. Solution : To find equilibrant, we have to find resultant, When R = 0, the resultant can be a moment which will be same about any point in the plane. Taking moment about point B, MB = -150 × 100 + 400 × 20 – 600 × 170 = -109000 Nmm Example 3.7.2 Replace the force and couple system shown in Fig. 3.7.7 by an equivalent single force and single moment at point 'P'. Solution : Example 3.7.3 Four forces acting on a triangle ABC are shown in Fig. 3.7.8. The sum of moments of these forces at point. C is 2000 N-mm clockwise. If resultant of force system is in horizontal direction, find its magnitude and point of application. Solution: Example 3.7.4 Forces of magnitudes 1 kN, 2 kN and 2 kN act along the sides of a triangular frame ABC as shown in Fig. 3.7.9. Find the resultant and intersection on X and Y axis. Solution: The intersection on Y-axis is at 15.48 m below the origin i.e. Y-intercept is -15.48 m. Example 3.7.5 A machine part is subjected to forces as shown in Fig. 3.7.10. Find resultant of forces in magnitude and direction. Also locate the point where the resultant cuts the central line of bar AB. Solution: In this case, both forces of 20 kN will cancel each other so no need to consider them while calculating the resultant. Let the resultant act at a distance d as shown in Fig. 3.7.10 (a). Using Varignon's theorem at A, Example 3.7.6 The three forces as shown in Fig. 3.7.11 and a couple 'M' are applied to an angle bracket. Determine the moment of the couple 'M' if the line of action of the resultant of this force system is to pass through i) B, ii) C. Solution: i) If line of action of resultant passes through B, the moment of resultant about B will be zero. Using Varignon's theorem at B, Example 3.7.7 Four forces act tangentially to a circle of radius 2 m as shown in Fig 3.7.12. Find the magnitude, inclination and distance of the resultant from the centre of the circle. Solution: Let d be the perpendicular distance of resultant from the centre of the circle. Using Varignon's theorem, (120) (2) – (50) (2) — (80) (2) (30) (2) = (177.15) (d) The negative value of d indicates clockwise moment of resultant about the centre of the circle. Example 3.7.8 Replace the given system of forces acting on a plate ABCD shown in Fig. 3.7.13 by a force-couple system acting at the point A. Solution: For 15 N force at B, the angle with horizontal is tan-1 (2/3) = 33.69° Example 3.7.9 A system of forces acts as shown in Fig. 3.7.14. Find the magnitude of A and B so that the resultant of the force system passes through P and Q. Solution: As the resultant passes through P, Example 3.7.10 Find equilibrant of four forces acting on a plate shown in Fig. 3.7.15. Solution: As R = 0, the resultant can be a moment which will be same about any point in the plane. Taking moment about the point of application of the 125 N force, M = (200) (1) (100) (2)— (75) (2) ⸫ M = - 150 Example 3.7.11 Four tugboats are used to bring an ocean large ship to its pier. Each tugboat exerts a 22.5 kN force in the direction as shown in the Fig. 3.7.16. i) Determine the equivalent force-couple system at O. ii) Determine a single equivalent 120 force and its location along the longitudinal axis of Solution: All the forces are directed towards the large ship. Angle of second force with horizontal is tan-1 (4/3) = 53.13°. Example 3.7.12 Find the resultant completely for the coplanar force system shown in Fig. 3.7.17. Solution: The magnitude and direction of resultant force can be obtained using rectangular components. The perpendicular distance of R from O. which defines its line of action can be obtained using Varignon's theorem at O. - (75 còs 40) (4) + (75 sin 40) (5) + (40) (2) + (88 cos 60) (2) – (88 sin 60) (5) = (100 sin 20) (2) – (100 cos 20) (4) = (73.44) (d) ⸫ d = - 8.8 As d is negative, the moment of resultant about O is clockwise.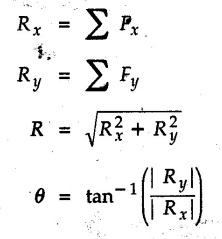

Solved Examples for Understanding

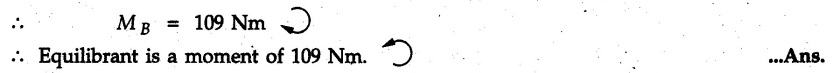
















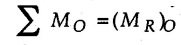
Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies : Tag: : with Solved Example Problems - General Procedure to Find Resultant of Non-concurrent Force System
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
