Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Gas Mixtures
Composition, Properties, Gibbs Function, Dalton's Law and Amagat's Law of Partial Pressure
Pure substance is defined as a substance which is homogeneous and not changing in its chemical composition.
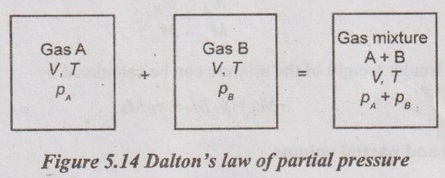
GAS MIXTURES Pure substance is defined as a substance which is homogeneous and not changing in its chemical composition. In many important thermodynamics applications, it requires homogeneous mixture of several pure substances rather than a single pure substance. Therefore, it is important to develop an understanding of mixtures and learn in handling them. A non-reacting gas mixture can be treated as a pure substance since it is usually a homogeneous mixture of different gases. The thermodynamic behaviour of a mixture of gases depends upon the individual properties of its constituent gases. Therefore, a wide variation is possible in the properties of gaseous mixtures. It is very important to know the composition of the mixture as well as the properties of the individual components to determine the properties of mixture. The following two ways are generally used to describe the composition of mixture. If a gas mixture consists of gases 1, 2, 3 and so on, the mass of the mixture is the sum of masses of individual component of the gases The mean fraction or mass fraction of any component is defined as the ratio of mass of a component (m1) to the mass of the mixture (mm). Mathematically, it can be written as In mass or gravimetric analysis, mass of each component is specified. Molar fraction is the ratio of the number of moles of a component (N1) to the total number of moles of the mixture (Nm). The total number of moles of a mixture is the sum of the number of its components. Then, the mole fraction is given by In molar analysis, moles of each component are specified. The number of moles N, mass m and molar mass M of a component and mixture are related by For example, a mixture consists of two gases having masses of mA and mB, the mole fraction of each gas is calculated by The sum of partial pressures of the components of a gas mixture is equal to the mixture pressure. The partial pressure pi of a component i in a gas mixture is given by Pi = yipm where yi = Mole fraction pm = Mixture pressure Σpi = Σyi pm = pm Σyi = pm This relation applies to any gas mixtures whether it is an ideal gas or not. The sum of partial volumes of the components of a gas mixture is equal to the volume of the mixture. The partial volume Vi of a component i in a gas mixture is given by Vi = yi Vm where Vm = Mixture volume ΣVi = ΣyiVm = Vm Σyi = Vm The partial volume is not the actual volume of a component as it exists in the mixture because each component fills the entire volume of the vessel that holds the mixture. According to Dalton's law of partial pressure, the total pressure exerted by a mixture of gases is equal to the sum of the partial pressures of the gases in the mixture, provided the gases do not react chemically with each other. This law is also called Dalton's law of additive pressure. where pm = Mixture pressure p1, p2, ... pi = Each component pressure If there are NA moles of gas A, NB moles of gas B and Nc moles of gas C in the mixture, the gas equation is given by pA (NA, Tm, Vm) is the pressure of NA moles of component A at the temperature Tm and volume Vm. For ideal gas, pi and Vi can be released to yi by using the ideal gas relation for both components and gas mixture According to Amagat's law of partial volumes, the volume of a gas mixture is equal to the sum of the volume of each gas if each gas is existed alone at the temperature and pressure of the mixture. The various properties of gas mixture such as pressure, volume, temperature, internal energy, enthalpy, entropy and special heats are discussed here. (i) Pressure: Using Dalton's law of partial pressure, the pressure of a mixture is the sum of pressure of each component at the temperature and volume of the mixture. (ii) Volume: Using Amagat's law of partial volumes, the volume of mixture is the sum of volume of each component at the temperature and pressure of the mixture. (iii) Temperature: At any uniform mixture, the temperature is same for each component of the mixture: Tm = TA = TB = TC (iv) Internal energy: For a mixture of ideal gases, the internal energy is given by Internal energy of a gas mixture per unit mass is given by (v) Enthalpy: For a mixture of ideal gases, enthalpy is given by Enthalpy for a gas mixture per unit mass is given by (vi) Specific heats: For a mixture of ideal gases, specific heats are given by (vii) Gas constant: (viii) Entropy: Gibbs theorem states that the total entropy of a mixture of gases is the sum of the partial entropies. By Gibbs functions, G = h - Ts dg = dh - d(Ts) = dh – Tds - sdT ... (5.132) We know that dh = Tds + vdp Substituting the value of dh in equation (5.132), so, dg becomes dg= Tds + vdp – Tds - sdT dg = vdp - sdT ….. (5.133)1. Composition of a Gas Mixture
1. Mass fraction


2. Molar fraction or Mole fraction

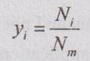
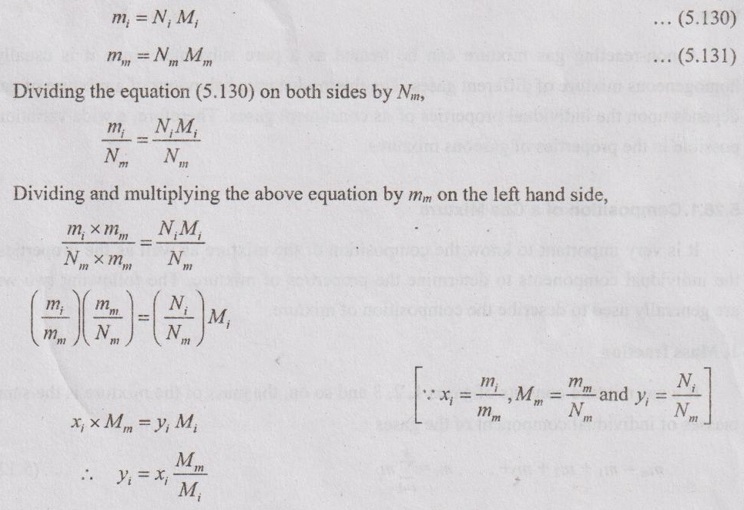
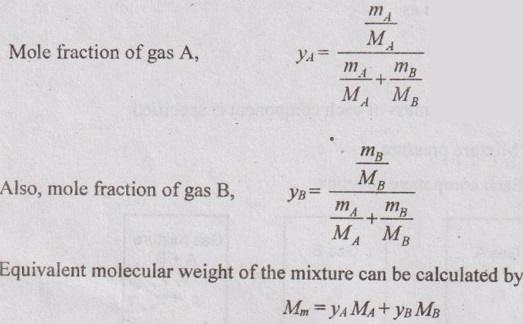
3. Partial pressure and partial volume
2. Dalton's Law of Partial Pressure

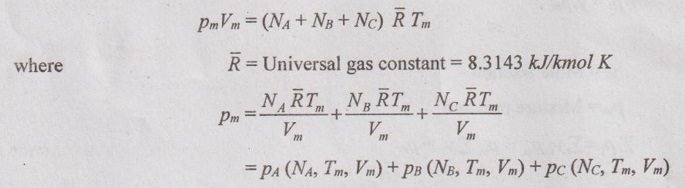

3. Amagat's Law of Partial Volume

4. Properties of Gas Mixtures


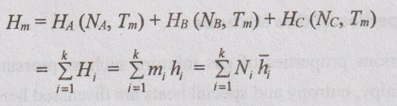



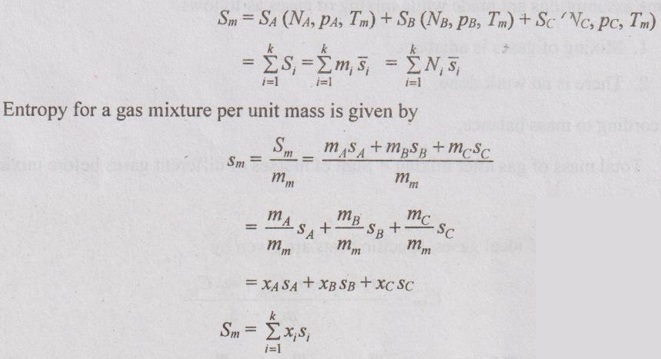
5. Gibbs Function
Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : Composition, Properties, Gibbs Function, Dalton's Law and Amagat's Law of Partial Pressure - Gas Mixtures
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
