Transforms and Partial Differential Equations: Unit IV: Fourier Transforms
Fourier Transform Pair
Definition, Properties, Proof Statement, Inversion formula, Parseval's identity, Convolution theorem, Solved Example Problems
Whatever definitions or format we use, there will be a difference in constant factor while finding F (s) = F [f(x)]. But this will be adjusted while expressing f(x) as a Fourier integral.
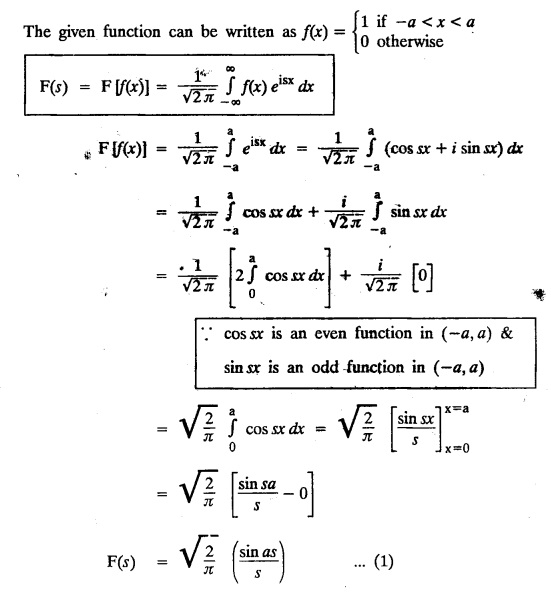
FOURIER TRANSFORM PAIR : a. Fourier Transform: [Complex Fourier Transform] Definition : The complex (or infinite) Fourier Transform The complex (or infinite) Fourier Transform of ƒ (x) is given by Then the function f(x) is the inverse Fourier Transform of F (s) and is given by The above (1) & (2) are jointly called Fourier transform pair. Note: Whatever definitions or format we use, there will be a difference in constant factor while finding F (s) = F [f(x)]. But this will be adjusted while expressing f(x) as a Fourier integral. For example, Let f(x) be a function satisfying Dirichlet's conditions in every finite interval (-l,l). Let F(s) denote the Fourier transform of f(x). Then at every point of continuity of f(x), we have Proof : By Fourier integral theorem, c. PROPERTIES OF FOURIER TRANSFORMS : 1. Linear property F [af(x)+bg(x)] = a F [f(x)] + b F [g(x)] where a and b are real numbers. Proof : 2. Change of scale property For any non-zero real Proof : Similarly if a < 0 Combining (1) & (2), we get 3. Shifting property (i) F [f(x − a)] = eias F (s) (ii) F [eiax f (x)] = F [s+a] Proof : (i) We know that, (ii) We know that, 4. Modulation Property : Modulation theorem : If F (s) is the Fourier transform of f(x), then F [f(x) cos ax] = 1/2 [F (s + a) + F (s − a)] Proof: We know that, 5. Proof : We know that, Differentiating both sides n times w.r.to s, we get 6. Proof : We know that, 7. Proof : 8. Proof: We know that, Taking complex conjugate on both sides 9. F [f(-x)] = F(-s) Proof: We know that, Definition: Convolution The convolution of two functions f(x) and g(x) is defined as The Fourier transform of the convolution of f(x) and g(x) is the product of their Fourier transforms. (i.e.,) F [f(x) * g (x) ] = F (s) G (s) = F [ƒ (x)] F [g (x)] Proof: by changing the order of integration, we get If F (s) is the Fourier transform of ƒ (x), then Proof : By convolution theorem, Note: In the same way, we can prove Parseval's identity for Fourier sine and cosine transforms. II. (a) Problems based on Fourier Transform [Complex Fourier Transform] Formula: Example 4.2.a(1) : Find the Fourier Transform of Solution: The given function can be written as Example 4.2.a(2): Find the Fourier Transform of Solution : The given function can be written as Example 4.2.a(3): Find the Fourier transform of f(x) given by Solution: The given function can be written as Definition: Self reciprocal : If a transformation of a function f(x) is equal to ƒ(s) then the function f(x) is called self reciprocal. Example 4.2.a(4): Show that the Fourier Transform of (OR) Show that Solution : Example 4.2.a(5): Find the Fourier transform of f(x) defined by Solution: Example 4.2.a(6) : Show that the Fourier transform of Solution: Given function can be written as Example 4.2.a(7) : Find the (complex) Fourier transform of Solution: Example 4.2.a(8): Find the Fourier transform of Solution: We know that, Example 4.2.a(9) : Find the Fourier transform of Solution: We know that, Example 4.2.a(10) : Find the Fourier transform of Solution: Example 4.2.a(11) Find the Fourier transform of Dirac delta function δ (t− a). Solution: The Dirac delta function is defined as The Fourier transform of δ (t - a) is Il.(b) Problems based on Fourier transform and its inversion formula Example 4.2.b(1) : Find the Fourier transform of the function f(x) defined by Hence, prove that Solution: The given function can be written as By Fourier inversion formula, we have Example 4.2.b(2) : Find the Fourier Transform of Solution: We know that, By inversion formula Note : Even function : If f (-x): f(x) in (−l,l) then f(x) is an even function. Odd function : If ƒ (-x) = -f(x) in (−l,l) then f(x) is an odd function In the above problem, a cos sx is an even function, a sin sx is an odd function |x| is an even function, |x| cos sx is an even function |x| sin sx is an odd function. Example 4.2.b(3): Find Fourier transform of e-a|x| and hence deduce that Solution: We know that, Using inversion formula, we get Example 4.2.b(4): Find the Fourier transform of e-|x| and hence find the Fourier transform of e-|x| cos 2x. Solution: To find : F [e-|x| cos 2x] By Modulation theorem, Il.(c) Problems based on inversion formula, Parseval's identity and Convolution theorem Example 4.2(1): Find the Fourier transform of Hence deduce that Solution : (i) Now, by Fourier inversion formula, we have (ii) Using Parseval's identity Example 4.2.c(2) Find the Fourier Transform of Solution: The Fourier transform of f(x) is Example 4.2.c(3): Show that the Fourier transform of Solution: (i) Using inverse Fourier Transform, we get Put x = 0, we get (ii) Using Parseval's identity, Example 4.2.c(4) : Find the Fourier transform of e-a|x| if a > 0 Deduce that Solution: Given : f(x) = e-a|x| See Example 4.2.b(3) in page no. 4.53 By Parseval's identity, If F(S) is the Fourier transform of f(x), then Example 4.2.c(5) Find the Fourier transform of Solution: See Example 4.2.b(1) in page no. 4.48 for problems based on Fourier transform and its inversion formula Example 4.2.c(6) : Find the Fourier transform of f(x) given by Solution : The given equation can be written as f(x) = 1 if -2 < x < 2 = 0 otherwise F (s) = F [f(x)] (i) Now, by Fourier inversion formula, we have Example 4.2.c(7): Find the Fourier transform of e-|x|, using Parseval's identity show that Solution: Example 4.2.c(8): If f(x) = Solution: We know that, By Parseval's identity, Example 4.2.c(9) : Verify convolution theorem for Definition: Convolution theorem for Fourier transforms. The Fourier transform of the convolution of ƒ (x) and g(x) is the product of their Fourier transforms. F [f(x) *g(x)] = F {f(x)} F {g (x)} Hence, convolution theorem is verified.


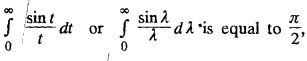 whatever definitions or format we use.
whatever definitions or format we use.b. INVERSION FORMULA FOR FOURIER TRANSFORM

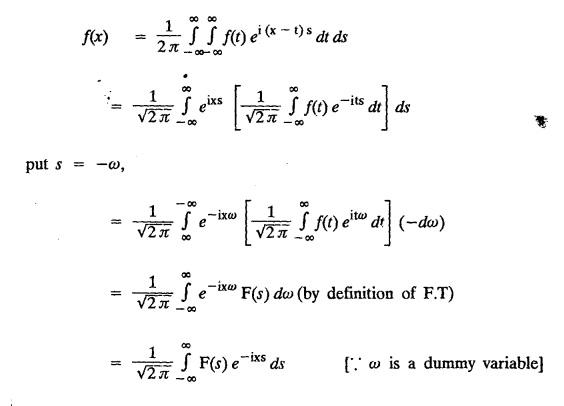
PROPERTIES - TRANSFORMS OF SIMPLE FUNCTIONS



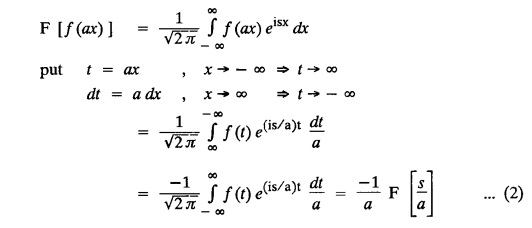
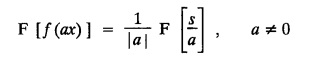



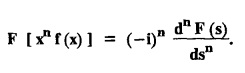
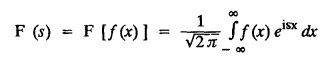

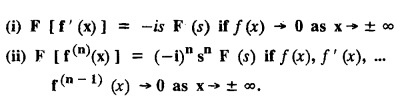



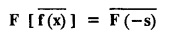



d. CONVOLUTION THEOREM PARSEVAL'S IDENTITY
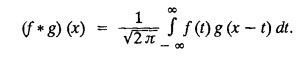
Convolution Theorem :

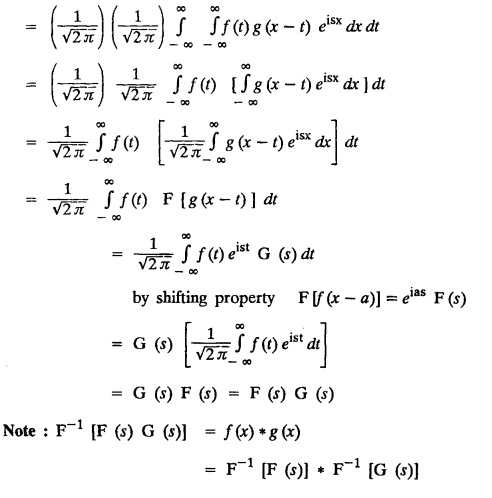
PARSEVAL'S IDENTITY:

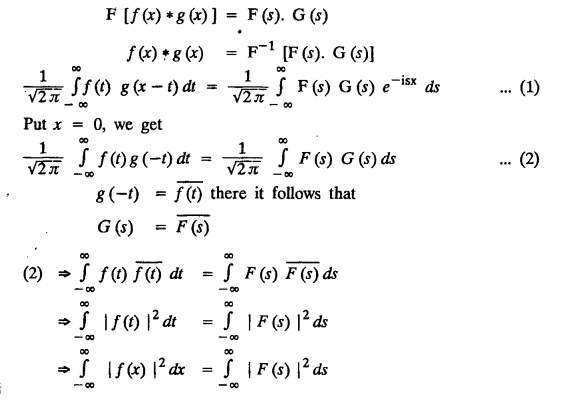
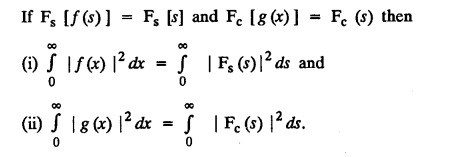





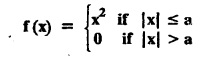


![]() is self-reciprocal with respect to Fourier Transform.
is self-reciprocal with respect to Fourier Transform.
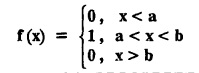

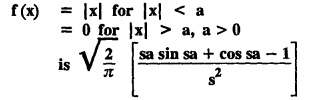


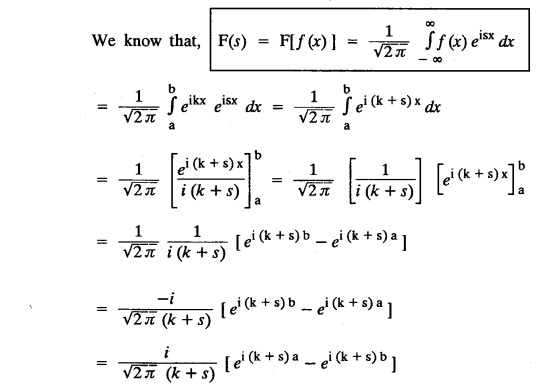
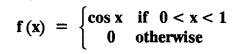

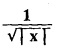

 Hence, show that
Hence, show that  is self reciprocal under Fourier transform.
is self reciprocal under Fourier transform.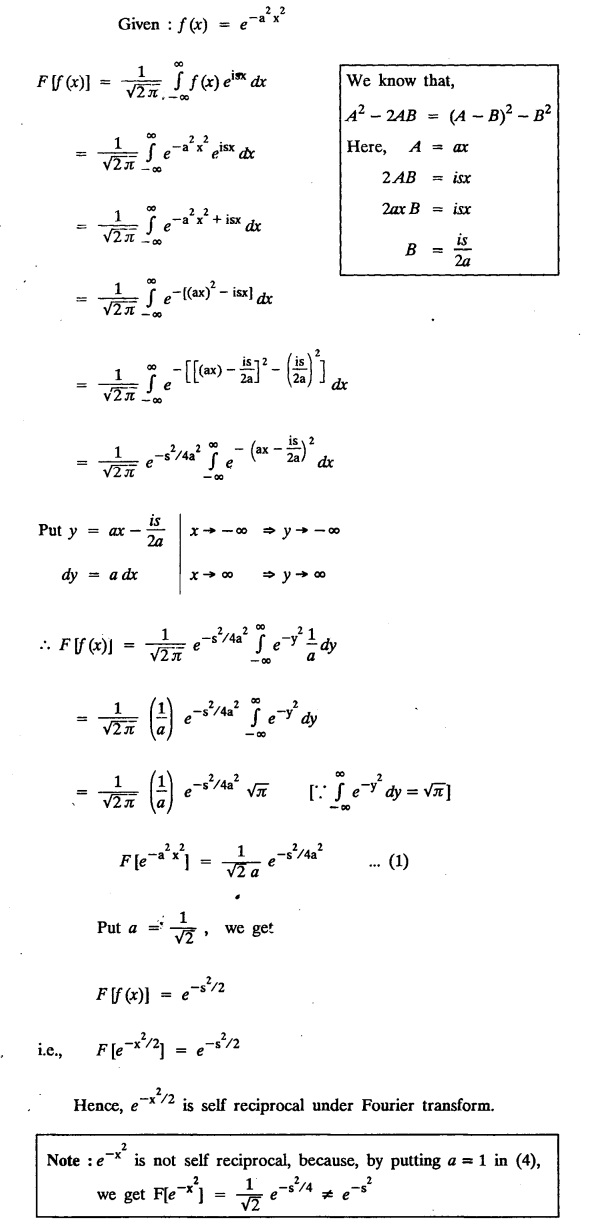
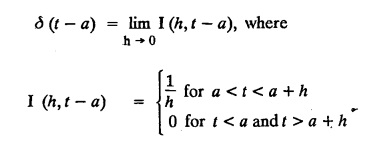

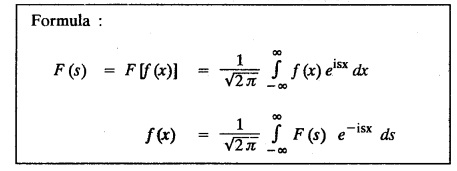






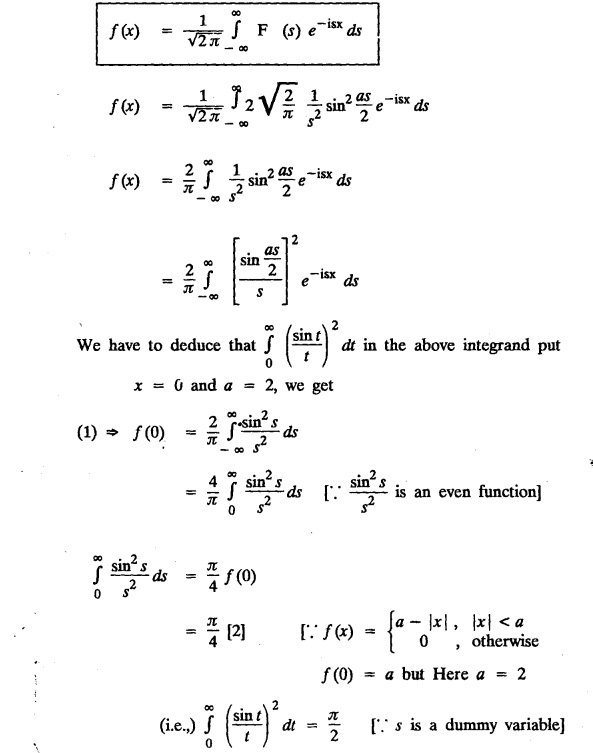
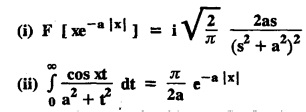



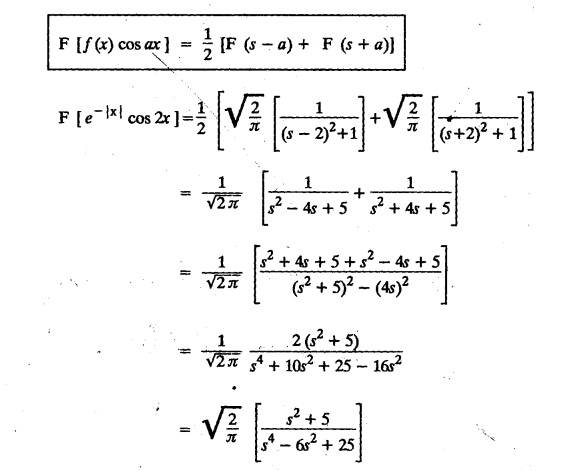

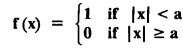 where a is a positive real number.
where a is a positive real number.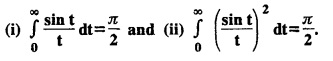



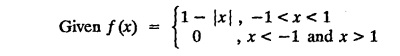





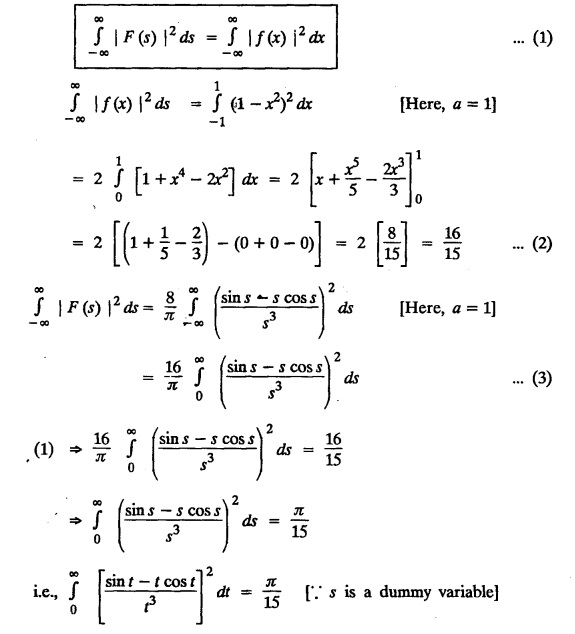
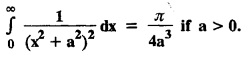

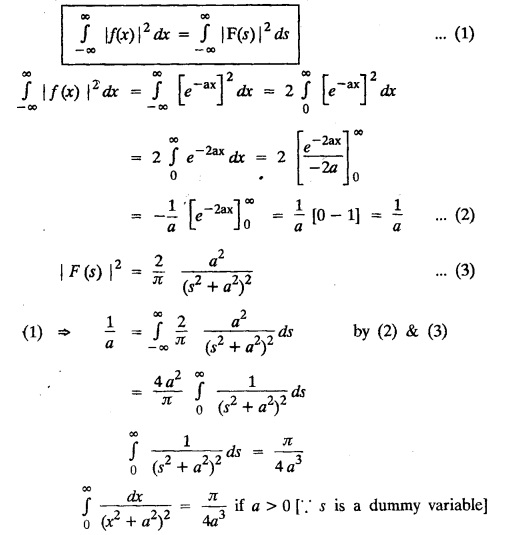

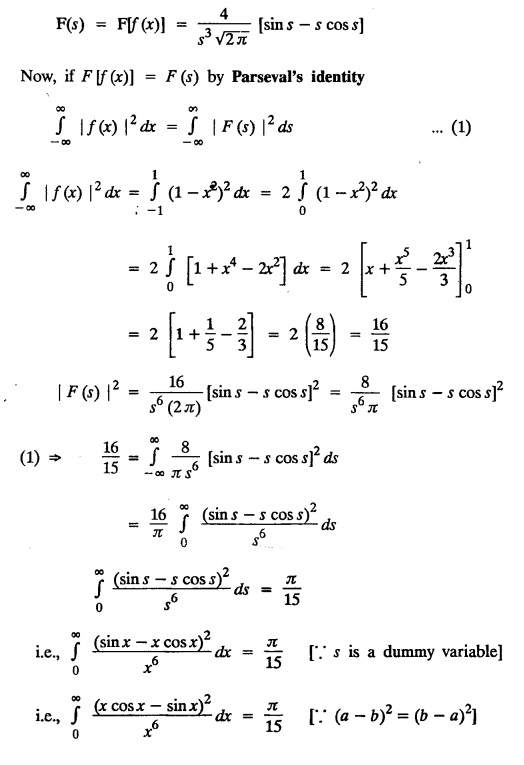





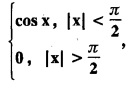 then find the Fourier transform of f (x) and hence, evaluate
then find the Fourier transform of f (x) and hence, evaluate 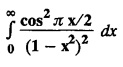 using Parseval's identity.
using Parseval's identity.



Transforms and Partial Differential Equations: Unit IV: Fourier Transforms : Tag: : Definition, Properties, Proof Statement, Inversion formula, Parseval's identity, Convolution theorem, Solved Example Problems - Fourier Transform Pair
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
