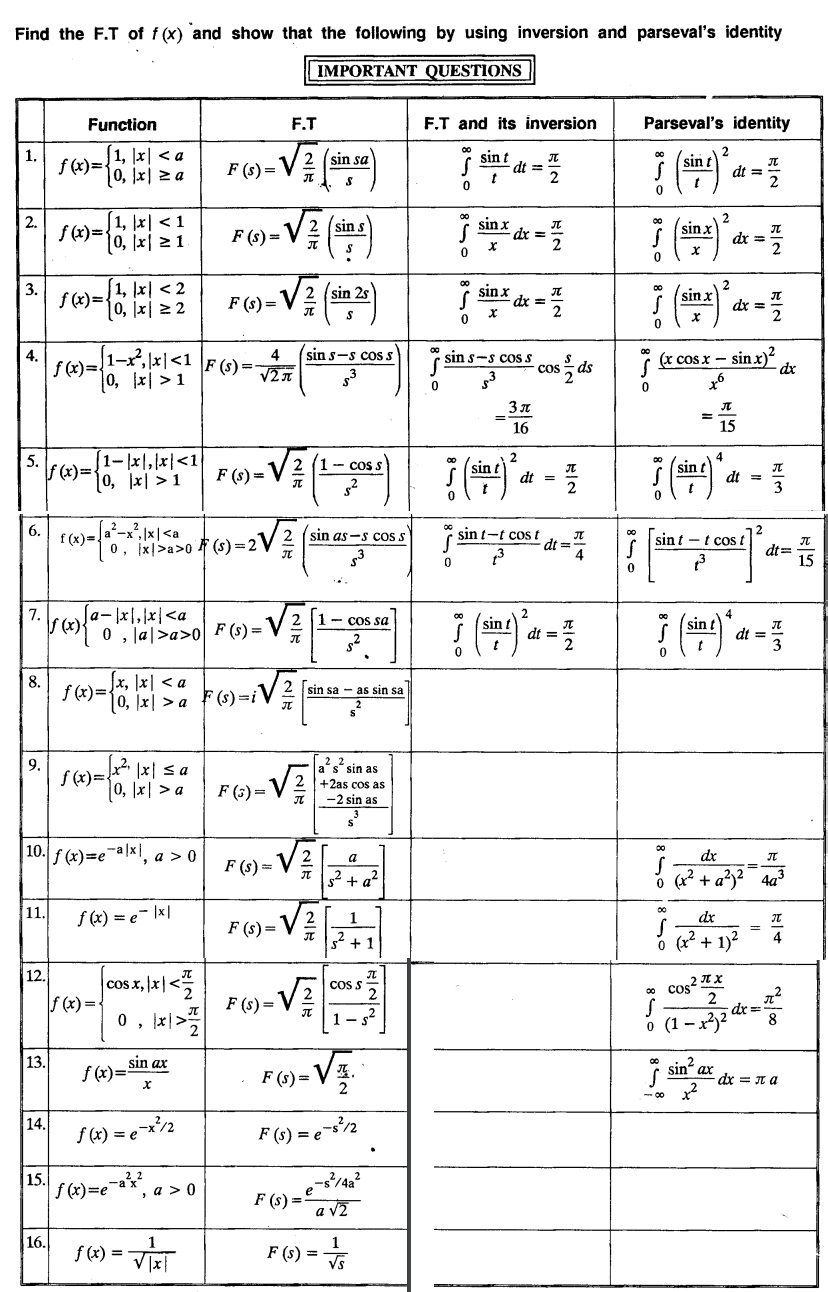
Transforms and Partial Differential Equations: Unit IV: Fourier Transforms
Fourier sine & Cosine transforms
Definition, Statement, Proof, Solved Example Problems
a. FOURIER COSINE TRANSFORM: The infinite Fourier cosine transform of f (x) is defined by
FOURIER SINE & COSINE TRANSFORMS : The infinite Fourier cosine transform of f (x) is defined by The inverse Fourier cosine transform Fc [f(x)] is defined by Let Fc(s) denote the F.C.T of f(x). Then Proof : By the definition of F.C.T, Here, f(x) is defined for all x ≥ 0 Clearly, g(-x) = g(x) for all x and hence g is an even function. To prove that, the Fourier transform of g(x) is the F.C.T of f(x). Hence, by inversion formula for F.T, we have The infinite Fourier sine transform of f(x) is defined by The inverse Fourier sine transform of Fs [f(x)] is defined by Let Fs(s) denote the F.S.T of f(x). Then Proof : By the definition of F.S.T Here, f(x) is defined for all x ≥ 0 Now, we define g(x) by Clearly, g(x) is an odd function F(g(x)] = Fs [f(x)] [by the above 5.8] 1. Linear property Proof: (i) We know that, (ii) We know that, 2. Modulation property: Proof : 4. Fs [f'(x)] = -s F'c (s), if f (x) → 0 as x→ ∞. [Transform of derivative] Proof : 5. [Transform of derivative] Proof : 6. [Derivatives of transform] Proof: We know that, Differentiating both sides w.r.to 's', we get 7. Proof: We know that, Differentiating both sides w.r.to 's', we get Ill(a). Problems based on Fourier Cosine Transform Example 4.3.a(1) : Find the Fourier cosine transform of Solution : Example 4.3.a(2) : Find the Fourier cosine transform of Solution: We know that, By integrating, we get Example 4.3.a(3): Find the Fourier cosine transform of e-ax, a > 0. Solution : Example 4.3.a(4) : Find the Fourier cosine transform of the function 3e-5x + 5e-2x. Solution : Example 4.3.a(5): Find the Fourier cosine transform of Solution: We know that, Example 4.3.a(6): Find the Fourier cosine transform of f(x) = x. Solution : We know that, Example 4.3.a(7): Find the Fourier cosine transform of e-ax cos ax. Solution: We know that, Example 4.3.a(8): Show that Solution : We know that, Hence, Example 4.3.a(9): Find the Fourier cosine transform of e-ax sin ax. Solution: We know that, Example 4.3.a(10): Evaluate Fc [xn-1] if 0 < x < 1. Deduce that Solution : Equating real parts, we get Using this in (1) we get Example 4.3.a(11): Find the Fourier cosine transform of Solution: We know that, Example 4.3.a(12): Find the Fourier cosine transform of Solution : We know that, Example 4.3.a(13): Find the Fourier cosine transform of Solution: We know that, Ill. (b) Problems based on Fourier cosine transform and its inversion formula. Example 4.3.b(1): Solve the integral equation Solution: Example 4.3.b(2): Solve the integral equation Solution : We know that, Fourier cosine inversion formula is We know that, From (1) and (2), we have Example 4.3.b(3): Find the Fourier cosine transform of e-|x| and deduce that Solution: Now, using Fourier cosine inversion formula Example 4.3.b(4): Find the Fourier cosine transform of e-ax, a > 0 and deduce that Solution: Applying the inversion formula, we have III. (c) Problems Based on Fourier Sine Transform. [F.S.T] Example 4.3.c(1): Find the Fourier sine transform of f(x) = e-x cos x. Solution: We know that, Example 4.3.c(2): Find the Fourier sine transform of Solution: We know that, Example 4.3.c(3): Find the Fourier sine transform of Solution: We know that, Example 4.3.c(4): Find the Fourier sine transform of 1/x. Solution: We know that, Example 4.3.c(5): Find the Fourier sine transform of 3e-5x + 5e-2x Solution: Example 4.3.c(6): Find the Fourier sine transforms of f(x) = e-ax Solution: Example 4.3.c(7): Find the Fourier sine transform of the function Solution: We know that, Diff. w.r.to s on both sides, Example 4.3.c(8): Find the Fourier sine transform of xn-1. Deduce that Solution: Example 4.3.c(9): Find the Fourier sine transform of Solution: III. (d) Problems based on Fourier sine transform and its inversion formula. Example 4.3.d(1): Find Fourier sine transform of e-ax, a > 0 and deduce that Solution: Applying the inversion formula, we get Example 4.3.d(2): Find the Fourier sine transform of e-x, Hence show that Solution: Changing 'x' to 'm' and 's' to 'x', we get Example 44d(3): Find f(x) if its sine transform is Hence, find Solution: Integrating w.r.to x, we get Example 4.3.d(4): Solve the integral equation Solution: By inversion formula, we get III.(e) Problems based on properties of F.C.T AND F.S.T. Example 4.3.e(1): (i) Find the Fourier cosine transform of (ii) Find the Fourier sine transform of Solution: Solving (6) & (7), we get Example 4.3.e(2): Find the Fourier sine and cosine transformations of xe-ax. Solution: Example 4.3.e(3): Find Fourier cosine transform of Solution : See Example 4.3 a(13), Page No. 4.97 Example 4.3.e(4): Find the Fourier sine transform of e-ax and hence find the Fourier cosine transform of xe-ax. Solution: We know that, III (f) Problems based on Parseval's identity in F.S.T and F.C.T Example 4.3.f(1): Evaluate : Solution : Parseval's identity is Note : (1) Evaluate: Solution : Step 1: (2) Evaluate : Solution : Example 4.3.f(2): Using Fourier sine transform, prove that Solution : Parseval's identity is Solution: Example 4.3.f(3) : Using transform methods, evaluate Solution : Parseval's identity is Example 4.3.f(4): Using transform methods, evaluate Solution : Parseval's identity is Example 4.3.f(5): Using Parseval's identity of the Fourier cosine transform, Evaluate Solution : Parseval's identity is 1. Find the Fourier transform of the function. I. 1. Find the Fourier cosine transform of e-4x. Deduce that II. Find the Fourier Cosine Transform of III. Find the Fourier Sine transform of IV. Find the Fourier cosine and sine transforms ofa. FOURIER COSINE TRANSFORM:
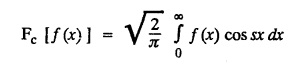
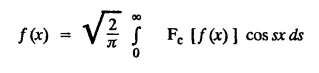
b. INVERSION FORMULA FOR FOURIER COSINE TRANSFORM
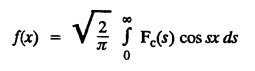
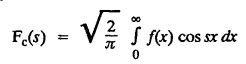
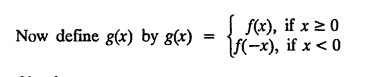
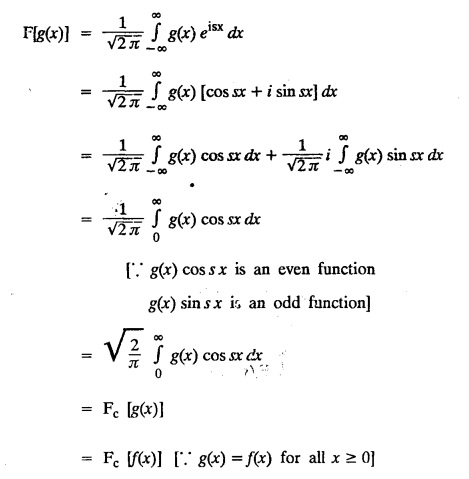
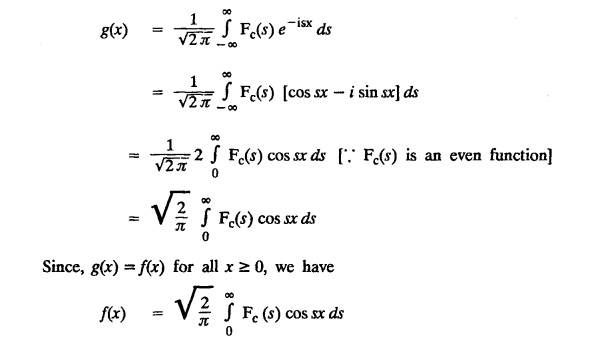
c. FOURIER SINE TRANSFORM:
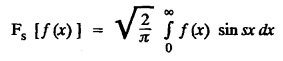
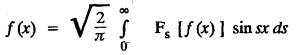
d. INVERSION FORMULA FOR FOURIER SINE TRANSFORM
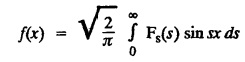
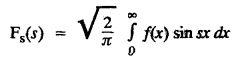
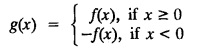
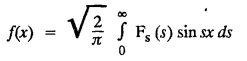
e. Properties of Fourier sine transform and Fourier cosine transform
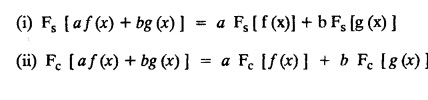
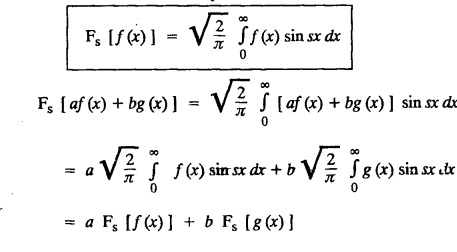
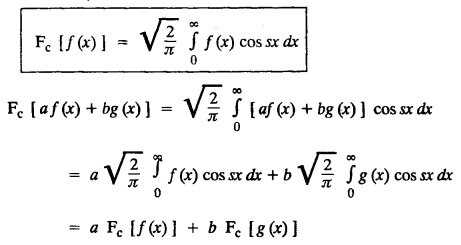
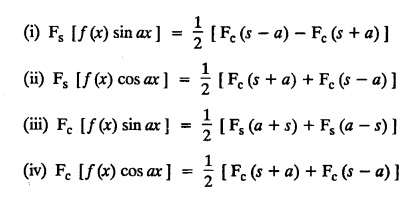

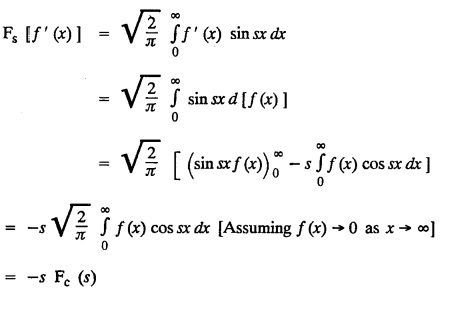
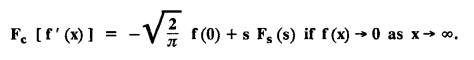
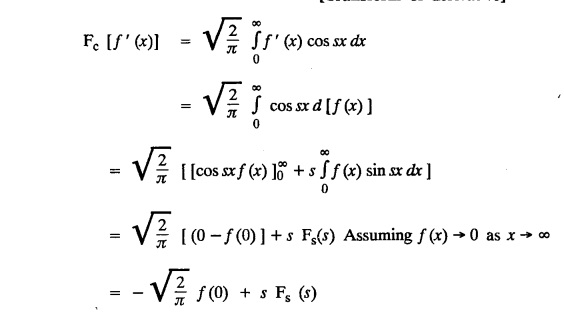
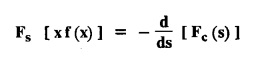
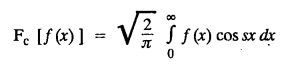
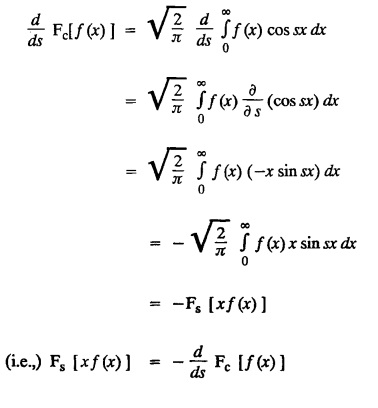
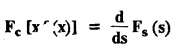
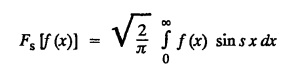
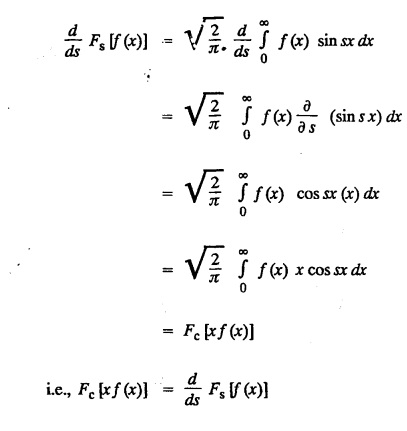
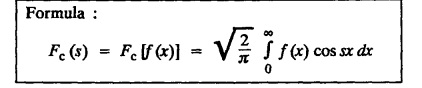
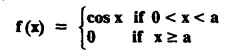

![]() and hence, find
and hence, find 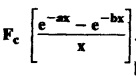


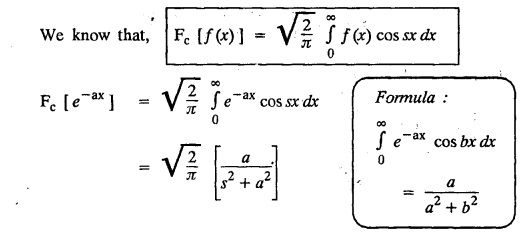
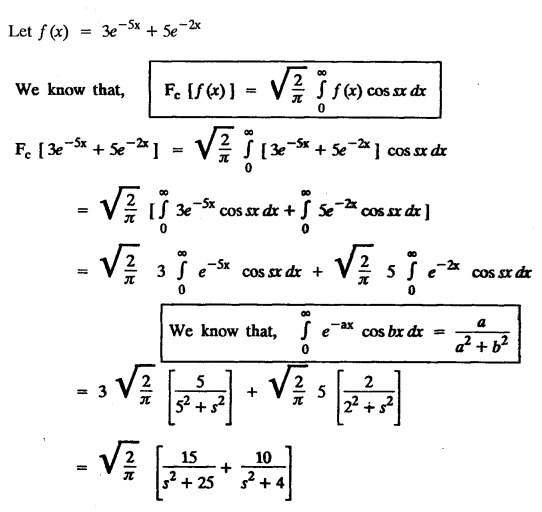
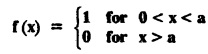
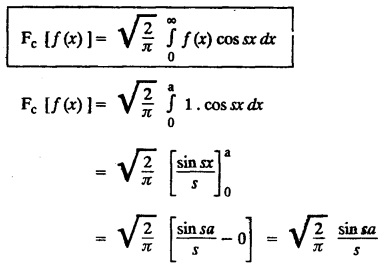
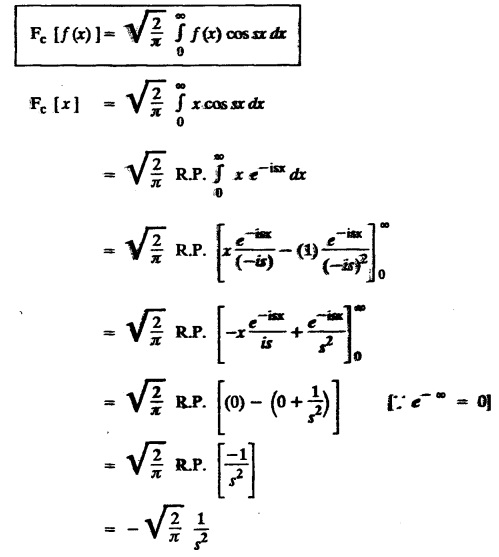

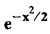 is self-reciprocal under Fourier cosine transform.
is self-reciprocal under Fourier cosine transform.
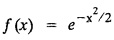 is self reciprocal with respect to Fourier cosine transform.
is self reciprocal with respect to Fourier cosine transform.
![]() is self reciprocal under Fourier cosine transform.
is self reciprocal under Fourier cosine transform.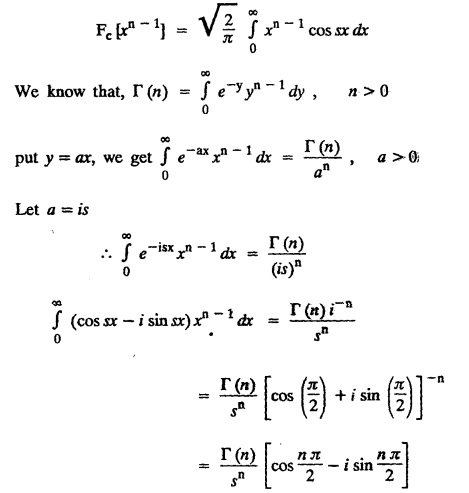
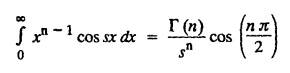

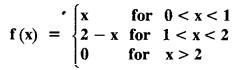

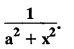
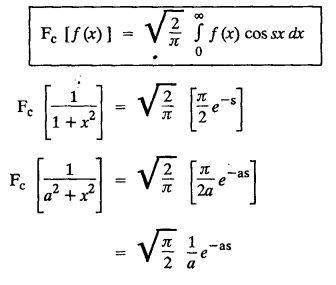
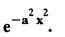

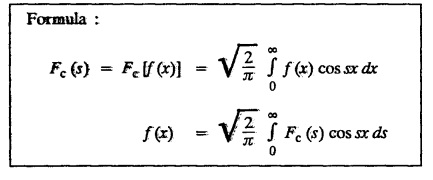
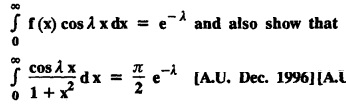

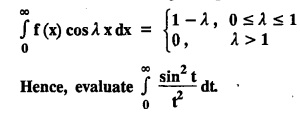
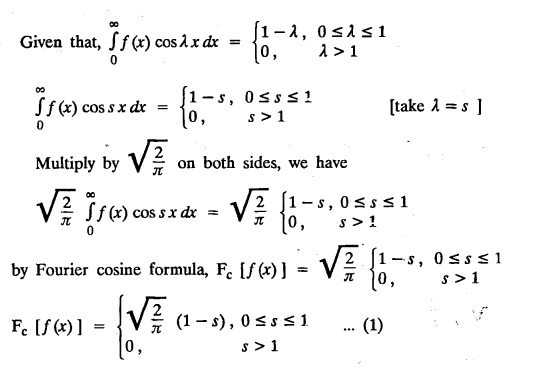
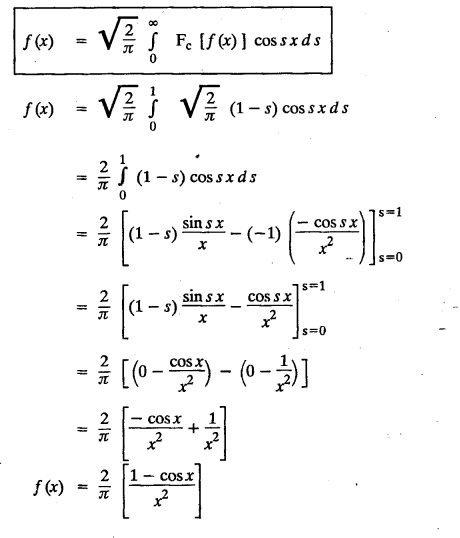
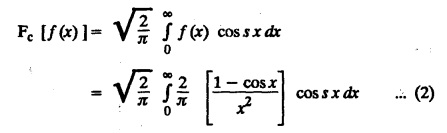

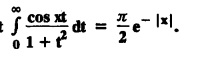
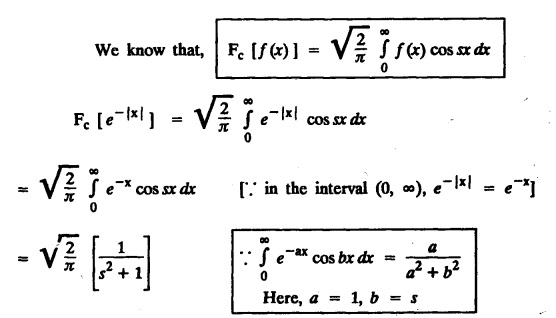
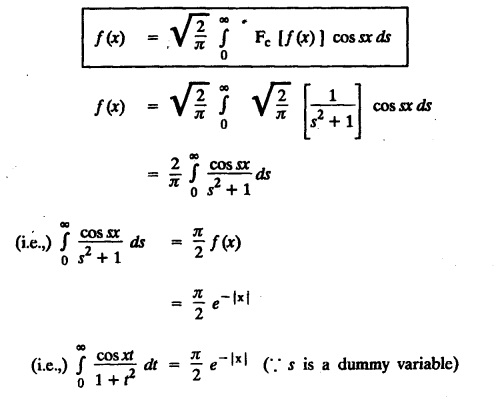
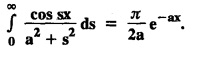
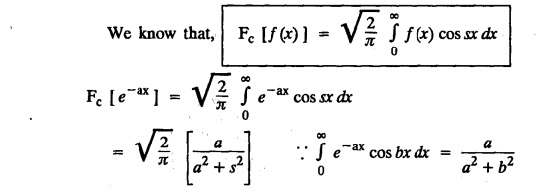
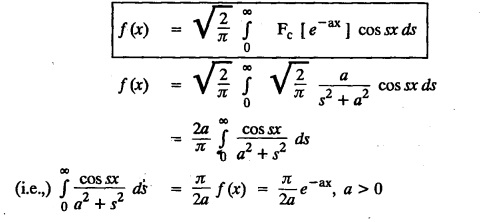
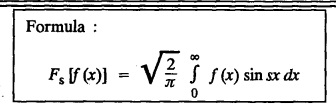
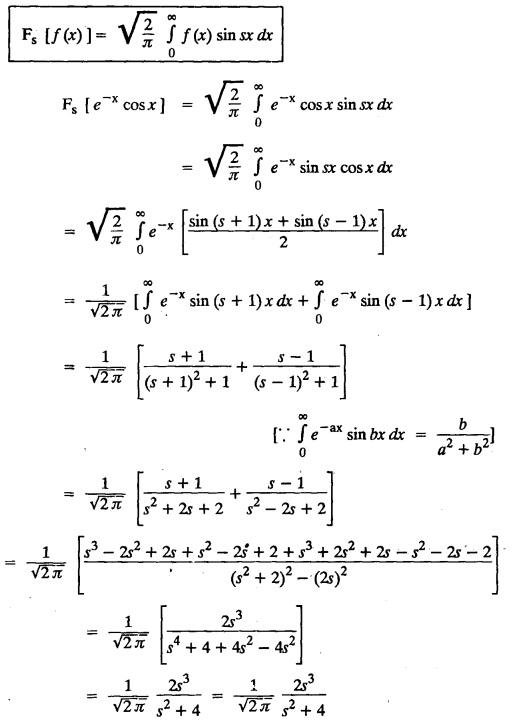
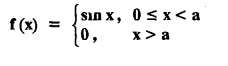
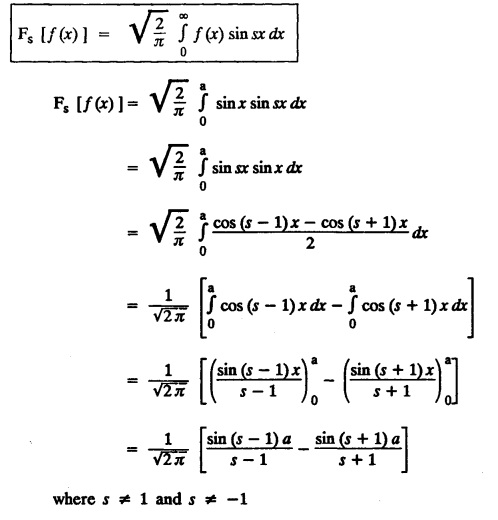
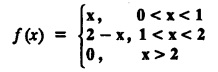



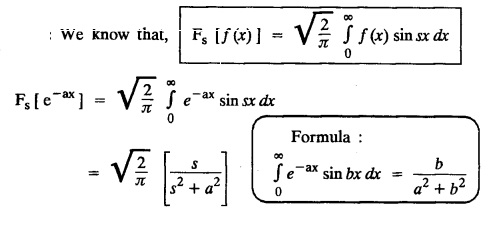
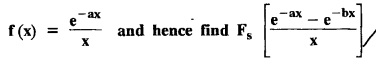
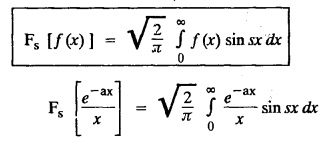

![]() is self reciprocal under Fourier sine transform.
is self reciprocal under Fourier sine transform.
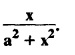
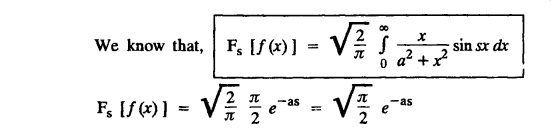
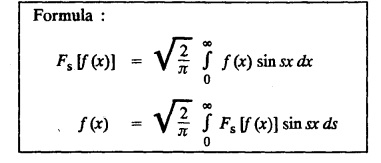
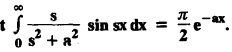
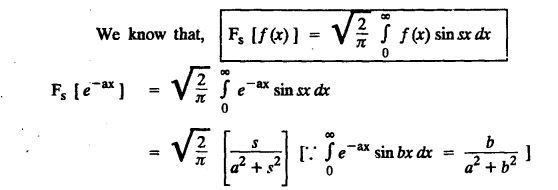
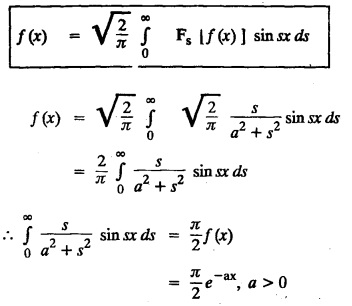
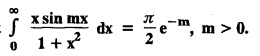

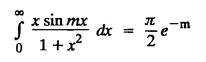
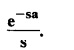
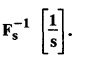

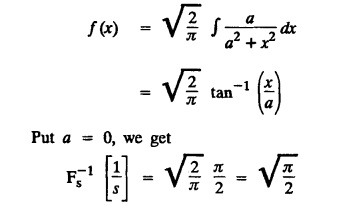
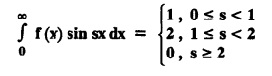
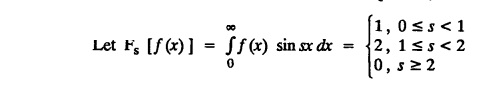
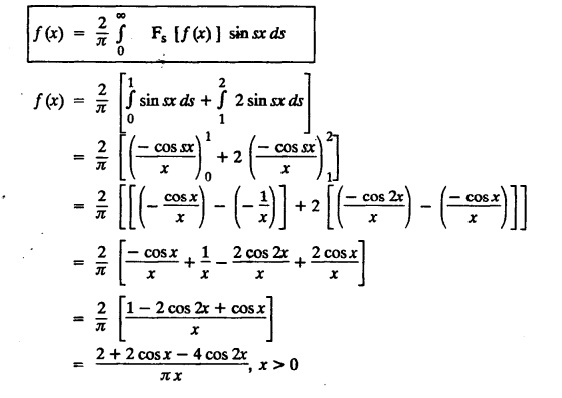
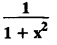
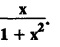



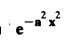 and hence find
and hence find 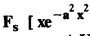 ]
]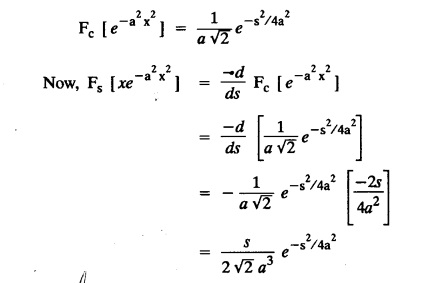
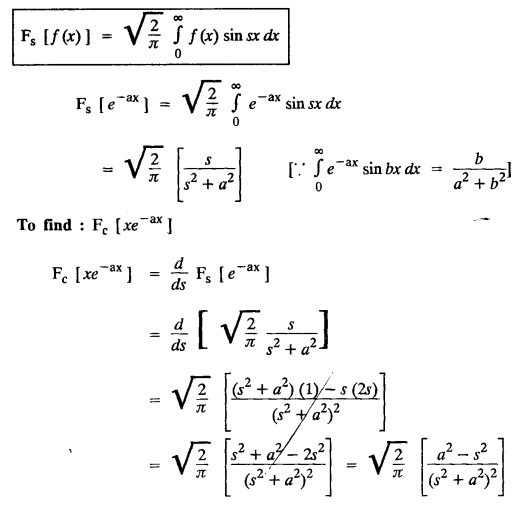
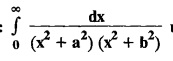 using transforms.
using transforms.
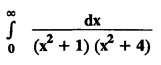
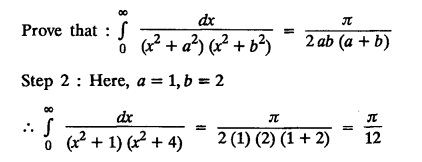
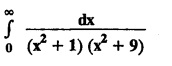
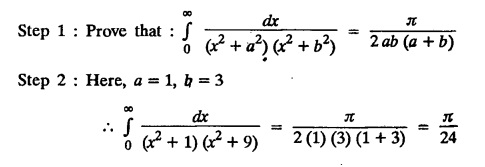
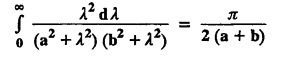

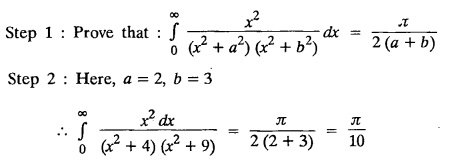
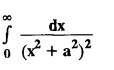

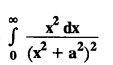 where a > 0.
where a > 0. 
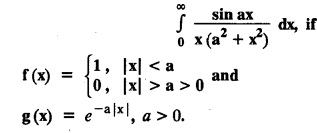

EXERCISE 4.1 [Fourier integral theorem

EXERCISE 4.2 [Fourier Transform]

EXERCISE 4.3 [FCT and FST]
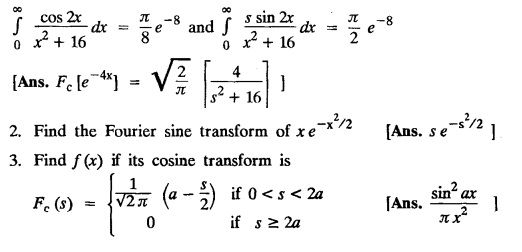
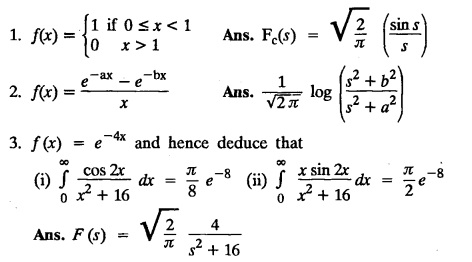
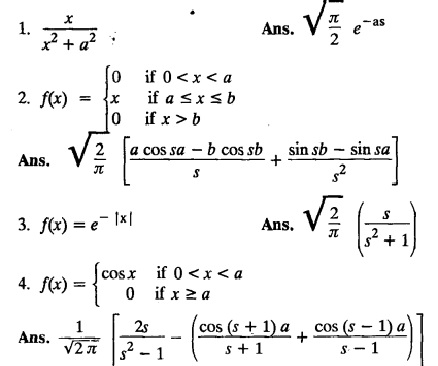
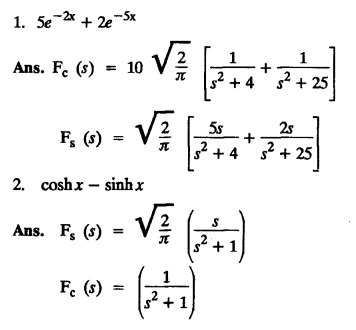
Transforms and Partial Differential Equations: Unit IV: Fourier Transforms : Tag: : Definition, Statement, Proof, Solved Example Problems - Fourier sine & Cosine transforms
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
