Transforms and Partial Differential Equations: Unit II: Fourier Series
Fourier Series
Uses, Definition of Periodic Function, Continuity of a Function, Examples, Advantages, Solved Example Problems
Fourier series, is named after the French Mathematician cum physicist Jean-Baptiste Joseph Fourier (1768 - 1830).
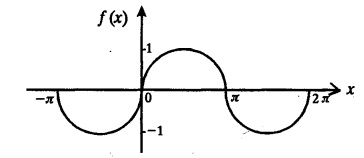
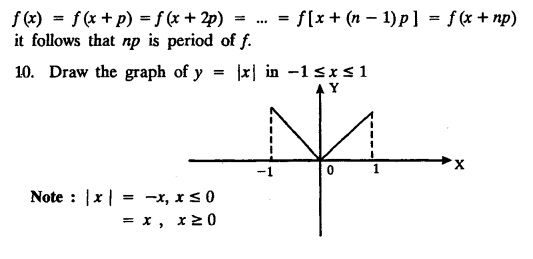
UNIT - II FOURIER SERIES Drichlet’s conditions - General Fourier series - Odd and even functions - Half range sine series - Half range cosine series Complex form of Fourier Series Parseval's identity - Harmonic Analysis. Fourier series, is named after the French Mathematician cum physicist Jean-Baptiste Joseph Fourier (1768 - 1830). He introduced Fourier Series in 1822, while he was investigating the problem of heat conduction. The series of sines and cosines are known after him. Fourier Series are series of cosine and sine terms and arise in the important practical task of representing general periodic functions. They constitute a very important tool in solving problems that involve ordinary and partial differential equations. § Use of Fourier Series: Fourier series are particularly suitable for expansion of periodic functions. We come across many periodic functions in voltage, current, flux, density, applied force, potential and electromagnetic force in electricity. Hence, Fourier Series are very useful in electrical engineering problems. Definition : Periodic Function A function f(x) is said to be periodic, if and only if ƒ (x + p) = f (x) is true for some value of p and every value of x. The smallest value of p for which this equation is true for every value of x will be called the period of the function f(x). Example : 1. sinx = sin (x + 2π) = sin (x + 4π) = …. So sinx is a periodic function with the period 2π. This is also called Sinusoidal periodic function. 2. The trignometric functions sinx and cosx are periodic functions with functions fundamental (primitive) period 2π. 3. sin 2x and cos 2x are also periodic functions with fundamental period π. 4. tanx is a periodic function with period π. 5. Find the period of sin nx where n is a positive integer Solution: 6. Show that a constant has any positive number as period. Solution : Let f(x) = c, where c is a constant. then f(x + k) = c, k being any positive number that is f(x+k) = f(x) So f(x) is periodic with period k. Note : Since, there is no least value of k, we say that ƒ (x) = c has no fundamental period. 7. Let f : R →R be the function defined by Let p be any rational number. If x is rational, then x+p is also rational and if x is irrational, then x+p is also irrational. Hence, every rational number is a period of ƒ and ƒ has no fundamental period. 8. Let ƒ and g be periodic functions with period p and let a and b be real numbers. Prove that af + bg is also a periodic function with period p. Solution: Since, ƒ and g are periodic with period p Hence, af + bg is periodic with period p. 9. If p is a period of f(x), show that np is also a period where n is any integer (positive or negative) Solution: Since The left hand limit of ƒ (x) at x = a is defined as x approaches a from the left and is denoted by ƒ (a −). The right hand limit of ƒ (x) at x = a is defined as x approaches a from the right and is denoted by ƒ (a +) A function f(x) is said to be continuous at x = a if ƒ (a +) = ƒ (a) = ƒ (a −) Note: 1. f(a) is different from ƒ (a +) and ƒ (a −), ƒ (a) means the value of ƒ (x) at x = a. 2. If there is a finite jump in the graph of y f(x) at x = a, the function is not continuous at x = a. (i.e.,) The function is not defined at x = a. In such cases, both right hand and left hand limits are not equal. The function f(x) is piecewise continuous in an interval (a, b) means that f(x) is continuous at all, but a finite number of points in (a, b). 1. Discontinuous function can be represented by Fourier series, although derivatives of the discontinuous functions do not exist. (This is not true for Taylor's series). 2. The Fourier series is useful in expanding the periodic functions, since outside the closed interval, there exists a periodic extension of the function. 3. Expansion of an oscillating function by Fourier series gives all modes of oscillation (fundamental and all overtones) which is extremely useful in physics. 4. Fourier series of a discontinuous function is not uniformly convergent at all points. 5. Term by term integration of a convergent Fourier series is always valid, and it may not be valid if the series is not convergent. However, term by term, differentiation of a Fourier series is not valid if the series is not convergent.INTRODUCTION
§ PERIODIC FUNCTION :
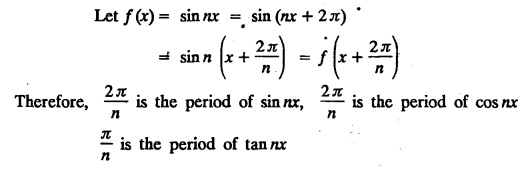
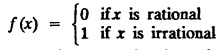
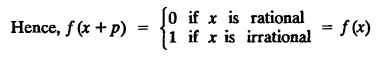
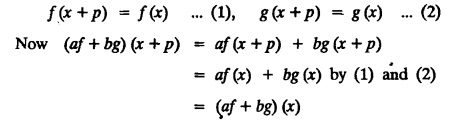
§ CONTINUITY OF A FUNCTION :
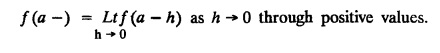
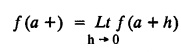
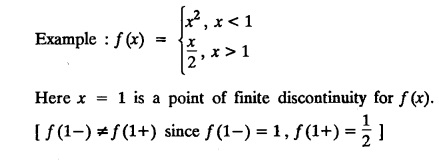
§ ADVANTAGES OF FOURIER SERIES :
Transforms and Partial Differential Equations: Unit II: Fourier Series : Tag: : Uses, Definition of Periodic Function, Continuity of a Function, Examples, Advantages, Solved Example Problems - Fourier Series
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
