Transforms and Partial Differential Equations: Unit II: Fourier Series
Fourier Series: Definition, Euler's Formula, Convergence Theorem, Important Formulae
with Solved Example Problems
Periodic functions occur frequently in engineering problems. Such periodic functions are often complicated.
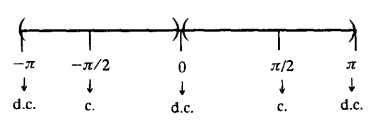
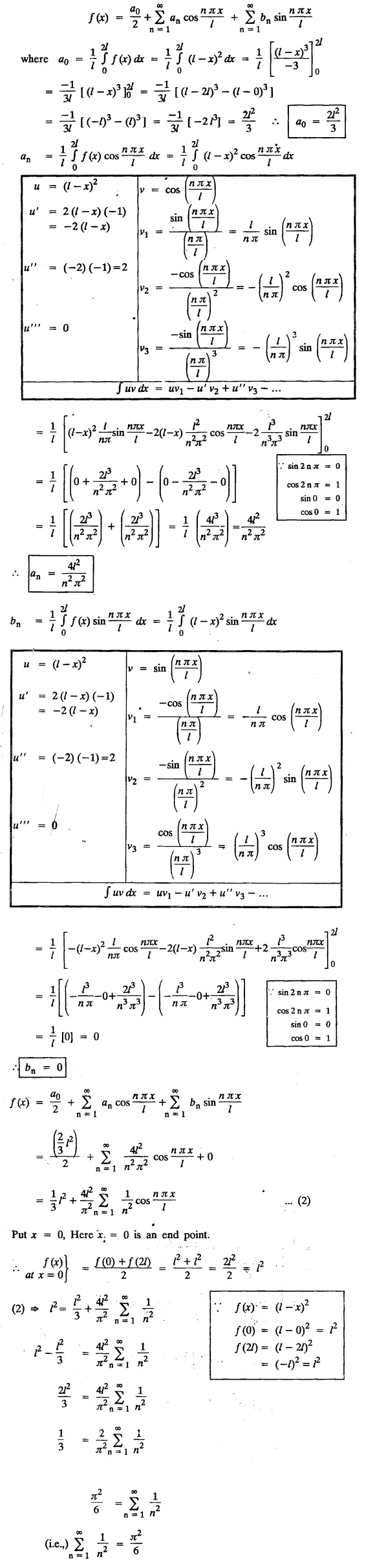
FOURIER SERIES Periodic functions occur frequently in engineering problems. Such periodic functions are often complicated. It is therefore desirable to represent these in terms of the simple periodic functions of sine and cosine. Here, we express a non-sinusoidal periodic function into a fundamental and its harmonics, a series of sines and cosines of an angle and its multiples of the form. If a function f(x) defined in c < x < c + 2π can be expanded as the infinite trigonometric series, Formula (1), (2) and (3) are known as the Euler formulas. Note: Only if the constant term is taken as a0/2, formula (2) is true for n = 0. To establish Euler formulae, the following integrals will be required." Let f (x) be represented in the interval (c, c + 2л) by the Fourier Series We assume that the series (1) can be integrated term by term x = c to x = c + 2π To find a0 : Integrate both sides of equation (1) from To find an: Multiply both sides of (1) by cos nx and integrate from To find bn Multiply both sides of (1) by sin nx and integrate from In practice, we often require to find a Fourier series for an interval which is not of length 2л. In many problems, the period of the function to be expanded is not 2л, but some other interval say 2l. Suppose f(x) is defined in the interval (−1, 1). Example 2.1.1. State the Euler's formulae when f(x) is expanded as a Fourier series in c < x < c + 2 л. Solution: The Fourier Series for f(x) in the c < x < c + 2 л Formulas (1), (2) and (3) are known as the Euler formulas. Example 2.1.2. Write the formula for finding Euler's constant of a Fourier series in (0, 2π). Solution: Let the Fourier Series for f(x) in (0), 2π) be Formulas (1), (2) and (3) are known as the Euler formulas. Example 2.1.3. Write the formula for finding Euler's constant of a Fourier series in (-π, π ). Solution: Let the Fourier Serics for f(x) in (− π, π) bе Formulas (1), (2) and (3) are known as the Euler formulas. Example 2.1.4. Write the formula for Fourier Constants for f(x) in (c, c + 2l). Solution: The Fourier expansion for f(x) in the interval c < x < c + 2l is given by Example 2.1.5. Write the formula for Fourier Constants for f(x) in (0, 2l). Solution : The Fourier expansion for f (x) in the interval 0 < x < 2l is given by Example 2.1.6. Write the formulas for Fourier Constants for f(x) in (-l, l). Solution: The Fourier expansion for f(x) in the interval –l < x < l is given by Any function f(x) can be developed as be developed as a Fourier series (i) f(x) is periodic, single-valued and finite (ii) ƒ(x) has a finite number of finite discontinuities in any one period and has no infinite discontinuity. (iii) f(x) has at the most a finite number of maxima and minima. Note 1: Dirichlet's conditions are not necessary but only sufficient for the existence of Fourier series. Note 2 : Peter Gustav Lejenune Dirichlet (1805 - 1859), Great German Mathematician is known for his contributions to Fourier Series and Number Theory. Note 3 : tan x cannot be expanded as a Fourier series, since tanx has infinite number of infinite discontinuties, so Dirichlet's conditions are not satisfied. Note 4 : cosec x cannot be expanded as a Fourier series, since one of the Dirichlet's conditions is not satisfied. Example 2.1.7 The function Solution : At x = 2, f(x) becomes infinity, it has an infinite discontinuity at x = 2 So it does not satisfy one of the Dirichlet's conditions. Hence it cannot be expanded as a Fourier series. Example 2.1.8: Can you expand Solution : This function is well defined in any finite interval in the range (-∞, ∞) it has no discontinuities in the interval Differentiate f(x) is maximum or minimum when f'(x) = 0 (ie.,) when 4x = 0, (i.e.,) x = 0 So it has only one extreme value, and has (i.e.,) a finite number of maxima and minima in the interval (-∞, ∞) Since it satisfies all the Dirichlet's conditions, it can be expanded in a Fourier Series in a specified interval in the range (∞, ∞∞). Example 2.1.9: Examine whether the function sin 1/x can be expanded in a Fourier series in π ≤ x ≤ π Solution : where n is zero or an integer. For large values of n as n → ∞, the values of x as given by (2) tend to become indefinitely small and to be crowded near to the value of x = 0. Hence, the function (1) has an infinite number of maxima and minima near x = 0, so it does not satisfy one of the Dirichlet's conditions. It cannot be expanded in a Fourier series in the range –л ≤ x ≤ л in which the point x = 0 is included. Statement: If f(x) is a periodic function with period 2л and f(x) and f'(x) are piecewise continuous on [-л, л], then the Fourier series is convergent. The sum of the Fourier series is equal to f (x) at all points of x where f(x) is continuous. At the points of where f(x) is discontinuous, the sum of the Fourier series is the average of the right and left limits, that is 1/2 [f(x+) +ƒ (x−)] Note : • In the interval (0, 2л) i.e., 0 < x < 2 л x continuous at all points except 0 and 2л • In the interval [0, 2π] i.e., 0 ≤ x ≤ 2π x continuous at all points including 0 and 2л • In the interval (-л, л) i.e., -π < x < π x continuous at all points except at -л and л • In the interval [-л, л] i.е., -л ≤ x ≤ л x continuous at all points including -л and л • In the interval (-л, 0) and (0, л) i.е., -л < x < 0 and 0 < x < л x continuous at all points excерt -л, л and 0. Note: If f(x) is defined in the interval (0, 2л), then Example 2.1.10 Sum the Fourier series for f (x) = 1/2 (π − x) Solution : Example 2.1.11: Sum the Fourier series for Solution: Example 2.1.12 Sum the Fourier series for Solution : x = 1 is a finite point of discontinuity (in the middle) of (0, 2) Example 2.1.13: Sum the Fourier series for Solution : Note : 2.1.(a) PROBLEMS UNDER THE INTERVAL (0, 2π) Example 2.1.a(1) : If f (x) = 1/2 (π − x), find the Fourier series of period 2л in the interval (0,2 л). Hence deduce that Solution: Let the required Fourier series be Example 2.1.a(2): Expand f(x) = x(2л - x) as Fourier series in (0, 2л) and hence deduce that the sum of Solution : Example 2.1.a(3) : Determine the Fourier series for the function f(x) = x2 of period 2л in 0 < x < 2л. Solution : Let the required Fourier series be Example 2.1.a(4) : Expand f(x) = eax as a Fourier series in (0, 2л). Solution : Let the required Fourier series be Example 2.1.a(5) : Obtain the Fourier series of periodicity 2л for f(x) = e-x in the interval 0 < x < 2л. Hence deduce that the value of Solution: Let the required Fourier series be Example 2.1.a(6) Expand in Fourier series of f(x) = x sin x for 0 < x < 2л and deduce the result Solution: Let the required Fourier series be Example 2.1.a(7) : Obtain the Fourier series for the function Solution: Let the required Fourier series be Example 2.1.a(8): If Solution: Let the required Fourier series be Example 2.1.a(9): Find the Fourier series of periodicity 2л for Solution: Let the Fourier series be Problems under the interval (0, 2л) 1. Show that in the range 0 to 2л the Fourier series expansion for 2.1(b) PROBLEMS UNDER THE INTERVAL (0, 2l) Example 2.1.b(1) : Find the Fourier series expansion of period 2l for the function f(x) = (l-x)2 in the range (0, 2l). Deduce that Solution: Let the Fourier series be Example 2.1.b(2) Find the Fourier series expansion of f (x) = ex in (0, 2l) Solution: Let the Fourier series be Example 2.1.b(3) Find the Fourier series of Solution: Let the Fourier series be Example 2.1.b(4) : Find the Fourier expansion of Solution: Example 2.1.b(5) : Find the Fourier series of the function f(x)) = 2x − x2 for 0 < x < 3 and f (x + 3) = f(x). Solution: Example 2.1.b(6) If Solution: Here 2l = 2, l = 1 Let the required Fourier series be Example 2.1.b(7) Obtain Fourier series for f(x) of period 2l and defined as follows Solution: Let the required Fourier series be Exercise 2.1.(b) Problems under the interval (0, 2l) 1. Find the F.S. for the function 2. Find the F.S. io represent the following functions 3. Find the F.S. of period 21 for the function f(x) = x(2l – x) in (0, 2L). Deduce the sum of 4. Find the F.S of f (x) = x2 in (0, 2l). Hence deduce that 5. Find the F.S. expansion of ƒ (x) = x (1 − x) (2 −x) in (0, 2). 6. Find the F.S. expansion of ƒ (x) given by 7. Find the Fourier series for Definition : Fourier Series :
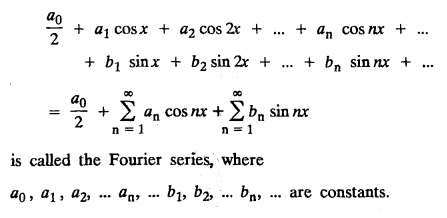
EULER'S FORMULA FOR THE FOURIER COEFFICIENTS

§ Useful Integrals to establish Euler formulae :
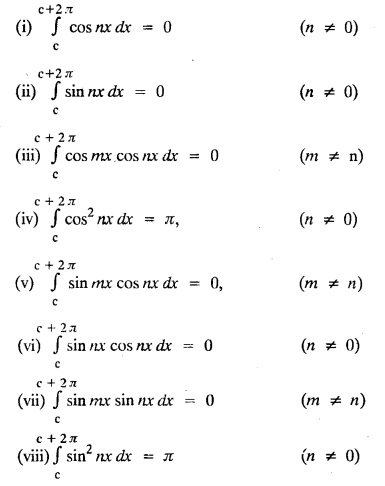
DETERMINATION OF FOURIER COEFFICIENTS : (Euler's Formulae)
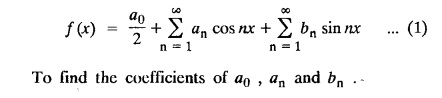
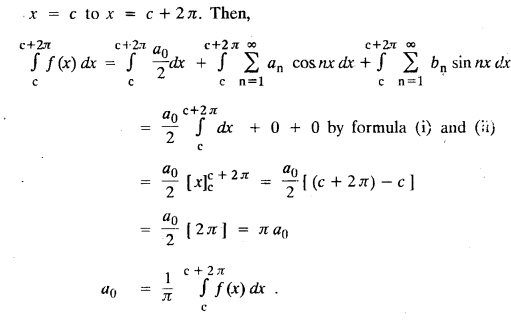

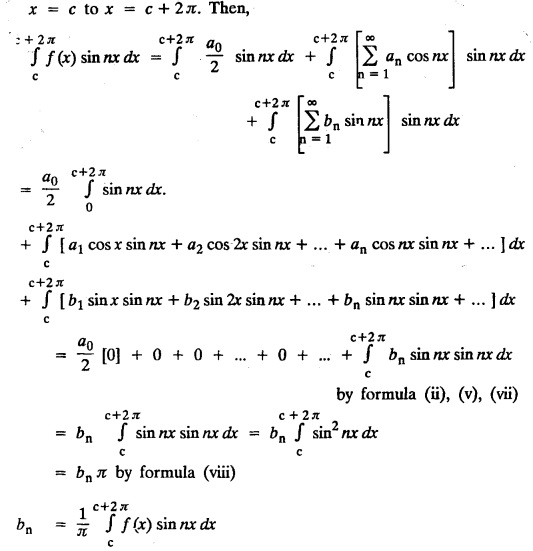
§ CHANGE OF INTERVAL

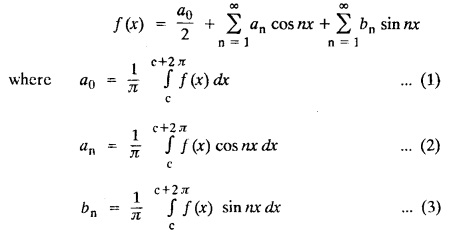
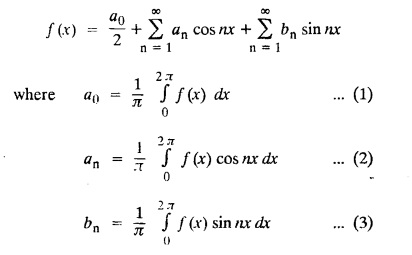
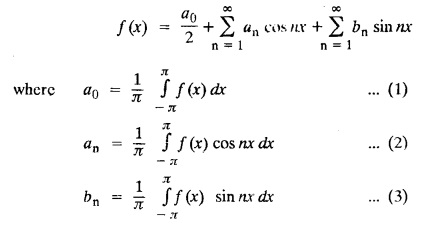

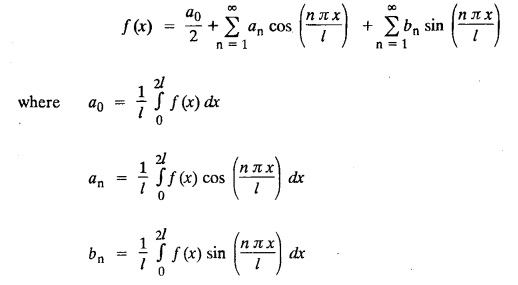
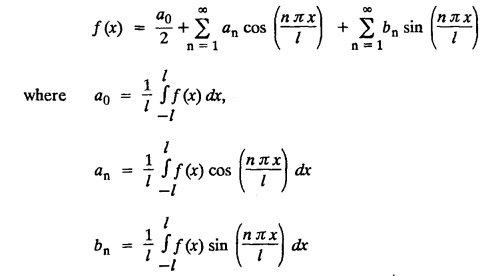
CONDITIONS FOR A FOURIER EXPANSION : [Dirichlet's Conditions]
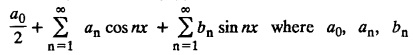 are constants, provided.
are constants, provided.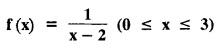 cannot be expanded as a Fourier series. Explain why ?
cannot be expanded as a Fourier series. Explain why ?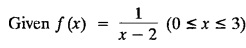
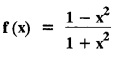 as a Fourier series in any interval.
as a Fourier series in any interval.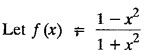
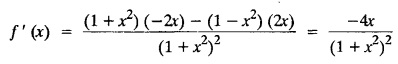

§ Convergence Theorem on Fourier Series :
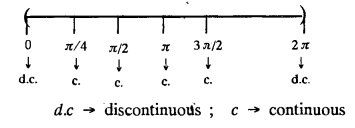
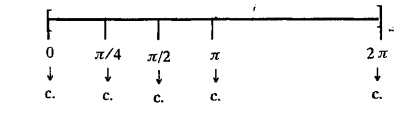
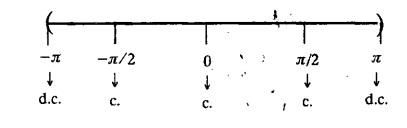
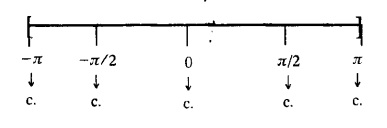
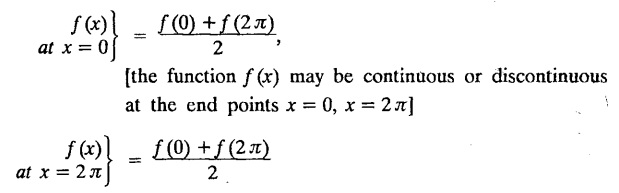

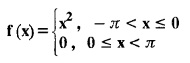

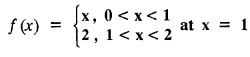
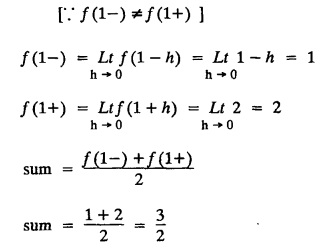
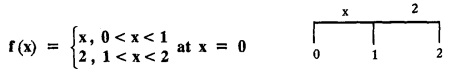
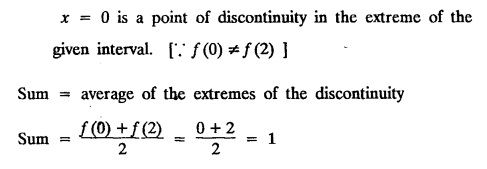
§ IMPORTANT FORMULAE
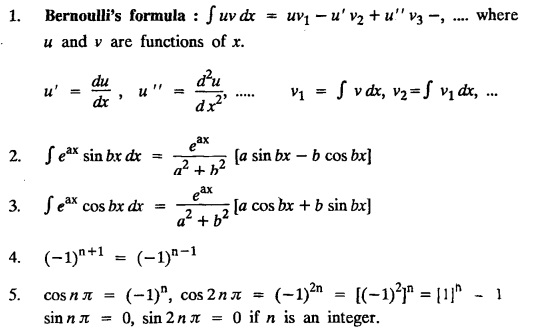
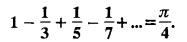

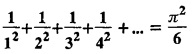



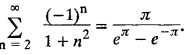 Further derive a series for cosech л.
Further derive a series for cosech л.
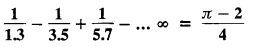

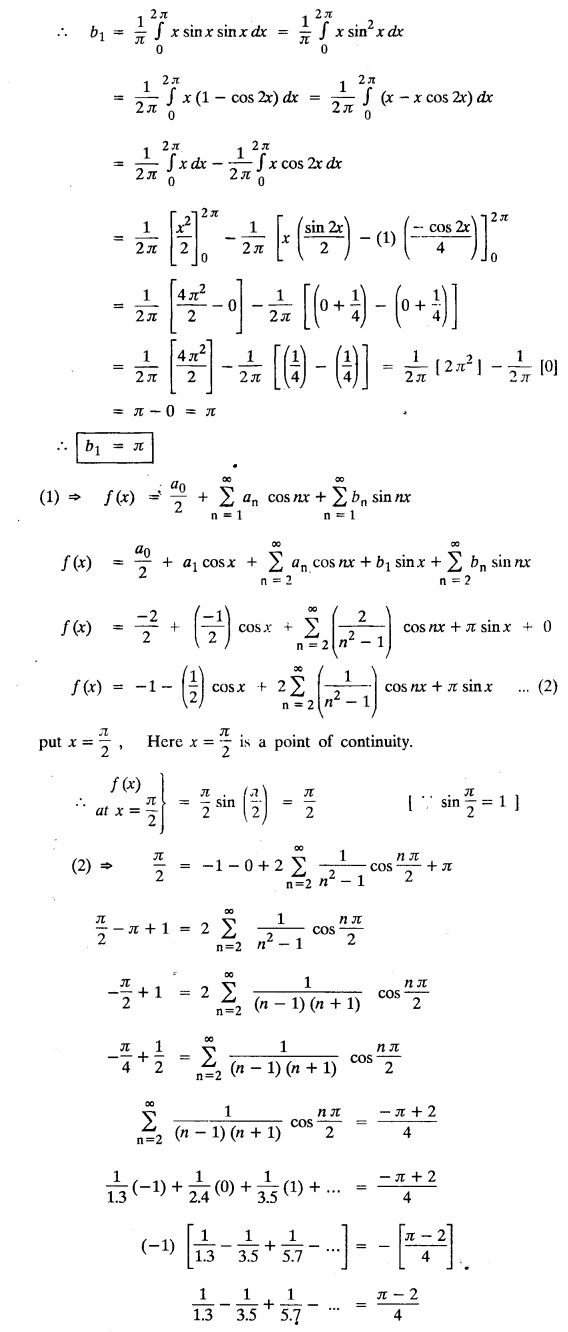
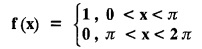



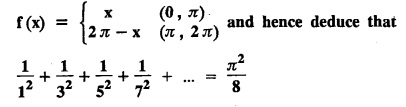
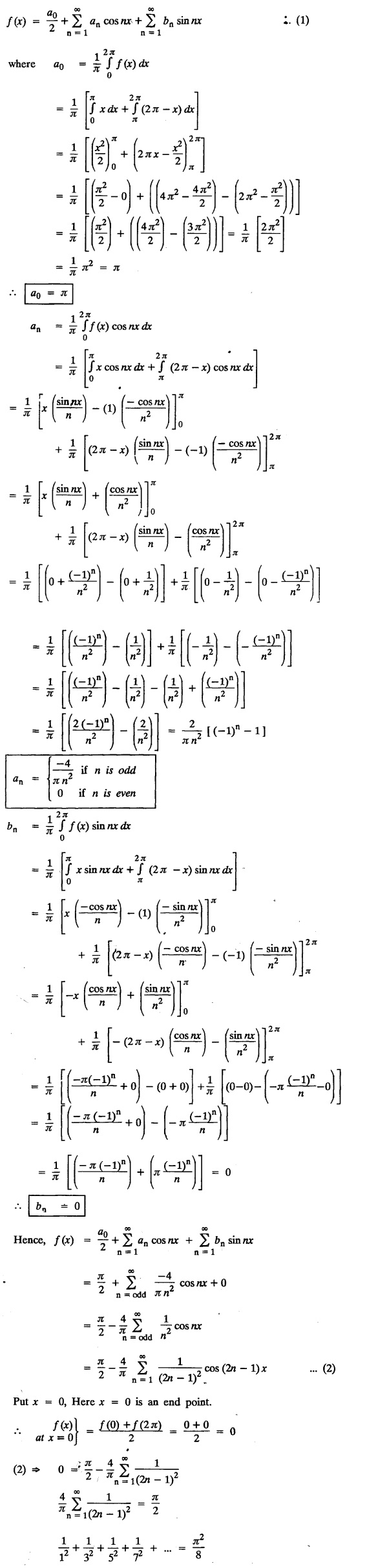
Exercise 2.1.(a)
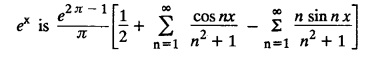

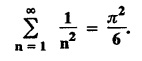
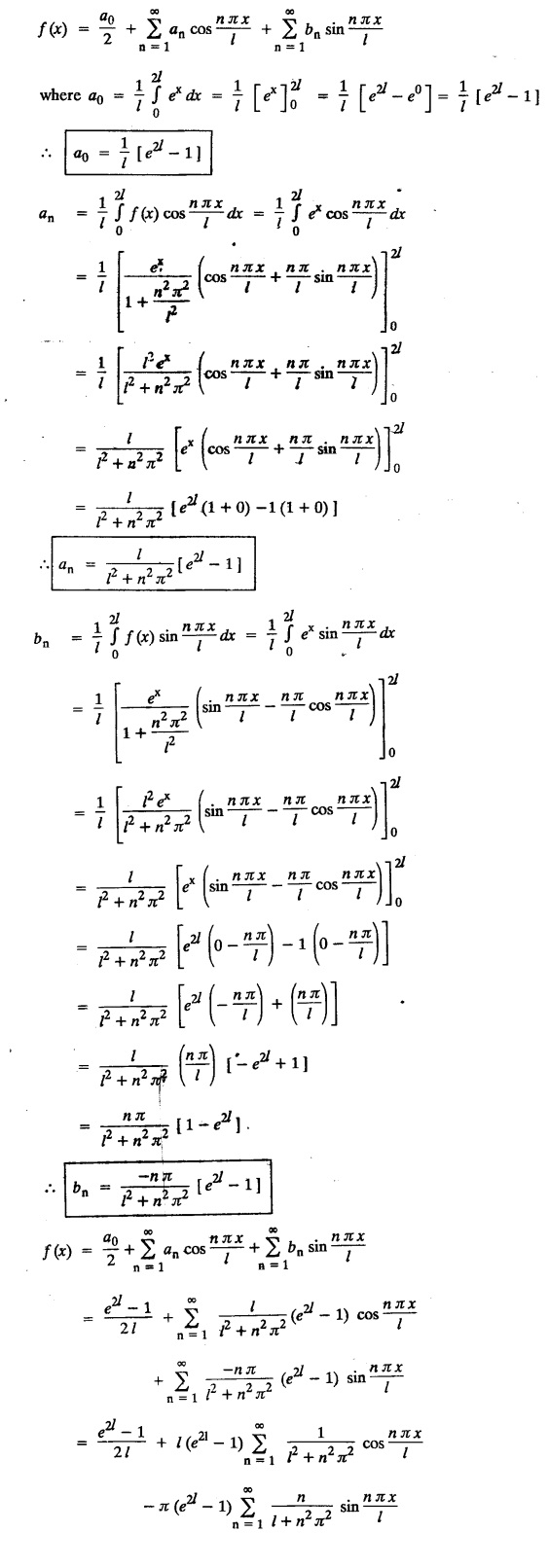
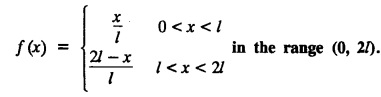

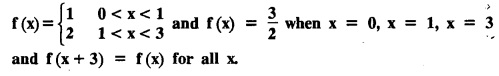
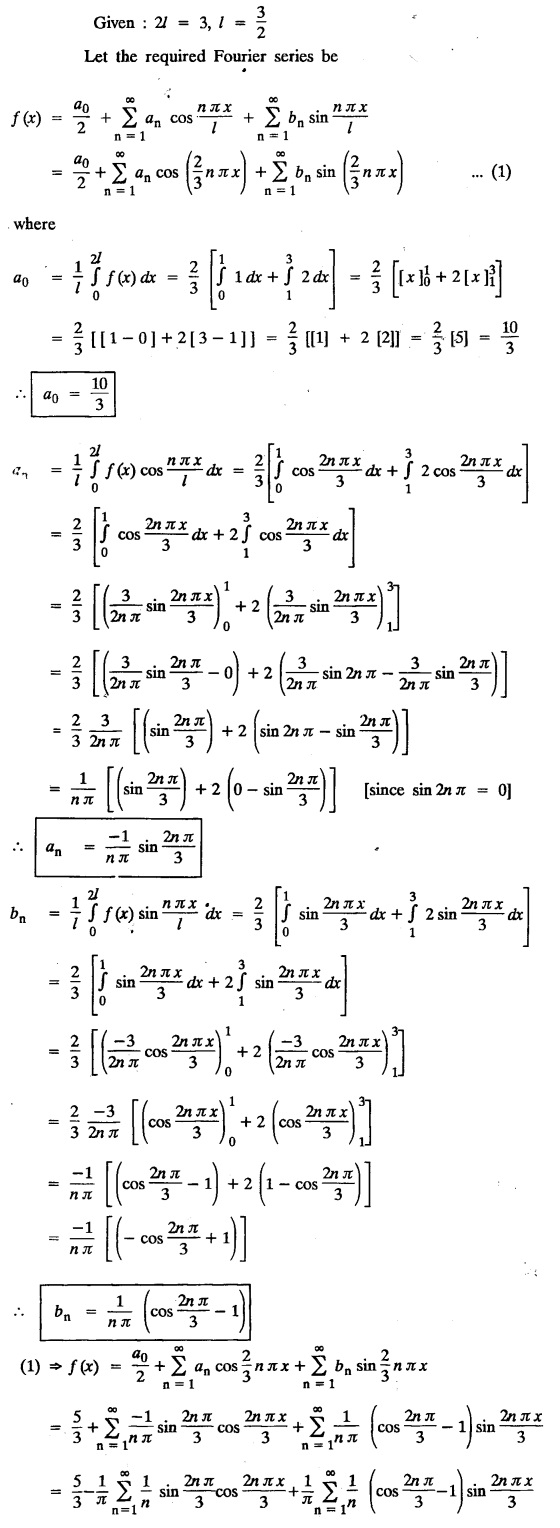

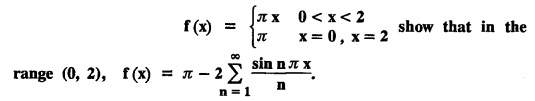

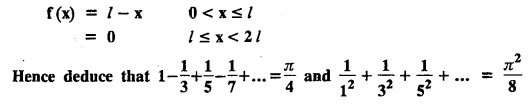

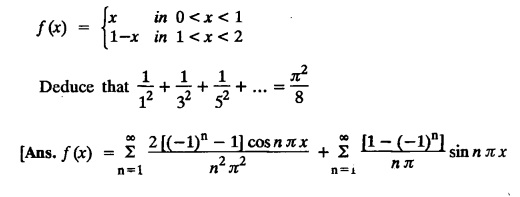
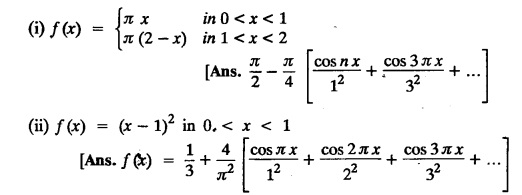
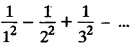
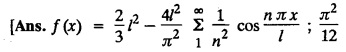

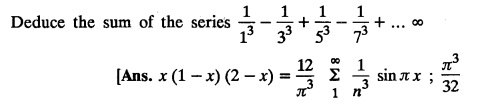
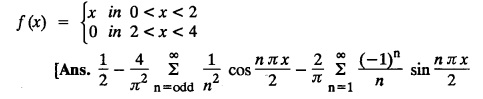
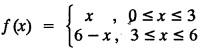
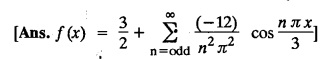
Transforms and Partial Differential Equations: Unit II: Fourier Series : Tag: : with Solved Example Problems - Fourier Series: Definition, Euler's Formula, Convergence Theorem, Important Formulae
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
