Theory of Machines: Unit II: Gears and Gear Trains
Formulae summary
Gears and Gear Trains - Theory of Machines
Before proceeding to numerical problems, the various formulae required are summarised in Table 4.4 below for easy reference.
FORMULAE SUMMARY • Before proceeding to numerical problems, the various formulae required are summarised in Table 4.4 below for easy reference. Table 4.4. Formulae summary Example 4.3 A pinion having 30 teeth drives a gear having 50 teeth. The profile of gears in involute with 20° pressure angle, 4 mm module and the standard addendum of 1 module. Find the length of path of contact, arc of contact and contact ratio. Given data: TP = 30; TG = 50; ϕ = 20°; m = 4 mm; Addendum, aP = aW = 1 module Solution: (i) Length of path of contact: Pitch circle radii of pinion and gear wheel are given by Addendum radii of pinion and gear wheel are given by (ii) Length of arc of contact: (iii) Contact ratio: Example 4.4 A pair of gears, having 40 and 20 teeth, respectively are of 20° involute form. The addendum length is 5 mm and module pitch is 5 mm. If the smaller wheel is driver and rotates at 2000 rpm. Find the velocity of sliding (i) at the point of engagement, (ii) at the point of disengagement, and (iii) at the pitch point. [A.U., May/June 2007] Given data: TG = 40; TP = 20; ϕ = 20°; Addendum, aP = aW = 5mm; m = 5 mm; NP = 2000 rpm. Solution: Pitch circle radii of pinion and gear are given by Addendum circle radii of pinion and gear are given by (i) Velocity of sliding at the point of engagement (vSK): We know that velocity of sliding at the point of engagement K, (ii) Velocity of sliding at the point of disengagement (vSL): We know that the velocity of sliding at the point of disengagement L, (iii) Velocity of sliding at the pitch point (vsP): At the pitch point, the length of path of contact is zero. Therefore, the velocity of sliding at the pitch point is zero. Ans. Example 4.5 Two involute gears of 20° pressure angle are in mesh. The number of teeth on pinion is 20 and the gear ratio is 2. If the pitch expressed in module is 5 mm and the pitch line speed is 1.2 m/s, assuming addendum as standard and equal to one module, find: 1. the angle turned through by pinion when one pair of teeth is in mesh; and 2. the maximum velocity of sliding. Given data: ϕ = 20°; TP = 20; G = 2; m = 5 mm; v = 1.2 m/s; Addendum, aP = aW = 1 module = 5 mm. Solution: 1. Angle turned through by pinion when one pair of teeth is in mesh: Pitch circle radii of pinion and gear are given by Addendum circle radii of pinion and gear are given by Length of the path of contact, KL = KP + PL = 12.65 + 11.5 = 24.15 mm 2. Maximum velocity of sliding: Example 4.6 Two mating involute spur gears of 20° pressure angle have a gear ratio of 2. The number of teeth on pinion is 20 and its speed is 250 revolutions per minute. The module pitch of the teeth is 12 mm. If the addendum of each wheel is such that the path of approach and path of recess on each side are half the maximum possible length, find: (i) addendum for pinion and gear wheel, (ii) the length of arc of contact, and (iii) the maximum velocity of sliding during approach and recess. Assume pinion to be driver. Given data: TP = 20; G = 2; NP = 250 rpm; m = 12 mm Solution: We know that angular velocity of pinion, Pitch circle radii of pinion and gear wheel are given by (i) Addendum for pinion and gear wheel: Given that addendum on pinion and gear is such that the path of approach and recess are half of their maximum possible values, so Substituting the values of R and r in equation (i), we get Substituting the values of R and r in equation (ii), we get (ii) Length of arc of contact: (iii) Maximum velocity of sliding during approach and recess: We know that the velocity of sliding during approach, Similarly the velocity of sliding during recess is given by Example 4.7 The number of teeth on each of the two equal spur gears in the mesh are 40. The teeth have 20° involute profile and the module is 6 mm. If the arc of contact is 1.75 times the circular pitch, find the addendum. [A.U., Nov/Dec 2006] Given data: TP = TG = 40; m = 6 mm; ϕ = 20°; Arc of contact = 1.75 × pc Solution: Given that, Length of arc of contact = 1.75 × circular pitch Since module (m) and number of teeth on pinion (TP) and gear wheel (TG) are same, therefore pitch circle radii of pinion (r) and gear wheel (R) are also same. We know that length of path of contact, In this problem, R = r and RA = rA Example 4.8 A pinion having 20 teeth engages with an internal gear having 80 teeth. If the gears have involute profiled teeth with 20° pressure angle, module of 10 mm and addendum of 10 mm, find the path of contact, arc of contact and the contact ratio. Given data: TP = 20; Internal gearing; TG = 80; ϕ = 20°; m = 10 mm; Addendum, aP = aW = 10 mm Solution: (i) Length of path of contact: Pitch circle radii of pinion and gear wheel are given by Addendum circle radii of pinion and gear wheel are given by For internal gearing, length of path of approach is given by (ii) Length of arc of contact: (iii) Contact ratio:
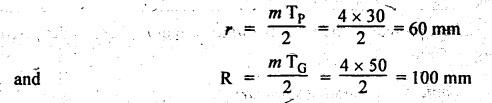


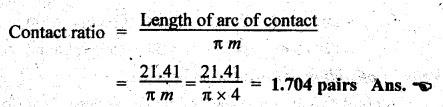

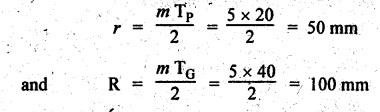
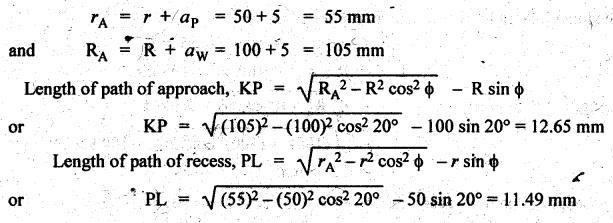

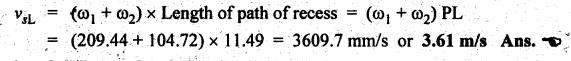
![]()






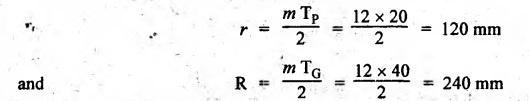


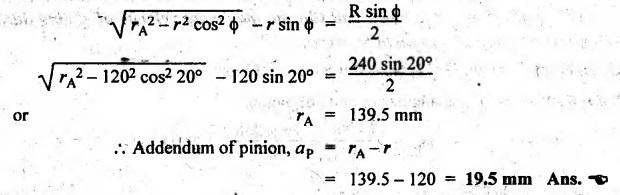

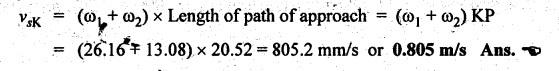



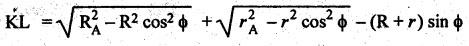






Theory of Machines: Unit II: Gears and Gear Trains : Tag: : Gears and Gear Trains - Theory of Machines - Formulae summary
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
