Transforms and Partial Differential Equations: Unit I: Partial Differential Equations
Formation of partial differential equations by elimination of arbitrary functions
Solved Example Problems
The elimination of one arbitrary function will result in a p.d.e. of the first order. The elimination of two arbitrary functions will result in equations of second order and so on.
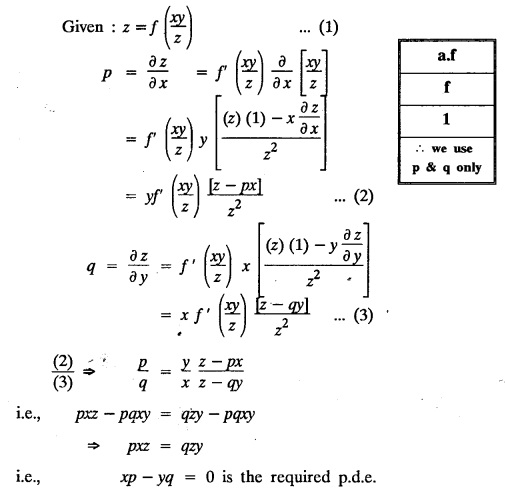
FORMATION OF PARTIAL DIFFERENTIAL EQUATIONS BY ELIMINATION OF ARBITRARY FUNCTIONS Solution: Suppose two functions u & v are connected by the relation Let us eliminate ϕ diff (1) p.w.r. to x and y, we get which, on simplification gives a p.d.e. of the form Equation (5) is a first order p.d.e. linear in p and q. § What can you say about the order of p.d.e. got by eliminating arbitrary functions? Solution: The elimination of one arbitrary function will result in a p.d.e. of the first order. The elimination of two arbitrary functions will result in equations of second order and so on. II. Problems based on Formation of p.d.e. by elimination of arbitrary functions. Example 1.2(a)(1) : Eliminate f from z = f(x2 + y2). Solution: Example 1.2(a)(2) : Eliminate f from z = x + y + f (xy). Solution: Example 1.2(a)(3): Eliminate the arbitrary function f from Solution: Example 1.2(a)(4) : Form the p.d.e. by eliminating ƒ from z = f (x + y). Solution : Example 1.2(a) (5): Eliminate f from z = f(x2 + y2 + z2). Solution: Given: z = f (x2 + y2 + z2) ….(1) ⇒ yp + zpq = xq + zpq yр = xq i.e., yp – xq = 0 which is the required p.d.e. Example 1.2(a)(6) : Eliminate f from z = f (xy/z). Solution: Example 1.2(a)(7) : Eliminate ϕ from xyz = ϕ (x + y + z). Solution: Differentiating (1) p.w.r. to y, we get Example 1.2(a) (8): Find the p.d.e. by eliminating the arbitrary function ϕ from ϕ (x2 + y2) = y2 + z2. Solution: Example 1.2(a) (9) Form the p.d.e. by eliminating f from z = xy + f (x2 + y2 + z2). Solution: Example 1.2(a)(10) Form the p.d.e. by eliminating ϕ from ϕ (x2 + y2 +z2, x + y + z) = 0. Solution: Rewriting the given equation as Example 1.2(a)(11) : Form the p.d.e. by eliminating f from Solution: Example 1.2(a)(12): Obtain p.d.e. from z = f (sin x + cos y). Solution: Example 1.2(a) (13) Form the p.d.e. by eliminating f from Solution: Example 1.2(a)(14) : Form the PDE by eliminating the arbitrary function from Solution: Second Method : Form a p.d.e of eliminating the arbitrary function from Problems based on Formation of p.d.e by elimination of arbitrary functions Example 1.2(b)(1) : Form the p.d.e. by eliminating the arbitrary functions f and ϕ from z = f (x + ct) + ϕ (x — ct). Solution : Example 1.2(b)(2) : Form the p.d.e. by eliminating f and ϕ from z = f(y) + ϕ (x + y + z). Solution: Differentiating (2) p.w.r. to y, we get Example 1.2(b)(3) : Eliminate the arbitrary functions f and g from z= f(x + y) + g(x-iy) to obtain a partial differential equation involving z, x, y. Solution: Example 1.2(b)(4): Form the p.d.e. by eliminating f and ϕ from Solution : Example 1.2(b)(5): Form the differential equation by eliminating the arbitrary functions ƒ and g in z = f (x3 + 2y) + g (x3 − 2y) Solution : which is the required p.d.e. Example 1.2(b)(6) : Form the partial differential equation by eliminating the arbitrary functions f and g in z = x2f(y) + y2 g(x). Solution: which is the required p.d.e. Example 1.2(b) (7): Obtain the partial differential equation by eliminating f and g from z = f(2x + y) + g (3x - y). Solution: Example 1.2(b) (8): Form a partial differential equation by eliminating arbitrary functions from z = xf (2x + y) + g (2x + y). Solution : Differentiating (3) p.w.r. to x, we get Differentiating (3) p.w.r. to y, we get which is the required p.d.e. Form the p.d.e by eliminating the arbitrary functions§ Explain the formation of p.d.e. by elimination of arbitrary functions.
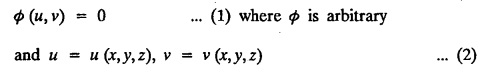

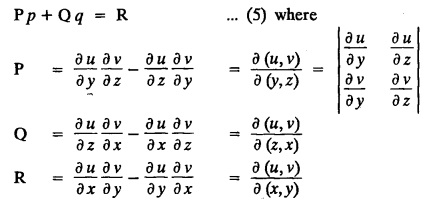


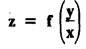 and form a partial differential equation.
and form a partial differential equation.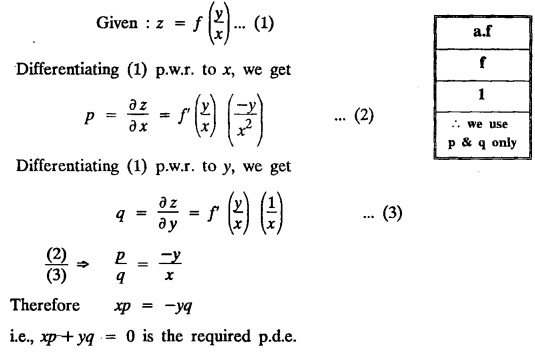
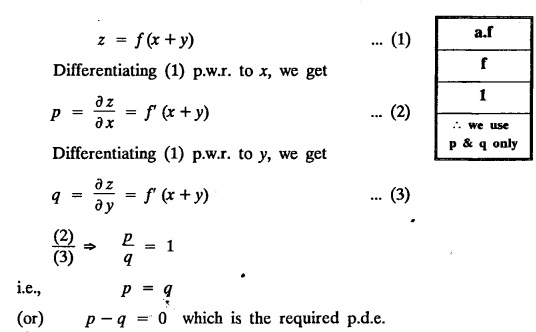
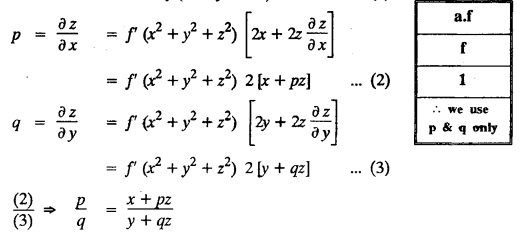
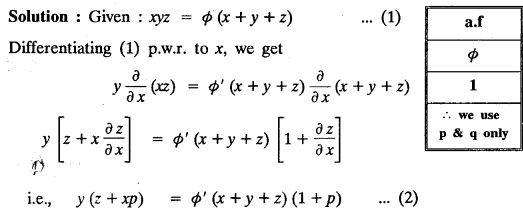
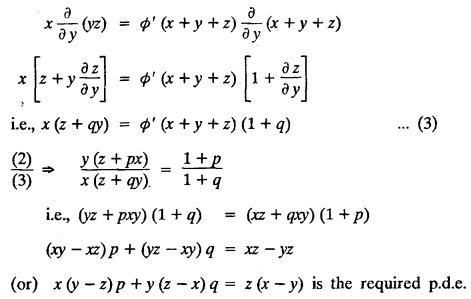


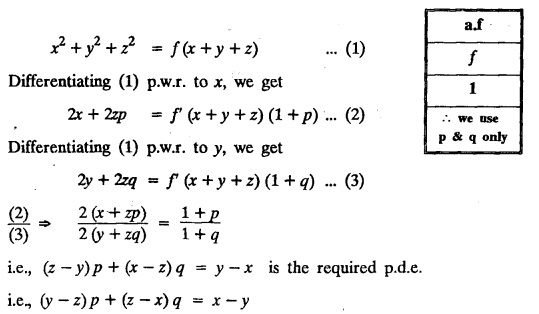
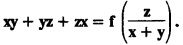

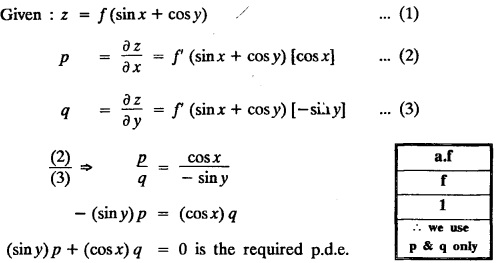
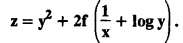

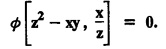

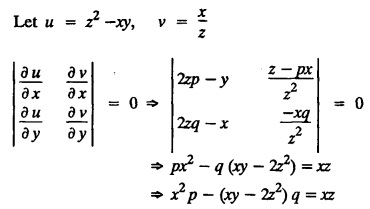
EXERCISE 1.2(a)
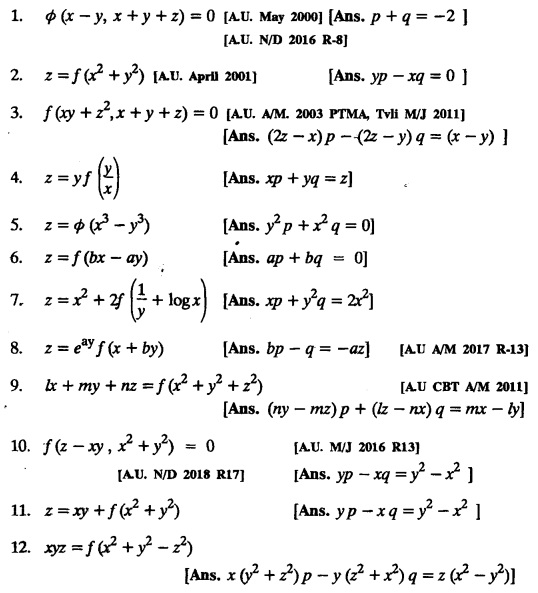
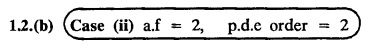
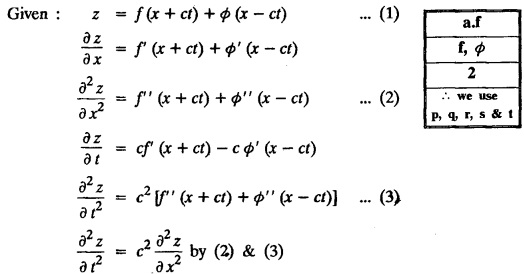
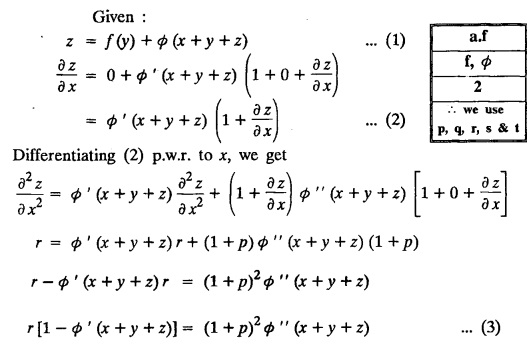

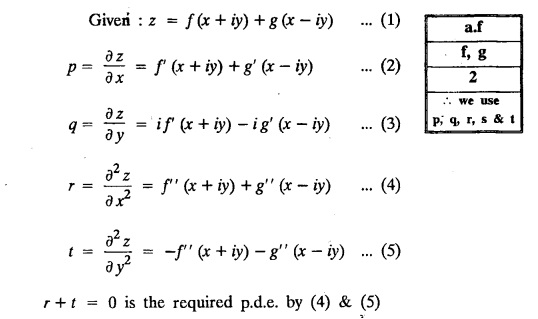
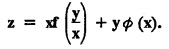
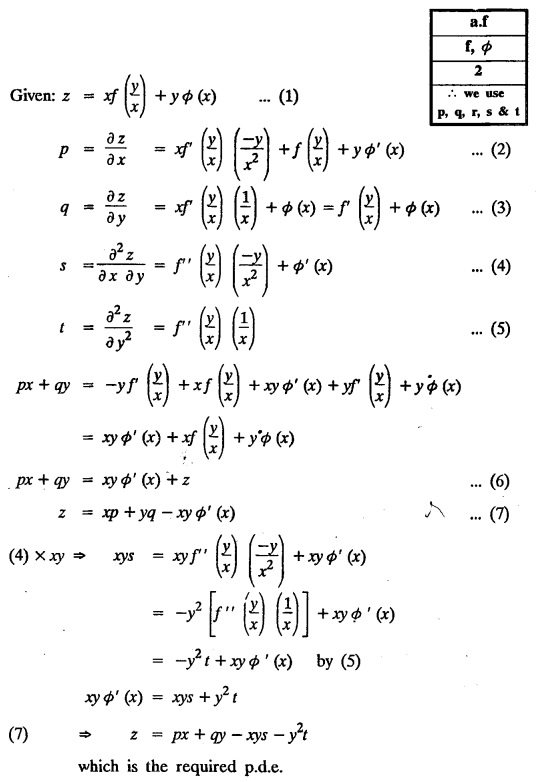

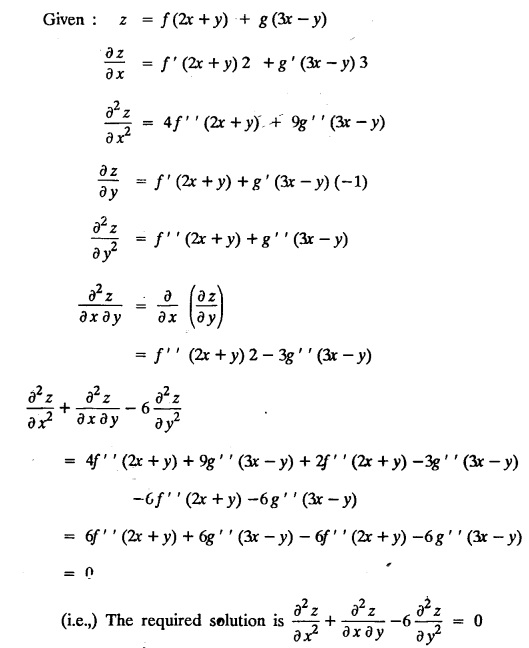
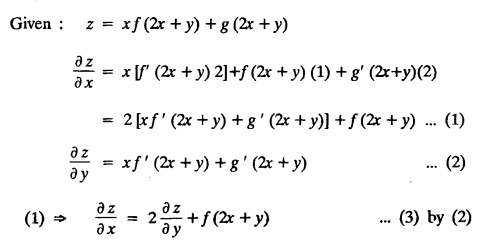
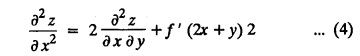
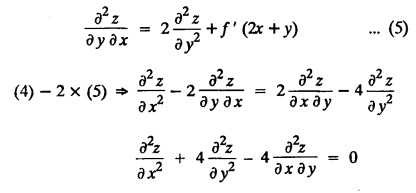
EXERCISE 1.2(b).

Transforms and Partial Differential Equations: Unit I: Partial Differential Equations : Tag: : Solved Example Problems - Formation of partial differential equations by elimination of arbitrary functions
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
