Transforms and Partial Differential Equations: Unit I: Partial Differential Equations
Formation of partial differential equations by elimination of arbitrary Constants
Solved Example Problems
Partial differential equations arise in connection with various physical and geometrical problems.
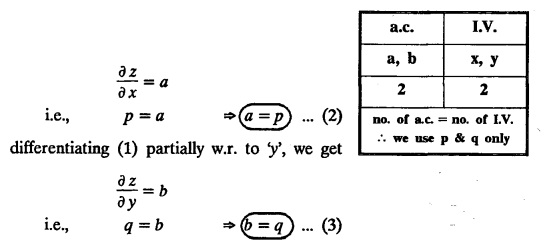
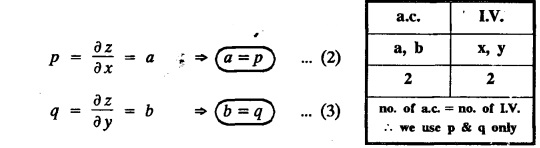
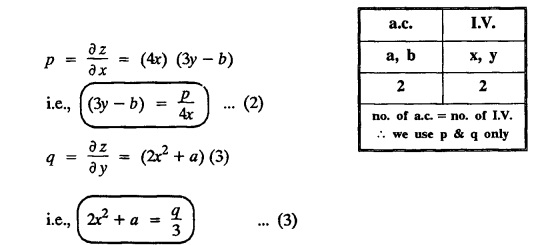
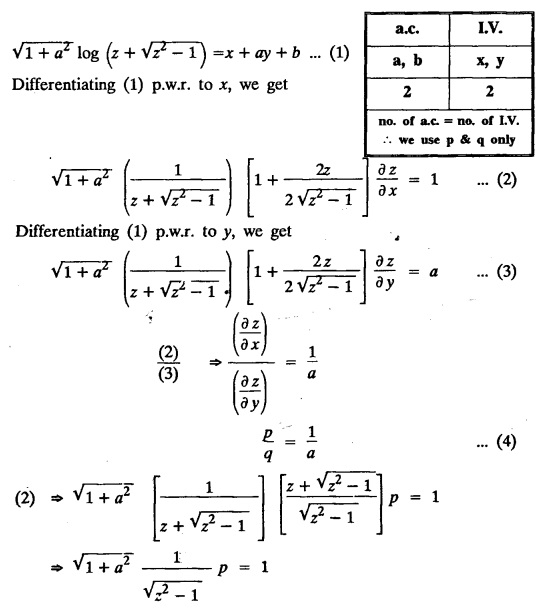
UNIT - I PARTIAL DIFFERENTIAL EQUATIONS Formation on of partial differential equations - Singular integrals - Solutions of Standard types of first order partial differential equations - Lagrange's linear equation - Linear partial differential equations of second and higher order with constant coefficients of both homogeneous and non-homogeneous types. Partial differential equations arise in connection with various physical and geometrical problems. When the functions involved depend on two or more independent variables, usually on time t and one or several space variables. It is fair to say that only the simplest physical systems can be modeled by ordinary differential equations whereas most problems in fluid mechanics, elasticity, heat transfer, electromagnetic theory, quantum mechanics and other areas of physics lead to partial differential equations. Throughout this chapter, we use the following notations: z will be taken as a dependent variable which depends on two independent variables x, y so that z = f(x, y). We write Thus, p + qx = x + y is a partial differential equation of order 1 and r + t = x2 + y is a partial differential equation of order 2. Consider an equation ƒ (x, y, z, a,b) = 0 . ... (1) where a and b denote arbitrary constants. Let z be regarded as function of two independent variables x and y. Differentiating (1) with respect to x and y partially, we get Eliminating two constants a and b from three equations, we shall obtain an equation of the form ϕ (x, y, z, p, q) = 0 which is partial differential equation of the first order. Note 1: In a similar manner, it can be shown that if there are more arbitrary constants than the number of independent variables, the above procedure of elimination will give rise to partial differential equations of higher order than the first. Note 2 : f(x, y, z, a, b) = 0 is called the complete solution of ϕ (x, y, z, p, q) = 0 § Define 'a partial differential equation'. Solution : A p.d.e is one which involves partial derivatives § Define the order of a p.d.e and its degree. Solution: The order of a p.d.e is the order of the highest partial differential coefficient occurring in it. The degree of the highest derivative is the degree of the p.d.e. § When is a p.d.e said to be linear? Solution: A p.d.e is said to be linear, the dependent variable and the partial derivatives occur in the first degree only and separately. § Distinguish between homogeneous and non-homogeneous p.d.e. Solution: An equation of the type The linear differential equations which are not homogeneous, are called non-homogeneous linear equations. § Explain how p.d.e. is formed. Solution: P.d.e. can be obtained (i) by eliminating the arbitrary constants that occur in the functional relation between the dependent and independent variables. (or) (ii) by eliminating arbitrary functions from a given relation between the dependent and independent variables. § What is the essential difference between ordinary differential equation and p.d.e., when both are formed by eliminating arbitrary constants? Solution: The order of an ordinary differential equation will be the same, as the number of constants eliminated. The order of a p.d.e. will be one, in cases, when the number of constants to be eliminated is equal to the number of independent variables. But if the number of constants to be eliminated is more than the number of independent variables, the result of the elimination will, in general, be p.d.e. of second and higher orders. Example 1.1a(2): Eliminate the arbitrary constants a & b from z = ax + by + a2 + b2. Solution: Given z = ax + by + a2 + b2 ….(1) differentiating (1) partially w.r. to 'x', we get ⸫ Substituting (2) & (3) in (1), we get the required p.d.e z = px + qy + p2 + q2 Example 1.1a(3): Form the p.d.e by eliminating the arbitrary constants from z = ax z = ax + by + ab Solution: Given: z = ax + by + ab ……….(1) Substituting (2) & (3) in (1), we get the required p.d.e. i.e., z = px + qy + pq Example 1.1a(4): Form a p.d.e by eliminating the arbitrary constants a and b from z = (x + a)2 + (y − b)2 Solution: Given: z = (x + a)2 + (y − b)2 ….(1) Substituting (2) & (3) in (1), we get 4z = p2 + q2 which is the required p.d.e Example 1.1a(5): Eliminate the arbitrary constants a & b from z = (x2 + a) (y2 + b) Solution: Given: z = (x2 + a) (y2 + b) ...(1) differentiating (1) partially w.r. to 'x', we get i.e., 4xyz = pq which is the required p.d.e Example 1.1a(6) : Form the partial differential equation by eliminating a and b from z = (x2 + a2) (y2 + b2) Solution: Given: Substituting (2) & (3) in (1), we get the required p.d.e. 4 xyz = pq Example 1.1a(7): Form the p.d.e. by eliminating the constants a and b from_ z = axn + byn Solution: Given: z = axn + byn ….(1) Example 1.1a(8): Form a partial differential equation by eliminating the arbitrary constants a and b from the relation z = (2x2 + a) (3y — b). Solution: z = (2x2 + a) (3y − b) ... (1) Substituting (2) & (3) in (1), we get the required p.d.e. Example 1.1a(9) : Form a partial differential equation by eliminating the arbitrary constants from z = a2x + ay2 + b Solution: Example 1.1a(10) : Form the partial differential equation by eliminating a and b from z = a (x + y) + b Solution: From (2) & (3), we get the required p.d.e p = q Example 1.1(a)(11) Form the p.d.e. by eliminating the arbitrary constants a & b from Solution : Example 1.1(a)(12) : Form the partial eliminating a and b from (x − a)2 + (y-b)2 = z2cot2α. Solution : The given equation is which is the required p.d.e. Example 1.1(a)(13) : Obtain partial differential equation by eliminating arbitrary constants a and b from (x- a)2 + (y − b)2 + z2 = 1. Solution: Given: (x − a)2 + (y − b)2 + z2 = 1 ....(1) Here, a and b are the two arbitrary constants. Differentiating (1) p.w.r.to x, we get which is the required p.d.e. Example 1.1(a)(14) : Find the p.d.e. of all planes through the origin. Solution: The general equation to a plane is ax + by + cz + d = 0 ... (1) Differentiating p.w.r.to x, we get Differentiating p.w.r.to y, we get Example 1.1(a)(15): Find the p.d.e. of all sphere whose centres lie on the z axis. Solution: Let the centre of the sphere be (0,0,c) a point on the z axis and k its radius (arbitrary) Here, c & k are arbitrary constants Differentiating (1) p.w.r. to y, we get which is the required p.d.e Example 1.1(a)(16) : Find the p.d.e. of all spheres of radius ‘c' having their centres in the XOY plane. Solution : Let the centre of the sphere be (a, b, 0) a point in the XOY plane, 'c' is the given radius. Differentiating (1) p.w.r. to y, we get Eliminate a, b from (1), (2) & (3), we get Example 1.1(a)(17) : Find the PDE of all planes having equal intercepts on the x and y axis. Solution: Intercept form of the plane equation is Given: a = b [⸪ Equal intercepts on the x and y-axis] Here, a and c are the two arbitrary constants. Differentiating (1) p.w.r. to x, we get Differentiating (1) p.w.r.to y, we get Example 1.1(a)(18) : Form the partial differential equation by eliminating the arbitrary constants a & b from Solution: Example 1.1(a)(19) : Form the partial differential equation by eliminating the arbitrary constants a & b from Solution: Given: Squaring on both sides, we get p2 + q2 + 1 = z2 which is the required p.d.e Example 1.1(a)(20) : Form the p.d.e. by eliminating the arbitrary constants a & b from Solution: Given: Similarly, Differentiating p.w.r. to y, we get Example 1.1(a)(21) : Find the partial differential equation of the family of spheres having their centres on the line x = y = z Solution: General equation of the sphere is (x − a)2 + (y − b)2 + (z − c)2 = k2 Here, centre is (a, b, c) and radius k Centre lies on x = y = z ⇒ a = b = c Equation of sphere is Differentiating (1) p.w.r.to y, we get which is the required p.d.e 1. Form the partial differential equations by eliminating the arbitrary constants a & b 1. z = (x + a) (y + b) [Ans. z = pq] 2. (i) z = ax3 + by3 [Ans. px + qy = 3z ] (ii) z = ax2 + by2 [Ans. px + qy = 2z] 3. z = a2x + b2y + ab [Ans. z = px + qy + √pq ] Example 1.1(b)(1) : Obtain the p.d.e. by eliminating a, b, c from Solution: Differentiating p.w.r. to x, we get Example 1.1(b) (2): Find the differential equation of all spheres whose radii are the same. Sol. The equation of all spheres with equal radius can be taken as (x − a)2 + (y − b)2 + (z − c)2 = k2 …. (1) where a, b, c are arbitrary constants and k is a given constant. Differentiating (1) p.w.r. to x, we get Differentiating (2) p.w.r. to x, we get Differentiating (4) p.w.r. to y, we get which is the required p.d.e Note: The answer is not unique, we can get other equivalent partial differential equations. Example 1.1(b)(3): Form a partial differential equation by eliminating the arbitrary constants a, b & c from z = ax + by + cxy Solution: Note: The answer is not unique, we can get other equivalent partial differential equations. EXERCISE 1.1(b) Form the partial differential equations by eliminating the arbitrary constants a, b, c as the case may be 1. ax + by + cz = 1 [Ans. r = 0 (or) s = 0 (or) t = 0] 2. (x + a)2 + (y + b)2 + c2 [Ans. r = 2 (or) t = 2 (or) s = 0 ]INTRODUCTION
A partial differential equation is one which involves partial derivatives. The order of a partial differential equation is the order of the highest derivative occuring in it.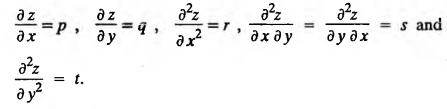
1. FORMATION OF PARTIAL DIFFERENTIAL EQUATIONS BY ELIMINATION OF ARBITRARY CONSTANTS.
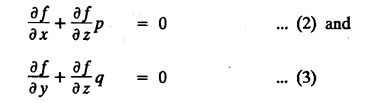
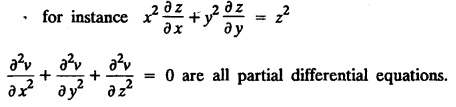
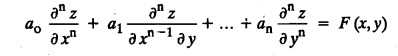 is called a homogeneous linear p.d.e. of nth order with constant co-efficients. It is called homogeneous because all the terms contain derivatives of the same order.
is called a homogeneous linear p.d.e. of nth order with constant co-efficients. It is called homogeneous because all the terms contain derivatives of the same order.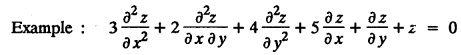

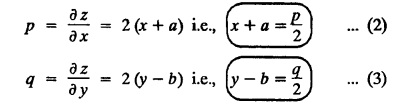
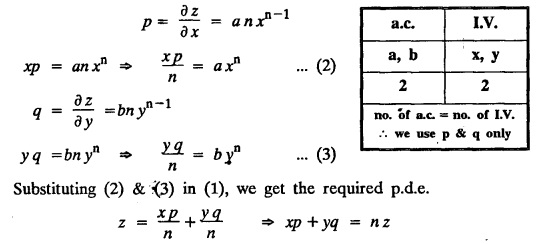
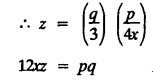
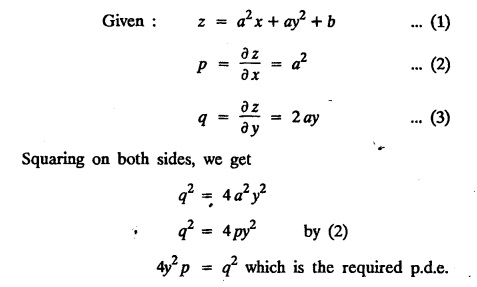
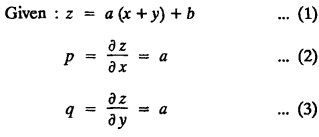

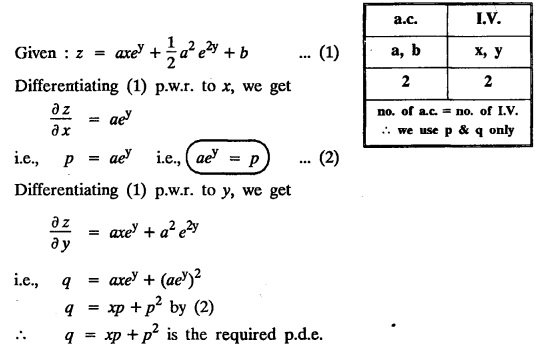

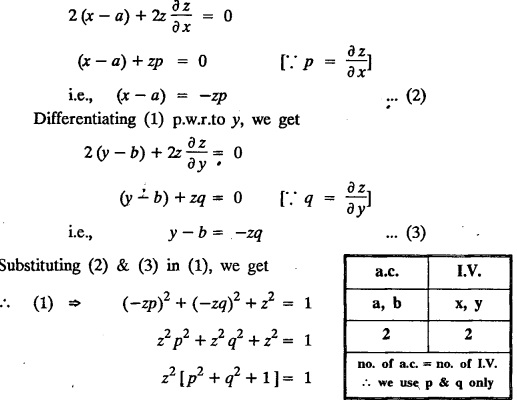
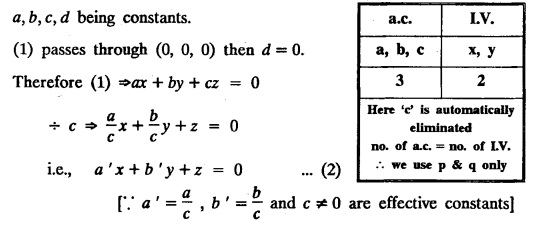
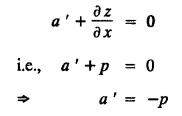
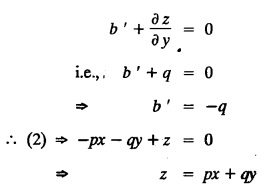
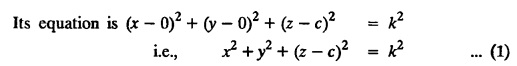
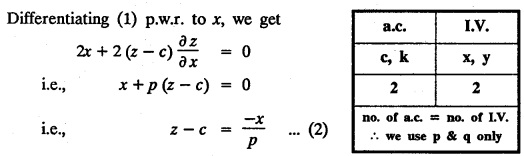
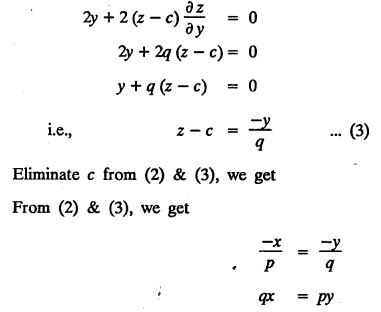
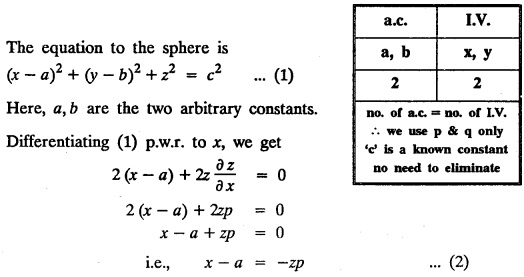
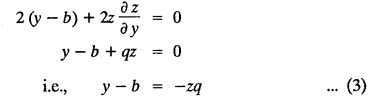
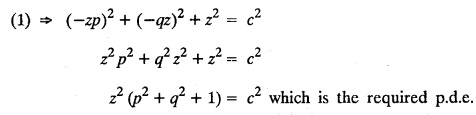
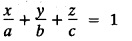

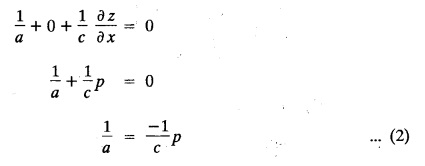
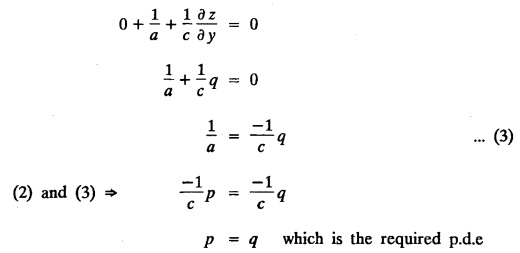
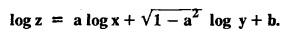

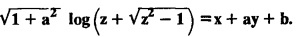
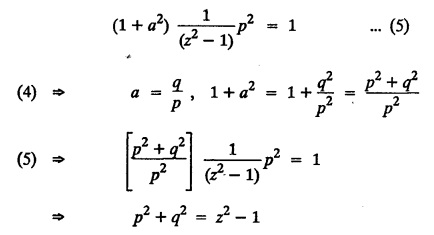
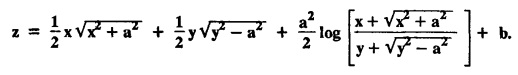

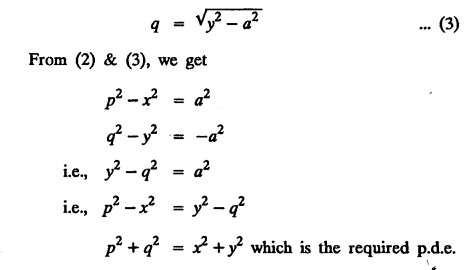
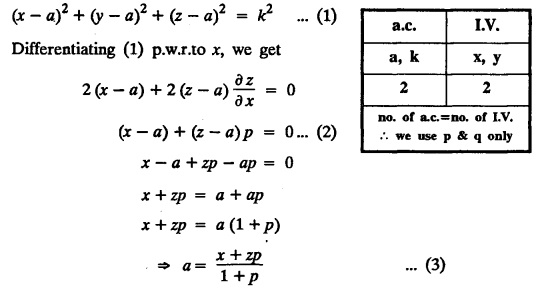
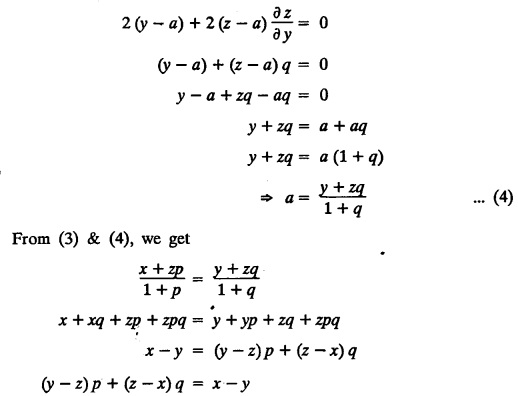
EXERCISE 1.1(a)

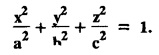
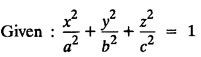


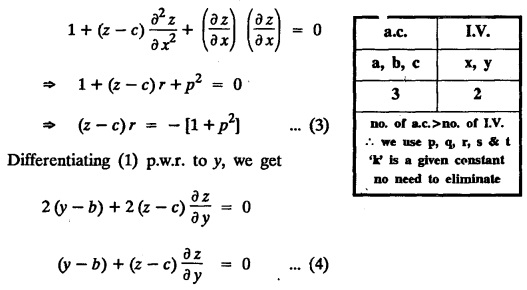

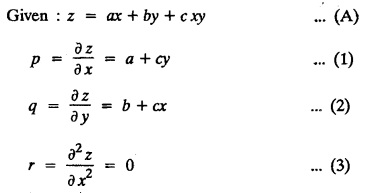
Transforms and Partial Differential Equations: Unit I: Partial Differential Equations : Tag: Form the partial differential equations by eliminating the arbitrary constants a, b, c as the case may be : Solved Example Problems - Formation of partial differential equations by elimination of arbitrary Constants
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
