Engineering Physics: Unit IV: Basic Quantum Mechanics
Extension to Two Dimensions (2D Boxes)
Quantum Mechanics
The solution of one-dimensional potential well is extended for a two-dimensional potential well.
EXTENSION TO TWO DIMENSIONS (2D Boxes) The solution of one-dimensional potential well is extended for a two-dimensional potential well. In a two-dimensional potential well, the particle (electron) can freely move in two directions (say x and y). Therefore, instead of one quantum number n, we have to use two quantum numbers, nx and ny corresponding to the two coordinate axes namely x and y respectively. If a and b are the lengths of the well as shown in fig. 6.11 along x and y axes, then The corresponding normalised wave function of the particle in the two dimensional well is written as From equations (1) and (2), we understand that several combinations of the two quantum numbers (nx and ny) lead to different energy eigen values and eigen functions. Suppose a state has quantum numbers nx =1, ny = 2 Note: Example for particle in two dimensional infinite well is quantum well.
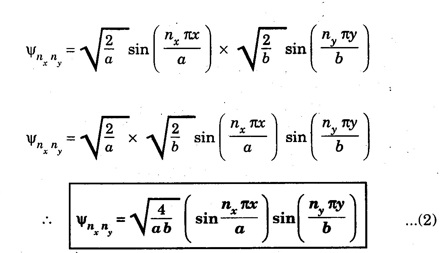
Example

Engineering Physics: Unit IV: Basic Quantum Mechanics : Tag: : Quantum Mechanics - Extension to Two Dimensions (2D Boxes)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
