Engineering Thermodynamics: Unit III: Availability and Applications of II Law
Expressions for energy of an open systems in terms of availability and Thermodynamic second law efficiency
We know that the steady flow energy equation for any kind of open system follows the energy balance concept.
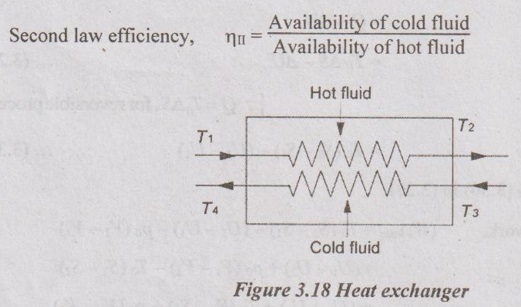
EXPRESSIONS FOR ENERGY OF AN OPEN SYSTEMS IN TERMS OF AVAILABILITY AND SECOND LAW EFFICIENCY We know that the steady flow energy equation for any kind of open system follows the energy balance concept. Case (a): Turbine The following assumptions are made: (i) Potential energies are negligible. (ii) Inlet velocity of the turbine is negligible when compared to exit velocity. Therefore, Steady Flow Energy Equation (SFEE) reduces to m (h1) + Q = m (h2) + W Actual work output, Wact = m (h1 - h2) + Q [⸫ For air, h1 - h2 = Cp (T1 - T2), Q = Negative when the heat is transferred to the surrounding] Reversible work (or) maximum work or availability change, Wmax = (h1 - h2) - To (S1 - S2) ⸫ Irreversibility, I = To ΔS Second law efficiency, Case (b): Compressor/pump The following assumptions are made: (i) Potential energies are negligible. (ii) Kinetic energies are negligible. Therefore, SFEE reduces to m (h1) + Q = m (h2) + W Actual work output, W = m (h1 - h2) + Q Compressor work is negative because it is supplied to perform the action. [⸪ Compressor/ pumps are work absorbing devices] Maximum work input, Wmax = (h1 - h2) - To (S1 - S2) Case (c): Heat exchanger Consider my kg of hot fluid with a specific heat of C1 exchanging heat with a cold fluid of m2 kg with a specific of C2. By heat balance, ⸫ Heat gained by cold fluid = Heat given out by hot fluid m2 C2 (T4 - T3) = m1 C1 (T1 - T2) Availability of cold fluid, Bc = m2 C2 (T4 - T3) = To C1 (S4 – S3) Availability, of Hot fluid, Bh = m1 C1 (T1 - T2) - To (S1 - S2) Irreversibility, I = Bh - Bc Case (d): Throttling process For throttling process, Enthalpy before throttling = Enthalpy after throttling h1 = h2 For throttling process, both work output and heat transfer are zero. ⸫ Maximum work, Wmax = (h1 - h2) - To (S1 - S2) So, maximum work, Wmax = To (S2 - S1) = ψ1 – ψ2 where ψ1 = Availability at inlet and ψ2 = Availability at outlet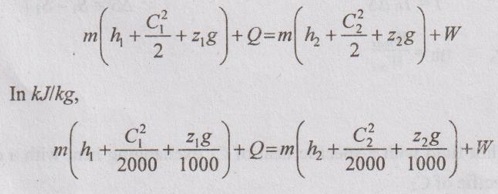
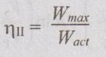
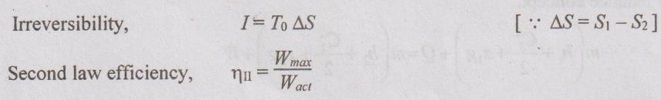
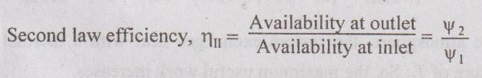
Engineering Thermodynamics: Unit III: Availability and Applications of II Law : Tag: : - Expressions for energy of an open systems in terms of availability and Thermodynamic second law efficiency
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
