Engineering Thermodynamics: Unit III: Availability and Applications of II Law
Expressions for energy of a closed systems in terms of availability and Thermodynamic second law efficiency
Consider air heated from the temperature of T1 to T2 at constant volume and also heat transfer with the surrounding at To.
EXPRESSIONS FOR ENERGY OF A CLOSED SYSTEMS IN TERMS OF AVAILABILITY AND SECOND LAW EFFICIENCY Case (a): Constant volume process Consider air heated from the temperature of T1 to T2 at constant volume and also heat transfer with the surrounding at To. Total heat energy supplied to air, Q = m Cv (T2 - T1) Available energy, A.E = Q - To ΔS where ΔS = m Cv In (T2 / T1) Unavailable energy, U.A.E = Q - A.E U.A.E = m Cv (T2 - T1) - [m Cv (T2 - T1) - To ΔS] = To ΔS Case (b): Constant pressure process If air is heated from T1 to T2 with the surrounding at the temperature of To, Heat energy supplied, Q = m Cv (T2 - T1) Available energy, A.E = Q - To ΔS Where ΔS = m Cp In (T2 / T1) Unavailable energy, U.A.E = Q - A.E U.A.E = m Cp (T2 - T1) - [m Cp (T2 - T1) - To ΔS] = To ΔS Case (c): Constant temperature or isothermal process Heat energy, Q = p1v1 In (p1 / p2) Available energy, A.E = Q - To ΔS ΔS = Q/T1 or Q/T2 Unavailable energy, U.A.E = To ΔS Case (d): Polytropic process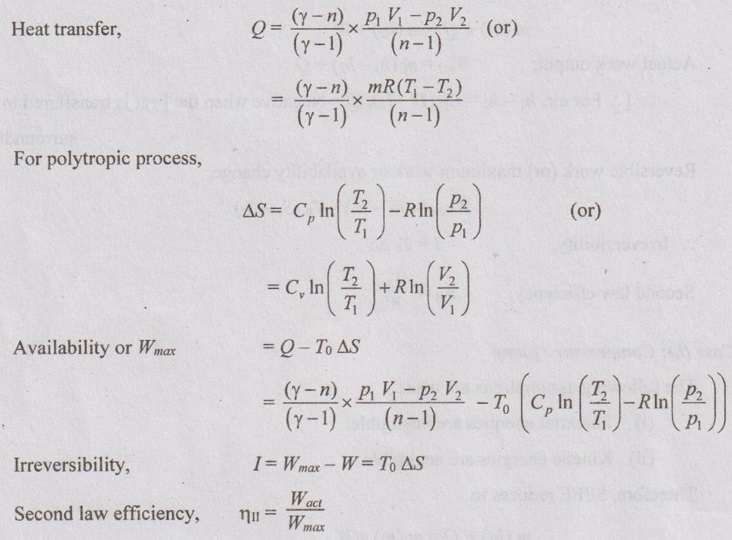
Engineering Thermodynamics: Unit III: Availability and Applications of II Law : Tag: : - Expressions for energy of a closed systems in terms of availability and Thermodynamic second law efficiency
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
