Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies
Equilibrium of Three Forces in a Plane
When an object is in equilibrium under the action of three forces which are not parallel, then the three forces must be concurrent.
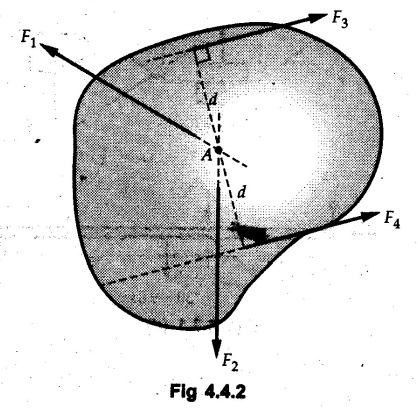
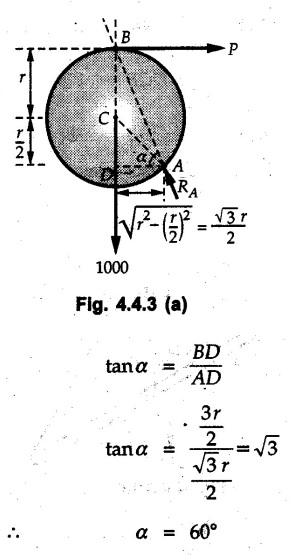
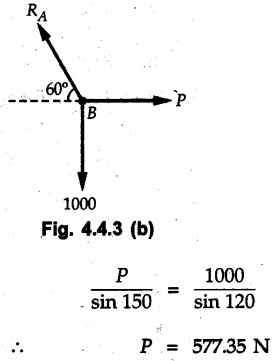
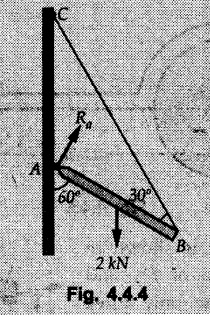
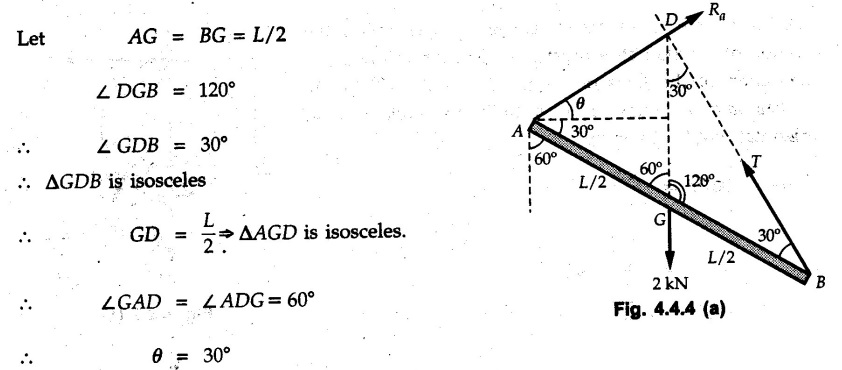
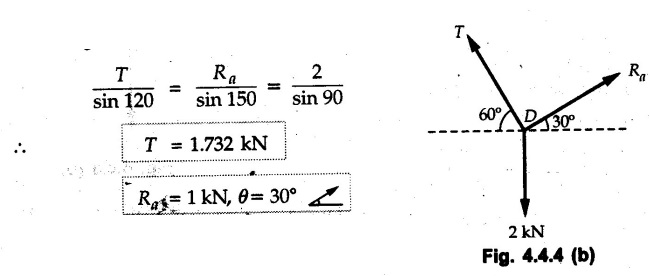
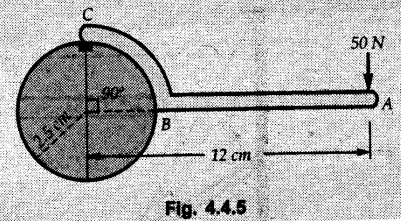
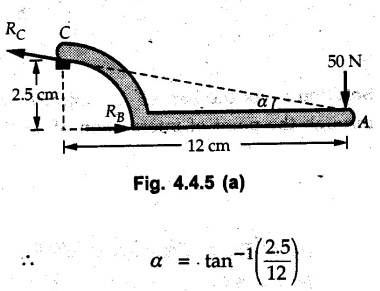
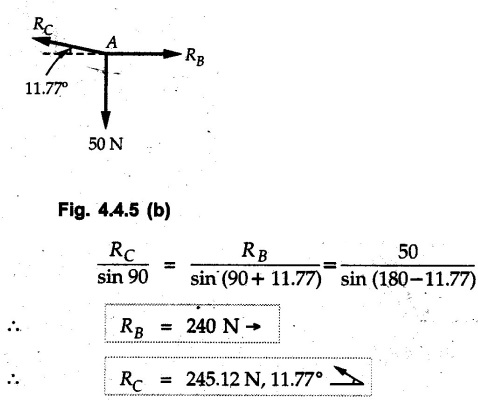
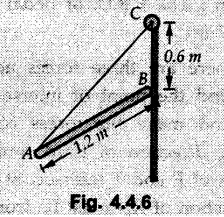
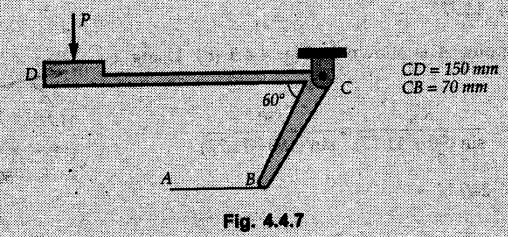
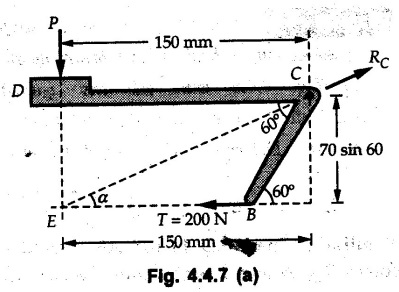
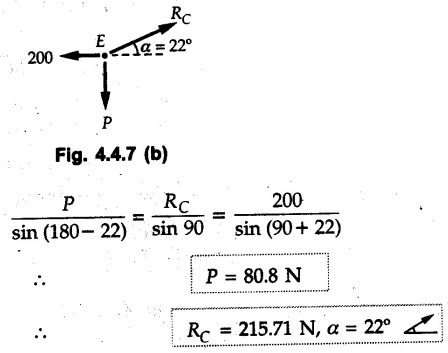
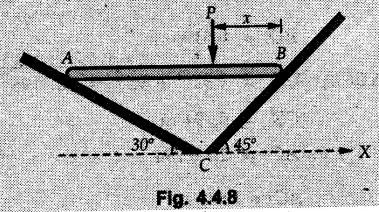
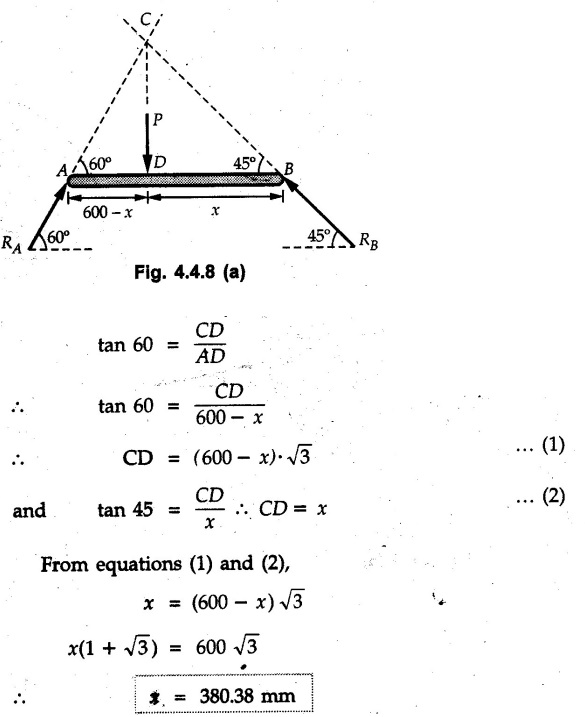
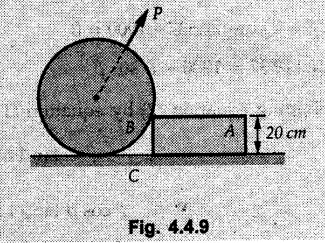
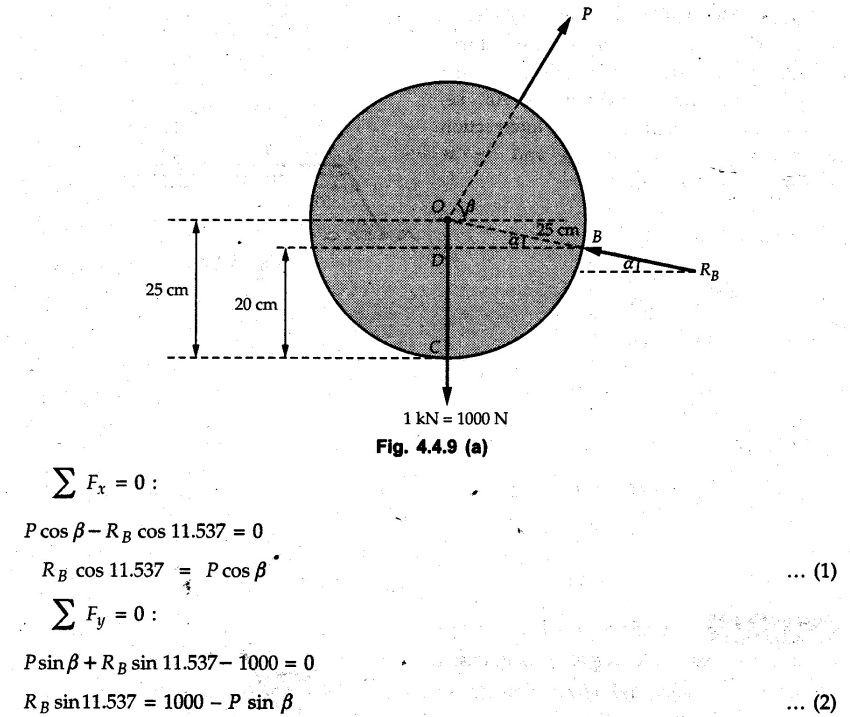
Equilibrium of Three Forces in a Plane • When an object is in equilibrium under the action of three forces which are not parallel, then the three forces must be concurrent. • If two forces F1 and F2 are not parallel, their lines of action will intersect at some point A as shown in Fig. 4.4.1. • If line of action of the third force F3 does not pass through A, the combined moment of all the forces about A will be non-zero and the object will not remain in equilibrium. Hence, for equilibrium of the object, the forces must be concurrent. • Note that this condition is applicable only for three non-parallel forces. • For more than three forces, the moment of F3 about A can be nullified by moment of F4 about A without the force system becoming concurrent as shown in Fig. 4.4.2. • Procedure : If two out of three forces are not parallel, then 1) Find the point of intersection of the lines of action of the two forces. 2) Draw the line of action of the third force through the point of intersection of first two and use this to find direction of the third force (i.e., its angle with horizontal). 3) Use Lami's theorem as the three concurrent forces are in equilibrium. Example 4.4.1 A roller of radius r and weight W = 1000 N is to be pulled over a curb of height h = r/2 as shown in Fig. 4.4.3 by applying a horizontal force P at the end of a string wound around. the circumference of the roller. Find the magnitude of force P required to start the roller over the curb. Solution: The F.B.D. of roller is shown in Fig. 4.4.3 (a). To pull the roller over the curb, the reaction at the bottom surface tends to zero. As there are three forces acting on the roller, the direction of reaction at A must pass through the point of intersection of the lines of action of P and 1000 N. As RA has line of action from A to B, its angle α with horizontal will be given by As the forces are concurrent at B as shown in Fig. 4.4.3 (b). Using Lami's theorem, Example 4.4.2 A prismatic bar AB of weight 2 kN is hinged to a vertical wall at 'A' and supported at B by a cable BC. Determine the magnitude and direction of the reaction Ra at the hinge A and the tensile force in the cable 'BC'. Refer Fig. 4.4.4. Solution: As the bar AB is subjected to three forces the line of action of Ra must pass through the point of intersection of 2 kN and T as shown in Fig. 4.4.4 (a). The F.B.D. of point D is shown in Fig. 4.4.4 (b). Using Lami's theorem, Example 4.4.3 Determine the forces exerted on the cylinder at B and C by the spanner shown in Fig. 4.4.5 due to a vertical force of 50 N applied to the handle, Solution: The F.B.D. of spanner is shown in Fig. 4.4.5 (a). The line of action of Rg and 50 N intersect at A. As there are only three forces acting on the spanner, the line of action of RC must pass through pass through point A for equilibrium of spanner as shown in Fig. 4.4.5 (a) ⸫ α = 11.77° The F.B.D. of point A is shown in Fig. 4.4.5 (b). Using Lami's theorem, Example 4.4.4 A 1.2m long rod of uniform cross-section, is held in equilibrium as shown in Fig. 4.4.6 with one end against a frictionless wall and the other end attached to the cord. Determine the length of the cord. Solution: The F.B.D. of rod AB is shown in Fig. 4.4.6 (a). The rod subjected to three forces RB, W and T which must be concurrent at point D on the cord. ΔADG and ΔACB are similar. Example 4.4.5 The required tension in cable AB is 200 N. Find a) The vertical force P which must be applied to the pedal, and b) The reaction at C. Refer Fig. 4.4.7. Solution: The F.B.D. of pedal is shown in Fig. 4.4.7 (a). As there are three forces acting on the pedal, find the point of intersection of two forces and make the forces concurrent by choosing direction of third force. The lines of action of P and T intersect at E. Therefore line of action of RC must be from E to C. Using Lami's theorem at E (Fig. 4.4.7 (b)), Example 4.4.6 A light beam AB of 600 mm length is resting against smooth inclined planes AC and CB making angles 30° and 45° respectively to X-axis. In the horizontal position as shown in Fig. 4.4.8, obtain position of load P i.e. distance 'x' for equilibrium. Solution: The F.B.D. of AB is shown in Fig. 4.4.8 (a). As there are three non-parallel forces acting on AB, they must be concurrent for equilibrium of AB. i.e, P must pass through point of intersection of the lines of action of RA and RB as shown in Fig. 4.4.8 (a). Example 4.4.7 A uniform wheel of 50 cm diameter and 1 kN weight rests against a rigid rectangular block of thickness 20 cm. Considering all surfaces smooth, determine i) Least pull to be applied through the centre of wheel to just turn it over the corner of block ii) Reaction of block. Solution : The F.B.D. of wheel is shown in Fig. 4.4.9 (a). For the limiting condition of equilibrium, the three forces must be concurrent. Hence the reaction at B must pass through the point of intersection of the weight and force P, i.e., through the centre O of the wheel. From ΔODB; ⸫ α = 11.537 ° Dividing equation (2) by equation (1), we get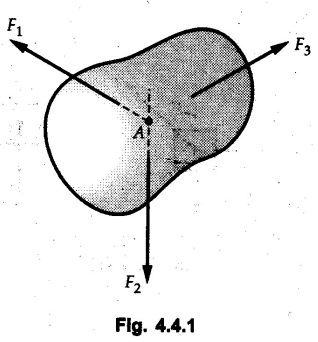
Solved Examples for Understanding


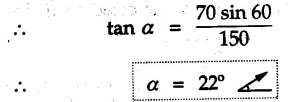
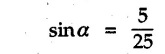

Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies : Tag: : - Equilibrium of Three Forces in a Plane
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
