Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies
Equilibrium of a Rigid Body in Space
with Solved Example Problems
For a non-concurrent general force system in equilibrium, the resultant force and the resultant moment about any point is zero.
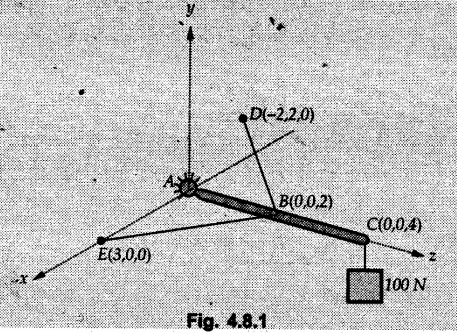
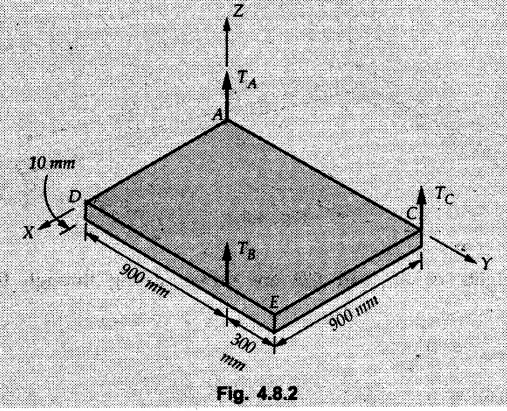
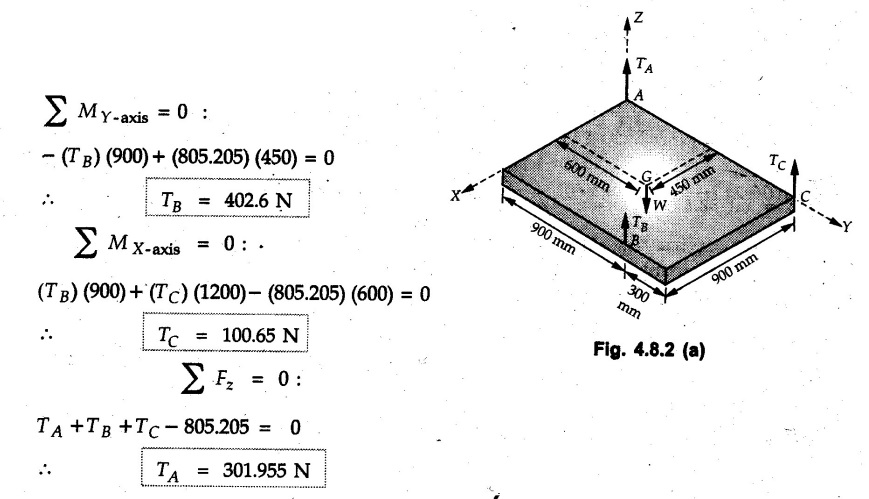
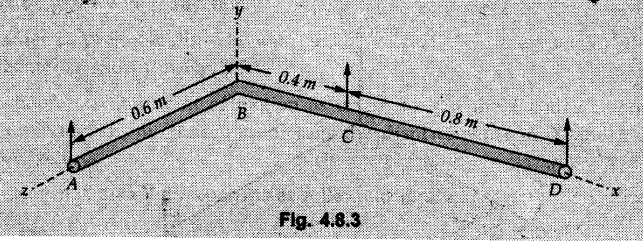
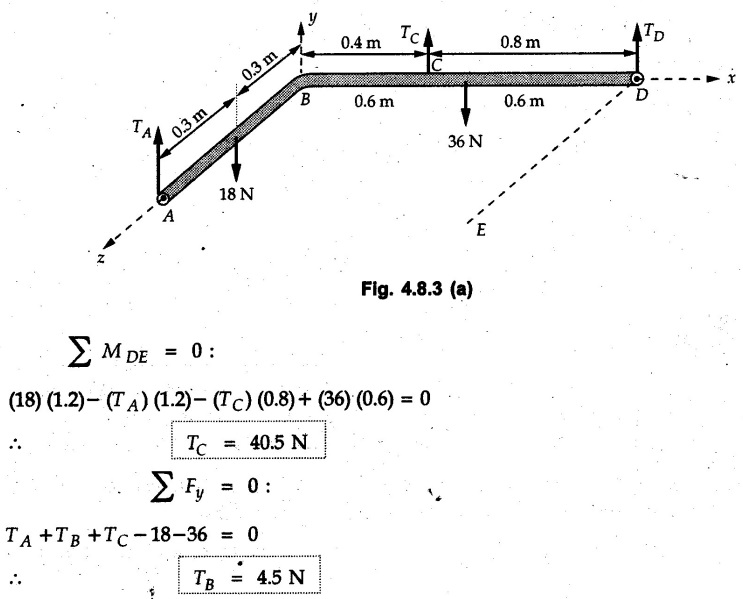
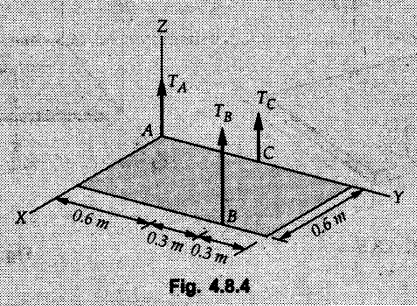
Equilibrium of a Rigid Body in Space • For a non-concurrent general force system in equilibrium, the resultant force and the resultant moment about any point is zero. • As moment about a point is a vector in three dimensions, we get three equations by equating moment to zero. • Thus six equations can be obtained which can be solved for six unknowns. • For equilibrium of parallel force system, one of the equations can be obtained by equating summation of all forces, along an axis parallel to the forces to zero. • Additional equations can be obtained by equating moments of all forces about different lines in a plane perpendicular to the forces to zero. Example 4.8.1 Determine tensions is cords BD and BE which hold a rigid light member in horizontal position as shown. Assume A as ball and socket joint. Solution: The unknown reactions at A can be avoided in equations by taking moment about A. Example 4.8.2 A plate ACED weighs 7,600 kg/m3. It is held in horizontal plane by three wires at A B and C. Find tensions in the wires. Refer Fig. 4.8.2. Solution: The weight of the plate is W = ρ × g × Volume = 7600 × 9.81 × 0.9 × 1.2 × 10 × 10-3 ⸫ W = 805.205 N It acts through the C.G. shown in Fig. 4.8.2 (a). Example 4.8.3 Fig. 4.8.3 shows steel pipe ABCD of length 1.8 m having 90° bend at B. The pipe weights 30 N/m and supported by three vertical wires attached to the pipe at A, C and D. Find tension in wires. Solution: The weights of AB and CD are shown acting through their centres in Fig. 4.8.3 (a). Consider moments about a line DE parallel to z-axis. Example 4.8.4 The uniform concrete slab has a weight of 5500 N. Determine tension in each of the three parallel supporting cables when the slab is held in horizontal plane as shown in Fig. 4.8.4. Solution: Weight of slab acts at its centre ⸫ (TB) (0.6) + (5500) (0.3) = 0Solved Examples for Understanding

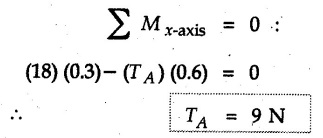
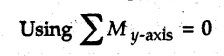

Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies : Tag: : with Solved Example Problems - Equilibrium of a Rigid Body in Space
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
