Theory of Machines: Unit III: Friction in Machine Elements
Equilibrium of a body on an inclined plane
Motion of the Body Up the Plane
The inclined plane is very frequently used in one form or the other.
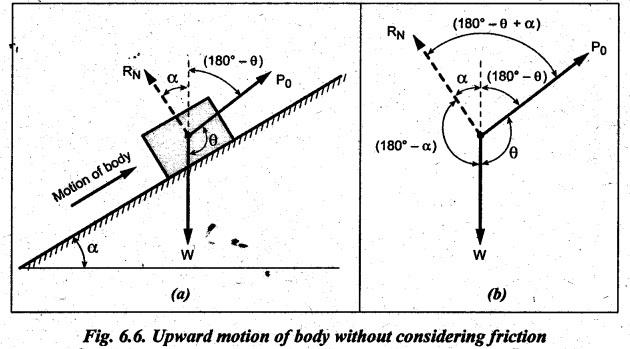
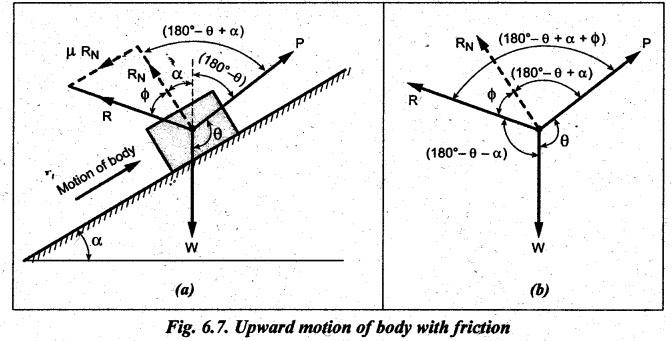
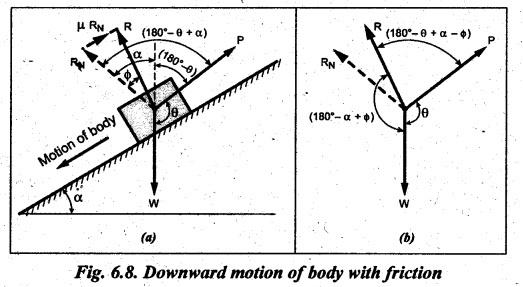
EQUILIBRIUM OF A BODY ON AN INCLINED PLANE The inclined plane is very frequently used in one form or the other. So, it is necessary to examine the various forces acting on a body when it moves up or down the plane. (a) Without considering friction: Consider the body resting on the inclined plane as shown in Fig.6.6(a). Let the external force P0 is applied to move the body upwards. Let W = Weight of the body, α = Angle of inclination of the plane to the horizontal, ϕ = Limiting angle of friction for the contact surfaces, P0 = Effort required to move the body up the plane neglecting friction, P = Effort applied to move the body up the plane considering friction, θ = Angle which the line of action of P makes with the weight of the body W, μ = Coefficient of friction between the surfaces of the plane and the body, RN = Normal reaction, and R = Resultant reaction. The body is in equilibrium under the following three forces, as shown in Fig.6.6(a): (i) Weight of the body W, (ii) Normal reaction RN, and (iii) External effort P0. The free body diagram (FBD) of forces is shown in Fig.6.6(b). Applying Lami's theorem for Fig.6.6(b), we get (b) With considering friction: When friction is taken into account, a frictional force F = μ RN acts in the direction opposite to the motion of the body, as shown in Fig.6.7(a). Due to friction, the effort required to tend to move the body up the plane is increased from P0 to P. The resultant reaction R is inclined at angle ϕ with the normal reaction RN. The FBD of forces is shown in Fig.6.7(b). Now applying Lami's theorem for Fig.6.7(b), we get (a) Without considering friction: Consider the body moving downwards without friction. Since the frictional force is not to be taken into account, there will be same three forces: (i) Weight (W), (ii) Normal reaction (RN), and (iii) Effort (P0), under which the body will be in equilibrium position. Hence when friction is neglected, equation (6.6) of article holds true. (b) With considering friction: When the friction is taken into account, the force of friction F = μ RN will act up the plane and the resultant reaction R will make an angle ϕ with RN towards its right, as shown in Fig.6.8(a). The FBD of forces is shown in Fig.6.8(b). Now applying Lami's theorem, for Fig.6.8(b), we get1. Motion of the Body Up the Plane


2. Motion of the Body Down the Plane
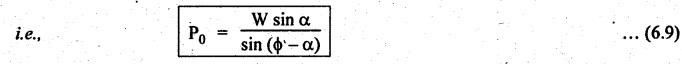

Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Motion of the Body Up the Plane - Equilibrium of a body on an inclined plane
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
