Theory of Machines: Unit III: Friction in Machine Elements
Equilibrium of a body on a horizontal plane
Friction in Machine Elements - Theory of Machines
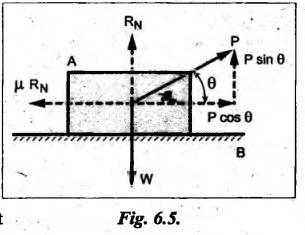
Suppose a body A of weight (W) is resting on a horizontal plane B, as shown in Fig.6.4.
EQUILIBRIUM OF A BODY ON A HORIZONTAL PLANE Suppose a body A of weight (W) is resting on a horizontal plane B, as shown in Fig.6.4. Let a tractive force P is applied at an angle θ with the horizontal, the body A just tends to move. The active forces on the body A are: (i) Weight, W, and (ii) Tractive force or effort, P. The reactive forces are: (i) Normal reaction, RN, and (ii) Frictional force, F. Thus, external forces acting on the body A are: Vertical: (i) (W − P sin θ) ↓ (downwards) (ji) RN ↑ (upwards) Horizontal: (i) P cos α → (towards right) (ii) F = μ • RN← (towards left) For satisfying the equilibrium conditions, ΣFV = 0 and Σ FH = 0 or P cos θ cos ϕ = W sin ϕ - P sin θ • sin ϕ or P (cos θ • cos ϕ + sin θ sin ϕ) = W sin ϕ The value of P is minimum when cos (θ - ϕ) is maximum, so Hence, the effort P will be minimum if its angle of inclination & with the horizontal is equal to the angle of friction ϕ. Example 6.1 The force required to pull a body of weight 50 N on a rough horizontal plane is 15 N. Determine the coefficient of friction, if the force is applied at an angle of 15° with the horizontal. Given data: W = 50 N; P = 15N, θ = 15°. Solution: The body is in equilibrium under the action of the forces, as shown in Fig.6.5. Resolving the forces horizontally, we get F = μ RN = 15 cos 15° ... (i) Now, resolving forces vertically, we get RN + 15 sin 15° = W = 50 ⸫ RN = 50 - 15 sin 15° = 46.12 N Substituting the value of RN in equation (i), we get μ × 46.12 = 15 cos 15° or μ = 0.314 Ans. 


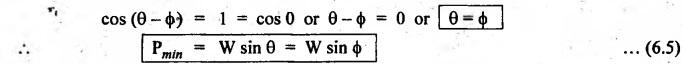
![]()
Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Friction in Machine Elements - Theory of Machines - Equilibrium of a body on a horizontal plane
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
