Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Equations of state for Real Gas
The scientist Van der Waals considered these two corrections to analyse the behaviour of real gases during 1879.
EQUATIONS OF STATE FOR REAL GAS The scientist Van der Waals considered these two corrections to analyse the behaviour of real gases during 1879. ⸫ The equation of state for real gases is given by For ideal gas, the constants a and b are zero. The values of a and b are dependent on the type of fluid or gases used. If molar volume is considered in the analysis, the equation of state becomes Van der Waals equation has some limitations as follows: 1. The study had not been made closely under actual conditions and its validity bias failed. 2. The values of a and b are assumed to be constant but they will vary with temperature which is experimentally found. 3. At critical point, Van der Waals equation becomes This equation is based on five experimentally determined constraints in the form of The Beattie-Bridgeman equation is known to be reasonably accurate for densities values up to 0.8ρcr, where ρcr is the density of the substance at critical point. The equation of state is expressed as It can take up substances at densities up to about 2.5 ρcr. Virial or virtual expansions are only applicable to gases of low and medium densities. The equation state of a substance is given by The coefficient of a(T), b(T), c(T), d(T) are virial coefficients. The virial coefficient will vanish when the pressure becomes zero. Finally, the equation of state reduces to the ideal-gas equation. 1. Berthelot equation of state: 2. Dieterici equation of state: where a and b are constants p = Pressure, Pa v = Volume, m3 R = Gas constant, J/kgK T = Temperature, K.1. Van der Waals equation:
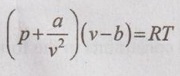

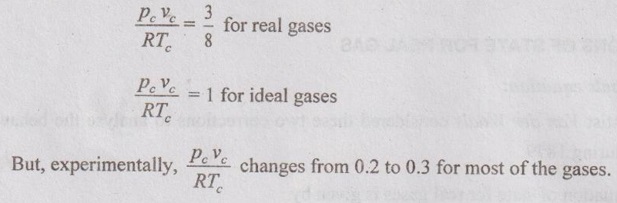
2. Beattie-Bridgeman equation of state:
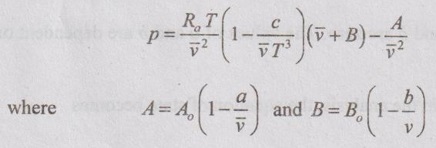
3. Benedict-Webb-Rubin equation of state:
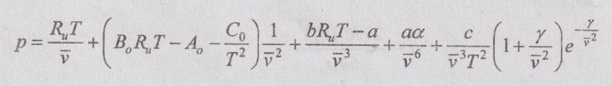
4. Virial equation of state:
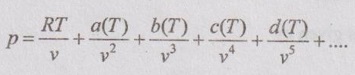
5. Berthelot and Dieterici equations of state:
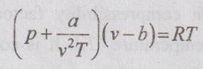
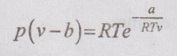
Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : - Equations of state for Real Gas
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
